Как вычислить объем жидкости в цилиндрическом сосуде
Продолжая тему, начатую тут Объем жидкости в цилиндрической таре и в ответ на запрос Прошу помочь с расчётом публикуем калькулятор, вычисляющий объем жидкости в цилиндрической емкости под наклоном.
Для вычисления вам потребуется ввести параметры емкости (радиус и длину) замерить уровень жидкости вблизи от одного из оснований и угол наклона.
Замер уровня жидкости
Замер уровня жидкости должен производиться в диаметральной плоскости емкости перпендикулярно нижней цилиндрической стенке (см. рисунок), непосредственно у одного из оснований или на некотором расстоянии от него ( в этом случае надо заполнить параметр «Расстояние от основания при измерении»). Как вариант замера, в случае небольшого количества жидкости и если есть возможность наклонить емкость, можно наклонить ее таким образом, чтобы уровень у верхнего основания был нулевым. Тогда надо замерить только расстояние от верхнего основания до границы начала жидкости. Если же наклонить бочку так, что жидкость будет подходить ровно к верхнему углу (месту смыкания верхнего основания и боковой поверхности емкости) то уровень и расстояние до основания будут нулевыми, замерить потребуется только угол.
Детали и формулы расчета можно найти непосредственно под калькулятором.
Объем жидкости в наклонной цилиндрической таре
Расстояние от ближайшего основания при измерении уровня жидкости. (0 если измерение происходило непосредственно у основания).
Точность вычисления
Знаков после запятой: 2
Уровень жидкости у верхнего основания
Уровень жидкости у нижнего основания
Длина частично заполненной части
Длина полностью заполненной части
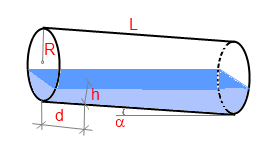Наклоненная цилиндрическая емкость
Готовой формулы для вычисления объема жидкости в наклонной емкости мне найти не удалось, поэтому пришлось ее выводить.
Если одно основание емкости заполнено полностью, то весь объем жидкости можно условно разделить на две части:
- цилиндрическая часть, объем которой находится тривиально по формуле объема цилиндра см. Цилиндр
- часть цилиндра усеченная под углом поверхностью воды. Объем этой части найти также не трудно по той же формуле, деленной пополам, если жидкость не доходит до верхнего основания (емкость стоит почти вертикально).
Формулы для вычисления объема частично заполненной части емкости
Сложности начинаются, если жидкость частично закрывает одно или оба основания, так как на рисунке.
Для вычисления объема такого тела мы заметим, что любое сечение этого тела перпендикулярно длине емкости представляет собой Сегмент круга. Тогда объем этого тела можно записать, как определенный интеграл по площади сегмента в зависимости от длины фигуры:
где -функция зависимости угла сегмента от длины фигуры x,
которая выражается следующим образом:
где
a — угол наклона емкости,
h0 — уровень жидкости у верхнего основания цилиндра (длина погруженной части верхнего основания) см. раздел Замер уровня жидкости
Подставим в формулу объема это выражение и упростив его получим полную формулу объема:
где
Вычислив интеграл, получаем:
где ,
Определение длины частично заполненной части
Приведенные выше формулы справедливы для следующих предположений:
- Оба основания заполнены частично
- Уровень жидкости h0 измерен непосредственно у верхнего основания с учетом наклона. (Фактически h0 – это длина погруженной части верхнего основания см. раздел Замер уровня жидкости).
- Нет полностью пустых или полностью заполненных частей цилиндра.
Но калькулятор может принимать на вход значения уровня жидкости, измеренные на некотором расстоянии от верхнего либо от нижнего основания. Допускаются полностью пустые и полностью полные части цилиндрической емкости.
Чтобы вычислить уровень жидкости у верхнего основания hu используйте формулы:
где hll – уровень жидкости, измеренный на расстоянии ll от нижнего основания, Lc – длина емкости
где hlu – уровень жидкости, измеренный на расстоянии lu от верхнего основания.
Если уровень huравен или больше нуля, мы считаем h0=hu, и Lf = Lc.
Пустая часть бака
В противном случае hu может быть отрицательным. Это означает, что какая-то часть бака пуста. В этом случае мы полагаем h0=0 и вычисляем длину оставшейся (заполненной) части цилиндра: Lf по формуле:
где Lc – длина цилиндра.
Полностью заполненная часть
Уровень жидкости у нижнего основания h1 можно определить следующим образом:
Если вычисленно значение h1 больше диаметра цилиндра, то некоторая часть цилиндра – заполнена полностью. Чтобы вычислить длину этой части мы используем формул:
Объем этой части посчитать тривиально: Цилиндр
После этих вычислений мы можем подставить длину частично заполненной части и уровень жидкости h0 в формулы первого раздела, чтобы вычислить объем.
Источник
Рысси 2 года назад Какая формула? Приведите примеры, чтобы было понятно. Как найти объем жидкости в цилиндре, бочке в литрах? bezdelnik 2 года назад Полный объём ёмкости цилиндрической формы определяется по формуле V=S*H, где V -объём ёмкости в литрах, S – внутренняя площадь круглого основания ёмкости в квадратных дм, H -высота или длина цилиндра в дм. S=Пи*D^2/4, где Пи= 3,14… , D -внутренний диаметр цилиндра в дм. Поскольку Пи трансцендентное число то вычислить объём цилиндра можно только с некоторой погрешностью. Например, при D=10 дм и Н=10 дм V=Пи*100*10/4=Пи*1000/4= 3,14*250…=785… литров. Если полностью наполненную ёмкость наклонить, то чтобы найти объём Vо оставшейся в ней жидкости надо измерить расстояние h от верха ёмкости до оставшейся жидкости. Например, если в выше приведённой ёмкости расстояние h=H/2=5 дм, то Vо = V/2+V/4=3*V/4= 3*785/4= 588,75… литров. автор вопроса выбрал этот ответ лучшим комментировать в избранное ссылка отблагодарить Aitur Kabylbek 2 года назад Для измерения объема жидкости в емкости цилиндрической формы необходимо произвести расчеты по следующей формуле: Объем = Площадь (S) * Высоту (L). Площадь, в свою очередь, равна = число Пи * диаметр * диаметр / 4 = (3.14 * d^2) / 4. Теперь, нужно определить уровень жидкости в цилиндре. К примеру, мы положили туда тонкую палочку и определили высоту (L), до которой жидкость поднялась в цилиндре. Итоговая формула будет выглядеть следующим образом: V = ((3.14 * d^2) / 4) * L. в избранное ссылка отблагодарить Грустный Роджер A если это цилиндр, лежащий на боку? ТОгда формула совсем другая будет… il63 И тогда нужно задать длину цилиндра, его диаметр и высоту уровня воды от низшнй точки. Для ее решения без интегрирования можно обойтись? А если цилиндр лежит не горизонтально, а наклонен под углом альфа? Хорошая задача для вступительных экзаменов на физтех или в СПГУ. spin Если на боку, то тоже не так сложно. Надо только знать формулу площади сегмента окружности. И без всякого интегрирования задача решается. Знаете ответ? |
Источник
Объем определяет величину пространства, которую занимает какое-либо тело. Эта величина связана постоянными соотношениями с другими характеристиками физических тел – их геометрическими размерами, весом и плотностью. Поэтому измерение этих дополнительных параметров может стать базой для вычисления объема, например, сосуда.
Инструкция
Если есть возможность наполнить сосуд водой, то для определения его объема достаточно иметь какую-либо мерную форму. В зависимости от размеров сосуда мерной посудой может стать шприц, мензурка, стакан, банка, ведро или любая другая посуда, вместимость которой вам известна. Подобрав подходящий измерительный сосуд, заполните водой до краев сосуд исследуемый, а затем переливайте воду в измерительный сосуд, отсчитывая таким образом объем.
Если заполнить исследуемый сосуд жидкостью нет возможности, но можно поместить его в жидкость, то определите объем по количеству вытесненной им воды. Для этого тоже потребуется какая-либо мерная посуда. Заполнив ее частично водой, отметьте уровень, затем поместите в мерную посуду исследуемый сосуд таким образом, чтобы он полностью оказался под водой, и сделайте вторую отметку. Затем определите разницу объемов мерной посуды по разнице двух сделанных отметок.
Если мерной посуды нет, но есть возможность взвешивать сосуд, то определите разницу между сосудом пустым и заполненным водой. Исходя из того, что один кубический метр объема должен вмещать воду, весом в одну тонну, рассчитайте объем сосуда.
Если сосуд имеет геометрически правильную форму, то его объем можно рассчитать, измерив размеры. Для нахождения объема сосуда цилиндрической формы (например, кастрюли) надо измерить диаметр (d) его основания (дна кастрюли) и ее высоту (h). Объем (V) будет равен одной четверти от произведения возведенного в квадрат диаметра на высоту и число Пи: V=d²∗h∗π/4.
Для нахождения объема сосуда, имеющего форму шара, достаточно определить его диаметр (d). Объем (V) будет равен одной шестой части от произведения возведенного в куб диаметра на число Пи: V=d³∗π/6. Если измерить длину окружности (L) шарообразного сосуда в самой широкой его части проще (например, с помощью сантиметра), чем измерить диаметр, то объем можно рассчитать и через эту величину. Возведенную в куб длину окружности надо разделить на увеличенное в шесть раз число Пи, возведенное в квадрат: V=L³/(π²∗6).
Для нахождения объема (V) сосуда прямоугольной формы, надо измерить его длину, ширину и высоту (a, b и h) и перемножить полученные значения: V=a∗b∗h. Если этот сосуд имеет кубическую форму, то достаточно возвести длину одного его ребра в третью степень: V=a³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
Продолжая тему, начатую тут Объем жидкости в цилиндрической таре и в ответ на запрос Прошу помочь с расчётом публикуем калькулятор, вычисляющий объем жидкости в цилиндрической емкости под наклоном.
Для вычисления вам потребуется ввести параметры емкости (радиус и длину) замерить уровень жидкости вблизи от одного из оснований и угол наклона.
Замер уровня жидкости
Замер уровня жидкости должен производиться в диаметральной плоскости емкости перпендикулярно нижней цилиндрической стенке (см. рисунок), непосредственно у одного из оснований или на некотором расстоянии от него ( в этом случае надо заполнить параметр «Расстояние от основания при измерении»). Как вариант замера, в случае небольшого количества жидкости и если есть возможность наклонить емкость, можно наклонить ее таким образом, чтобы уровень у верхнего основания был нулевым. Тогда надо замерить только расстояние от верхнего основания до границы начала жидкости. Если же наклонить бочку так, что жидкость будет подходить ровно к верхнему углу (месту смыкания верхнего основания и боковой поверхности емкости) то уровень и расстояние до основания будут нулевыми, замерить потребуется только угол.
Детали и формулы расчета можно найти непосредственно под калькулятором.
Объем жидкости в наклонной цилиндрической таре
Расстояние от ближайшего основания при измерении уровня жидкости. (0 если измерение происходило непосредственно у основания).
Точность вычисления
Знаков после запятой: 2
Уровень жидкости у верхнего основания
Уровень жидкости у нижнего основания
Длина частично заполненной части
Длина полностью заполненной части
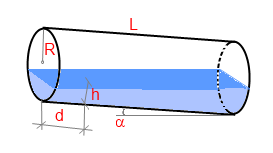Наклоненная цилиндрическая емкость
Готовой формулы для вычисления объема жидкости в наклонной емкости мне найти не удалось, поэтому пришлось ее выводить.
Если одно основание емкости заполнено полностью, то весь объем жидкости можно условно разделить на две части:
- цилиндрическая часть, объем которой находится тривиально по формуле объема цилиндра см. Цилиндр
- часть цилиндра усеченная под углом поверхностью воды. Объем этой части найти также не трудно по той же формуле, деленной пополам, если жидкость не доходит до верхнего основания (емкость стоит почти вертикально).
Формулы для вычисления объема частично заполненной части емкости
Сложности начинаются, если жидкость частично закрывает одно или оба основания, так как на рисунке.
Для вычисления объема такого тела мы заметим, что любое сечение этого тела перпендикулярно длине емкости представляет собой Сегмент круга. Тогда объем этого тела можно записать, как определенный интеграл по площади сегмента в зависимости от длины фигуры:
где -функция зависимости угла сегмента от длины фигуры x,
которая выражается следующим образом:
где
a — угол наклона емкости,
h0 — уровень жидкости у верхнего основания цилиндра (длина погруженной части верхнего основания) см. раздел Замер уровня жидкости
Подставим в формулу объема это выражение и упростив его получим полную формулу объема:
где
Вычислив интеграл, получаем:
где ,
Определение длины частично заполненной части
Приведенные выше формулы справедливы для следующих предположений:
- Оба основания заполнены частично
- Уровень жидкости h0 измерен непосредственно у верхнего основания с учетом наклона. (Фактически h0 – это длина погруженной части верхнего основания см. раздел Замер уровня жидкости).
- Нет полностью пустых или полностью заполненных частей цилиндра.
Но калькулятор может принимать на вход значения уровня жидкости, измеренные на некотором расстоянии от верхнего либо от нижнего основания. Допускаются полностью пустые и полностью полные части цилиндрической емкости.
Чтобы вычислить уровень жидкости у верхнего основания hu используйте формулы:
где hll – уровень жидкости, измеренный на расстоянии ll от нижнего основания, Lc – длина емкости
где hlu – уровень жидкости, измеренный на расстоянии lu от верхнего основания.
Если уровень huравен или больше нуля, мы считаем h0=hu, и Lf = Lc.
Пустая часть бака
В противном случае hu может быть отрицательным. Это означает, что какая-то часть бака пуста. В этом случае мы полагаем h0=0 и вычисляем длину оставшейся (заполненной) части цилиндра: Lf по формуле:
где Lc – длина цилиндра.
Полностью заполненная часть
Уровень жидкости у нижнего основания h1 можно определить следующим образом:
Если вычисленно значение h1 больше диаметра цилиндра, то некоторая часть цилиндра – заполнена полностью. Чтобы вычислить длину этой части мы используем формул:
Объем этой части посчитать тривиально: Цилиндр
После этих вычислений мы можем подставить длину частично заполненной части и уровень жидкости h0 в формулы первого раздела, чтобы вычислить объем.
Источник
В
заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о
погружении детали в жидкость или о переливании жидкости из одного сосуда
в другой.
Вопросы
в условии связаны с нахождением объёма погружаемого в жидкость тела или
с нахождением какого-либо параметра сосуда. Форма сосуда может быть
различной: цилиндр, призма.
Что необходимо понимать?
Если
жидкость залита в цилиндрический сосуд, то она принимает форму
цилиндра. Если она залита в имеющий форму призмы, то соответственно
принимает форму призмы. Это означает, что формулы для объёмов цилиндра и
призмы работают и для объёмов жидкостей помещённых в такие сосуды.
Формула объёма (цилиндра и призмы):
Если
жидкость перливается в аналогичный сосуд с меньшим основанием, уровень
(высота) жидкости увеличивается; если в сосуд с большим основанием, то
уровень жидкости уменьшается.
Рекомендации!
В
задачах на погружение детали в жидкость следует найти объём полученный
после её погружения, далее найти разность объёмов до и после (если
данные в условии это позволяют). Можно такие задачи решать и другим
способом, используя закон Архимеда. Примеры рассмотрены ниже.
В
задачах, где идёт речь о переливании жидкости в другой сосуд (с
уменьшенной или увеличенной площадью основания) помните о том, что сам
объём жидкости остаётся неизменным. Вы можете выразить его через площадь
основания и высоту (S1 и H1) одного сосуда и площадь основания и высоту (S2 и H2) другого сосуда, далее полученные выражения приравнять.
При
дальнейших преобразованиях получите отношение соответствующих величин –
либо площадей оснований, их рёбер, либо высот. Пример такой задачи
рассмотрен ниже в статье.
В цилиндрический сосуд налили 5000 см3
воды. Уровень жидкости оказался равным 40 см. В воду полностью
погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см.
Чему равен объем детали? Ответ выразите в см3.
Мы знаем, что объём цилиндра равна произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Высота это есть уровень жидкости.
Итак, из имеющихся данных можем найти площадь основания:
Основание
цилиндра у нас величина неизменная, но изменилась высота жидкости (при
погружении детали) на 15 сантиметров, то есть она стала
40 +15 = 55 см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 6875 – 5000 = 1875 см3
Можно решать подобные задачи более рациональным способом.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/45 исходного объема:
Ответ: 1875
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см3 воды
и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали?
Ответ выразите в см3.
Принцип решения тот же самый, что и в предыдущей задаче.
Мы знаем, что объём призмы равен произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Из имеющихся данных можем найти площадь основания призмы:
Основание призмы не изменилось, но изменилась высота жидкости (при погружении детали) она стала 24см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 3000 – 2500 = 500 см3
Второй способ:
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20 исходного объема:
Ответ: 500
Решить самостоятельно:
Посмотреть решение
В
сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 250 см. На какой высоте будет находиться уровень
воды, если ее перелить в другой такой же сосуд, у которого сторона
основания в 5 раз больше, чем у первого? Ответ выразите в см.
В
подобных задачах с переливаниями жидкости следует помнить, что объём её
остаётся прежним (он не изменен – куда бы её не перелили).
Объем
жидкости в данном случае это объём правильной треугольной призмы (в
её основании лежит правильный треугольник). Он равен произведению
площади основания призмы на высоту:
Суть
дальнейших действий сводится к тому, что мы можем выразить объёмы
жидкостей в двух призмах: первой и второй (основание которой в 4 раза
больше), а затем приравнять полученные выражения, в итоге после
преобразований получим отношение двух высот.
Естественно, что высота жидкости уменьшится, если увеличить площадь основания.
Обозначим исходную высоту жидкости Н1, полученную после переливания Н2.
Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:
Таким образом, объём залитой жидкости в первую призму равен:
Площадь основания второй призмы равна:
Объём залитой жидкости во вторую призму равен:
Найдём отношение высот:
Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.
Или можно сказать так:
При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.
Ответ: 10
Решить самостоятельно:
Посмотреть решение
В
цилиндрический сосуд, в котором находится 14 литров воды, опущена
деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему
равен объем детали? Ответ выразите в литрах.
Объём цилиндра равна произведению площади его основания на высоту:
Жидкость в сосуде имеет цилиндрическую объёмную форму.
Уровень
жидкости поднялся в 1,1 раза – означает, что высота цилиндра
увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что
при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также
в 1,1 раза (так как зависимость величин прямопропорциональная).
Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.
Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.
Ответ: 1,4
Решить самостоятельно:
Посмотреть решение
Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?
Например,
если дан начальный объём и высота жидкости (в сосуде формы призмы или
цилиндра), то мы можем найти площадь основания. Затем, зная площадь
основания и высоту жидкости после погружения детали мы можем найти
полученный объём.
Далее
найти разницу между объёмами не составит труда (это относится к первым
двум задачам). В последней задаче для решения требуется немного
логики.
Источник