Как вытекает вода из наполненного сосуда
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
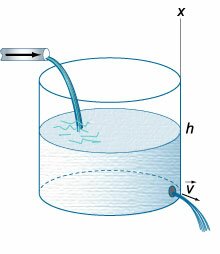
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
|
|
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
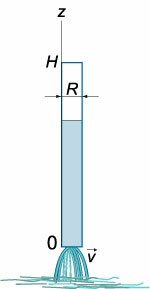
Вытекание жидкости из тонкой трубки
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
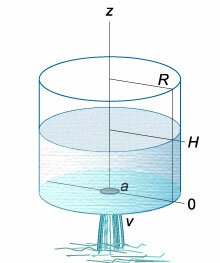
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
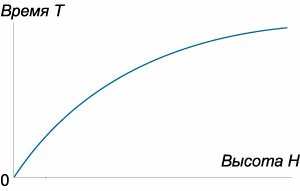
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
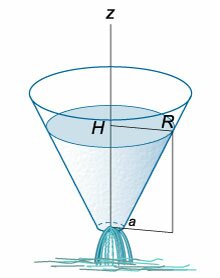
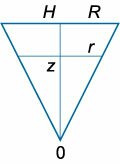
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
|
|
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
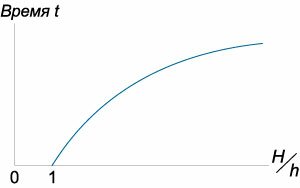
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Луиза Мальцева
24 июля · 757
Предположим, мы имеем сосуд в форме куба с параметрами 1м*1м*1м. При этом на дне данного сосуда есть пробоина, площадью S см^2. Сосуд равномерно заполняется жидкостью, плотность которой составляет ρ кг/м^3, со скоростью V килограмм в секунду. За какое время сосуд доверха заполнится жидкостью, если атмосферное давление равно p Па, а ускорение свободного падения – g? Также напишите, пожалуйста, какие для введенных переменных есть ограничения, чтобы выполнялось условие, что сосуд рано или поздно заполнится. Если данных недостаточно, введите, пожалуйста, свои обозначения для них. Заранее спасибо за ответ!
Автор вопроса считает этот ответ лучшим
Для скорости вытекания нужно воспользоваться формулой Торричелли.
где h – высота столба жидкости над отверстием
В килограммах в секунд эта скорость вытекания будет равна u = rho*S*v
Отсюда, кстати можно найти максимальную возможную высоту – когда скорость вытекания сравняется с V.
Теперь надо определить, за какое время наполнится до высоты h
Пусть S1 – площадь дна сосуда. Тогда скорость увеличения высоты благодаря втеканию V/(rho*S1) обозначим это константой a
А уменьшение благодаря вытеканию – S*sqrt(2*g*h)/S1. обозначим это все как b*sqrt(h)
Итого, складывая получим диффур
Он с разделяющимися переменными, поэтому легко интегрируется, и если я не наврал, то должно получится так t =
Правда в реальности формула Торричелли не совсем верна и не учитывает вязкость, и втекающий поток если очень сильный, будет создавать дополнительное давление, меняющее скорость.
Людовед, людолюб, “людоед”…
Количество жидкости прибывающей в сосуд должно быть больше, чем количество жидкости вытекающей из него в единицу времени (минута, час, сутки…) (назовем это “разница”). Надо соотнести объем сосуда. который нужно заполнить и разницу. И получим то время за которое сосуд заполниться. Если разница величина переменная, ведь с увеличением уровня воды… Читать далее
В каком сосуде на дно оказывается самое большое давление?
TL;DR в узком и высоком.
Чуть подробнее:
Давление (p) на дно сосуда расчитывается по формуле
p = ρgh, где
ρ – плотность жидкости
g – ускорение свободного падения
h – высота
Т.е. на давление напрямую не влияют:
– форма сосуда
– площадь и форма дна
– площадь и форма стенок
– и т.д.
Если же мы имеем фиксированный объем жидкости, и хотим налить её в такой сосуд, чтобы давление было максимальное, то нужно налить её в узкий и высокий сосуд, тогда высота столба жидкости будет максимальная и соответственно будет оказываться максимальное давление на дно.
Что будет, если вследствие неквалифицированного укола в вену в нее попадут пузырьки воздуха?
По образованию врач, по профессии — системный аналитик
Есть распространенный миф о том, что даже небольшой пузырек воздуха, случайно попавший в иглу, закупорит сосуд и вызовет мучительную смерть. На самом деле, маленькие пузырьки способны бесследно растворяться в крови, поэтому если вы не закачиваете воздух в вену целенаправленно, воздушной эмболии не произойдет.
Окружающий нас воздух на 78% состоит из азота. При нормальной температуре тела и нормальном атмосферном давлении (дело же происходит не высоко в горах?) на 100 мл крови может раствориться больше 1 мл азота и еще больше кислорода и углекислого газа. Случайный пузырек едва ли сможет приблизиться к такому большому объему. Тем не менее, специально вводить воздух в сосуд может быть опасно.
В плане воздушной эмболии гораздо опаснее, например, операции на открытом сердце и другие серьезные хирургические вмешательства, а также травмы.
Прочитать ещё 7 ответов
Источник
ВВЕДЕНИЕ.
Что такое вода?
Этот вопрос совсем не так неразумен, как это может показаться. В самом деле, разве вода — это только та бесцветная жидкость, что налита в стакан? Океан, покрывающий почти всю нашу планету, всю нашу чудесную Землю, в котором миллионы лет назад зародилась жизнь, — это вода. Тучи, облака, туманы, несущие влагу всему живому на земной поверхности, — это ведь тоже вода. Бескрайние ледяные пустыни полярных областей, снеговые покровы, застилающие почти половину планеты, — и это вода. Прекрасно, невоспроизводимо бесконечное многообразие красок солнечного заката, его золотых и багряных переливов; торжественны и нежны краски небосвода при восходе солнца. Этот великий художник природы — вода. Кроме того, разве все секреты воды открыты учеными? На этот вопрос сможет ответить только время. Почему нас заинтересовала вода?
Мы хотим узнать, может ли вода течь вверх?
Гипотеза: вода может течь вверх.
Цель исследования: исследовать, может ли вода течь вверх.
Задачи:
1. Изучить информацию о свойствах воды, используя научно–популярную литературу;
2. Провести физические опыты по исследованию свойств воды;
3. Выяснить, когда и при каких условиях вода поднимается вверх;
4. Сформулировать выводы.
При подготовке работы была изучена различная литература, изучены материалы Интернет–сайтов, применены знания, полученные на уроках окружающего мира и на кружке “Калейдоскоп наук”, проведен ряд опытов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Действие силы тяжести
Если вы выпустите книгу из рук, она неизбежно упадет на пол. “Виновата” в этом сила тяжести, которая притягивает все без исключения объекты к центру Земли. А подняв упавшую книгу, вы заметите, что ее внешний вид нисколько не изменился. Она – твердая, а твердые предметы сохраняют свою первоначальную форму. Если, конечно, не прикладывать к ним какую – либо специальную силу.
Теперь представьте себе, что упала не книга, а стакан с водой. Вода выплеснется и в беспорядке растечется. В самом деле, жидкость собственной формы не имеет. Она лишь занимает тот объем, ту форму, в которую налита. Все та же сила тяжести заставляет ее стремиться к самой низкой точке. Одним словом, где вода — там самое низкое место. Почему реки впадают в море? Просто уровень воды в морях ниже. Любая река как бы наклонена к тому морю, в которое она впадает. Ярким доказательством тому, что вода притягивается к Земле и стремится занять самый низкий уровень, являются водопады.
Сообщающиеся сосуды
Конечно, в обычном состоянии вода не сможет подниматься по склону, тем не менее, инженерам удалось заставить ее пересекать горные перевалы. Для этого оказалось достаточным… поместить воду в трубы. Именно так! Вода, бегущая в трубе со склона, давит на массы воды в трубе, поднимающейся в гору. И они, эти тысячи тонн воды, текут вверх! Правда, выше головы не прыгнешь: вода не поднимется выше своего первоначального уровня – высоты первой горы, с которой стекает. Но человек всегда найдет возможность сделать ту точку, из которой вытекает вода, самой высокой, и тогда никакие перевалы ему не страшны!
ЧЕГО НЕ ЗНАЛИ ДРЕВНИЕ?
Жители современного Рима до сих пор пользуются остатками водопровода, построенного еще древними: солидно возводили римские рабы водопроводные сооружения.
Не то приходится сказать о познаниях римских инженеров, руководивших этими работами; они явно недостаточно были знакомы с основами физики. Взгляните на прилагаемый рисунок, воспроизведенный с картины Германского музея в Мюнхене. Вы видите, что римский водопровод прокладывался не в земле, а над ней, на высоких каменных столбах. Для чего это делалось? Разве не проще было прокладывать в земле трубы, как делается теперь? Конечно, проще, но римские инженеры того времени имели весьма смутное представление о законах сообщающихся сосудов. Они опасались, что в водоемах, соединенных очень длинной трубой, вода не установится на одинаковом уровне. Если трубы проложены в земле, следуя уклонам почвы, то в некоторых участках вода должна течь вверх, — и вот римляне боялись, что вода вверх не потечет. Поэтому они обычно придавали водопроводным трубам равномерный уклон вниз на всем их пути (а для этого требовалось нередко либо вести воду в обход, либо возводить высокие арочные подпоры). Одна из римских труб, Аква Марциа, имеет в длину 100 км, между тем как прямое расстояние между ее концами вдвое меньше. Полсотни километров каменной кладки пришлось проложить из–за незнания элементарного закона физики!
ЧЕГО НЕ ЗНАЛИ МЫ?
Исследуя проблему воды, мы столкнулись с задачей. Перед нами было два кофейника одинаковой ширины: один высокий, другой — низкий. Какой из них вместительнее? В какой из этих кофейников можно налить больше жидкости?
Мы, не подумав, решили, что высокий кофейник вместительнее низкого. Однако когда стал лить жидкость в высокий кофейник, то налили его только до уровня отверстия его носика — дальше вода начала выливаться. А так как отверстия носика у обоих кофейников на одной высоте, то низкий кофейник оказался столь же вместительным, как и высокий с коротким носиком.
Это и понятно: в кофейнике и в трубке носика, как во всяких сообщающихся сосудах, жидкость должна стоять на одинаковом уровне, несмотря на то, что жидкость в носике весит гораздо меньше, чем в остальной части кофейника. Если же носик недостаточно высок, вы никак не нальете кофейник доверху: вода будет выливаться. Обычно носик устраивается даже выше краев кофейника, чтобы сосуд можно было немного наклонять, не выливая содержимого.
Капиллярные явления
При определенных обстоятельствах вода способна самопроизвольно подниматься вверх. Если поместить достаточно тонкую трубку (например, соломинку) в сосуд с водой, уровень воды в трубке поднимается выше уровня воды в сосуде. Разница между уровнями воды в сосуде и в трубке будет тем больше, чем меньше внутренний диаметр трубки. Способность воды подниматься в трубке с достаточно узким каналом – один из примеров, так называемых капиллярных явлений, благодаря которым растения способны доставлять воду из почвы к ветвям и листьям. Эти же явления помогают крови циркулировать в человеческом теле, особенно в капиллярах – мельчайших кровеносных и лимфатических сосудах. Кроме того, это происходит всегда и повсеместно. Сама поднимается вода вверх в почве, смачивая всю толщу земли от уровня грунтовых вод. Сама поднимается вода вверх по капиллярным сосудам дерева и помогает растению доставлять растворенные питательные вещества на большую высоту — от глубоко скрытых в земле корней к листьям и плодам. Сама движется вода вверх в порах промокательной бумаги, когда нам приходится высушивать кляксу, или в ткани полотенца, когда вытираем лицо.
Атмосферное давление
В старину – в 17–18 веках – вельможи забавлялись следующей поучительной игрушкой: изготовляли кувшин, в верхней части которой имелись крупные узорчатые вырезы. Такой кувшин, налитый вином, предлагали незнатному гостю, над которым можно было безнаказанно посмеяться. Как пить из нее? Наклонить нельзя: вино польется из множества отверстий, а до рта не достигнет ни капли. Случится, как в сказке:
Мед, пиво пил,
Да усы лишь обмочил.
–Как выпить содержимое?
Надо заткнуть отверстие В, взять в рот носик и втянуть в себя жидкость, не наклоняя сосуда. Вино поднимется через отверстие Е по каналу внутри ручки, далее по его продолжению С внутри верхнего края кувшина и достигнет носика.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Для выяснения того, как вода может течь вверх, мы провели ряд опытов.
Свои наблюдения мы занесли в таблицу:
Опыт 1 – с фонтаном
Для наблюдения используется опытный макет фонтана (два сообщающихся сосуда, соединенных резиновой трубкой). В один из сосудов (резервуар) наливается вода. Другой сосуд имеет отверстие, из которого “бьет фонтан”. Резервуар с водой опускается вниз и поднимается вверх. Вода в сообщающихся сосудах устанавливается на одинаковом уровне. Если резервуар поднимать, то вода сама поднимается вверх (из фонтана).
Опыт 2 – с цветком
Для опыта отбираются несколько цветков на стебле. В воде растворяется марганцево–кислый калий. Вода подкрашивается для того, чтобы можно было наблюдать за поднятием жидкости по стеблю. В подкрашенную воду опускаются цветы. Через некоторое время становится заметно, что подкрашенная вода сама поднимается вверх по стеблю. Ей помогает в этом атмосферное давление. При этом наблюдаются капиллярные явления. Через продолжительное время подкрашенная вода проникает даже в цветы.
Опыт 3 – с пробиркой
Для опыта используется: пробирка химическая, сосуд с горячей водой, сосуд с холодной подкрашенной водой.
Пробирка опускается в горячую воду так, чтобы открытый конец был вверху. Воздух в пробирке некоторое время прогревается. Затем открытый конец пробирки закрывается пластилином или большим пальцем. Пробирка очень быстро переворачивается и опускается в сосуд с холодной водой. Холодная вода сама начинает подниматься вверх. В этом воде помогает атмосферное давление.
В горячей воде воздух в пробирке прогревается, расширяется, частично выходит из пробирки. В холодной воде воздух сжимается. Атмосферное давление подталкивает воду в пробирку.
Опыт 4 – со шприцем
Для опыта используется: шприц демонстрационный или медицинский и сосуд с подкрашенной водой.
Вначале опыта поршень шприца до упора продвигается к отверстию шприца. После этого отверстие шприца опускается в подкрашенную воду. Поршень подтягивается вверх. Вода сама начинает подниматься вверх за поршнем.
В этом воде помогает атмосферное давление, которое подталкивает воду в разреженное пространство.
Опыт 5 – с сообщающимися сосудами
Для проведения опыта используются: электрическая плитка, теплоприемник, манометр, резиновая трубка, подкрашенная жидкость.
В сообщающиеся сосуды манометра наливается подкрашенная вода. Вода устанавливается на одинаковом уровне в обоих сосудах. Один из сообщающихся сосудов соединяется с теплоприемником резиновой трубкой. Разогретая электрическая плитка располагается напротив теплоприемника. Вода в одной из трубок сама начинает подниматься.
От разогретой плитки к теплоприемнику доходят тепловые лучи. Воздух в теплоприемнике нагревается, расширяется, давит на воздух над жидкостью в том сосуде, который соединен резиновой трубкой с теплоприемником. В этой трубочке вода начинает опускаться, а в другой трубке вода начинает подниматься.
Опыт 6 – с термометром
При проведении опыта сначала нужно рассмотреть шкалу термометра и определить температуру воздуха. Резервуар термометра удерживать некоторое время в ладони или опустить в горячую воду. Жидкость сама поднимается вверх по столбику. Резервуар термометра опустить в лед. Жидкость сама опускается.
При нагревании жидкость расширяется и поднимается по столбику. При охлаждении объем жидкости уменьшается, и жидкость опускается вниз.
ЗАКЛЮЧЕНИЕ
Все ли свойства воды понятны ученым!
Конечно, нет! Вода — загадочное вещество.
Недавно было обнаружено новое необыкновенное явление. Оказалось, что вода на Земле изменяет свою природу в зависимости от того, что происходит на Солнце и в космосе. Было замечено, что космические причины влияют на характер протекания в воде некоторых химических процессов, например на скорость появления осадков. Почему — неизвестно.
Многие наблюдения и факты говорят о том, что талая вода обладает особыми свойствами — она более благоприятна для развития живых организмов. Почему — тоже неизвестно.
Но для себя мы поняли, что:
– вода может двигаться вверх;
– вода может подниматься благодаря атмосферному давлению, например, в сообщающихся сосудах или капиллярах.
Можно не сомневаться, что все загадки будут успешно разрешены наукой. Будет открыто еще немало новых, более удивительных загадочных свойств воды — самого необыкновенного вещества в мире.
Литература
1. Всё обо всём. Популярная энциклопедия для детей.– М.: Слово, 1994.
2. Перельман Я. И. Занимательная физика. Книга 2.– М.: Наука, 1979.
Интернет–ресурсы
1. https://potomy.ru/things/149.html
2. https://www.aquaexpert.ru/enc/termin/water/
3. https://the-mostly.narod.ru/misc/fontain.html
4. https://brainmystery.ru/kogda-voda-techet-vverx/
5. https://www.origins.org.ua/page.php?id_story=263
6. https://class-fizika.narod.ru/p135.htm
Работу выполнили:
1. Камьянов Иван, 2–а класс
2. Митина Мария, 2–а класс
Руководители:
1. Беляевская Т.Я., учитель начальных классов
2. Дубас С.П., учитель физики
МОУ СОШ № 12 ЗАТО Шиханы Саратовской области
Источник