Какую часть объема сосуда должен занимать жидкий эфир
Переход вещества через критическое состояние характерен тем, что при этом исчезает различие между жидкой и газообразной фазами вещества. Критическое состояние характеризуется определенными для конкретного вещества параметрами: критическими температурой ($T_{kr})$, давлением ($p_{kr}$), объемом ($V_{kr}$). Если вещество, имеющее критическую температуру будет находиться в объеме не равном критическому, то состояние этого вещества критическим не будет. Различие между фазами в этом случае не исчезнет. Все вещество постепенно перейдет в одну фазу, при V${ > V}_{kr}$ вся жидкость испарится. При V${
Состояние реального газа
Рассмотрим реальный газ. Состояние такого газа опишем уравнением Ван-дер-Ваальса в виде:
Уравнение (1) является кубическим уравнением по отношению к объему, которое имеет переменные коэффициенты, зависящие от давления и температуры и свободный член. Такое уравнение может иметь Это уравнение имеет три корня. По отношению к решениям уравнения возможны следующие варианты в зависимости от соотношения коэффициентов: три вещественных корня, или один корень — вещественный, два комплексных. Так как объем может быть только вещественным, то комплексные решения смысла не имеют. Начиная с температуры, которая называется критической, при любом давлении, вещественным является только один корень уравнения. Критическая температура каждая своя для вещества.
Изотерма для газа Ван-дер-Ваальса
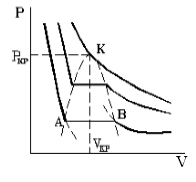
Опыт показывает, что изотерма для газа Ван-дер-Ваальса имеет вид рис.1, то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V(рис 1). Это область фазового перехода, где жидкость и газ существую одновременно.

Рис. 1
По мере увеличения температуры участок отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V) сужается, и превращается в точку (рис. 1). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.
Касательная к критической точке К параллельна оси V. Следовательно, производная $frac{dp}{dV}=0$ в точке К. Кроме того точка К является точкой перегиба, поэтому в ней равняется нулю и вторая производная: $frac{d^2p}{dV^2}=0$.
Пример 1
Задание: Найдите критические параметры газа описываемого уравнением Ван-дер-Ваальса.
Решение:
В качестве основания для решения задачи запишем уравнение Ван-дер-Ваальса (для одного моля газа, соответственно в уравнении V=$V_{mu }$):
[left(p+frac{a}{V^2}right)left(V-bright)=RTleft(1.1right).]
Выразим из уравнения (1.1) давление, получим:
[p=frac{RT}{V-b}-frac{a}{V^2} left(1.2right).]
Продифференцируем давление по объему ($frac{dp}{dV})$:
[frac{dp}{dV}=-frac{RT}{{left(V-bright)}^2}-frac{2a}{V^3} left(1.3right).]
Найдем вторую производную:
[frac{d^2p}{dV^2}=frac{2RT}{{left(V-bright)}^3}-frac{6a}{V^4} left(1.4right).]
В критической точке первая и вторая производные раны нулю. Запишем:
[frac{dp}{dV}=-frac{RT_{kr}}{{left(V_{kr}-bright)}^2}-frac{2a}{{V_{kr}}^3}=0 left(1.5right).]
[frac{d^2p}{dV^2}=frac{2RT_{kr}}{{left(V_{kr}-bright)}^3}-frac{6a}{{V_{kr}}^4}=0 left(1.6right).]
И из (1.2) для критического давления имеем:
[p_{kr}=frac{RT_{kr}}{V_{kr}-b}-frac{a}{{V_{kr}}^2} left(1.7right).]
Уравнения (1.5)-(1.7) образуют систему из трех уравнений с тремя неизвестными: $p_{kr}, T_{kr},V_{kr}.$ Решая эту систему, получим:
[V_{kr}=3b,]
[p_{kr}=frac{a}{27b^2},]
[T_{kr}=frac{8a}{27bR}.]
Так, зная постоянные Ван-дер-Ваальса a и b можно найти соответствующие критические параметры газа. И наоборот, по критическим параметрам газа можно вычислить константы уравнения Ван-дер-Ваальса.
Ответ: Критические параметры газа описываемого уравнением Ван-дер-Ваальса равны $V_{kr}=3b,p_{kr}=frac{a}{27b^2},T_{kr}=frac{8a}{27bR}.$
Пример 2
Задание: Какую часть объема сосуда должен занимать жидкий эфир при комнатной температуре, чтобы при достижении критической температуры он оказался в критическом состоянии? Для эфира $p_{kr}=35,5атм .,T_{kr}=467К, mu =74frac{г}{моль}, rho =714frac{кг}{м^3}$
Решение:
Для решения задачи используем результаты, полученные в предыдущем примере, а именно:
[V_{mu kr}=3b,p_{kr}=frac{a}{27b^2},T_{kr}=frac{8a}{27bR}(2.1)]
Найдем из (2.1) $frac{T_{kr}}{p_{kr}}$:
[frac{T_{kr}}{p_{kr}}=frac{8a}{27bR}frac{27b^2}{a}=frac{8b}{R}to b=frac{T_{kr}}{p_{kr}}frac{R}{8}left(2.2right)]
[V_{mu kr}=3b=frac{{3T}_{kr}}{p_{kr}}frac{R}{8}(2.3)]
Для того, чтобы наблюдался переход вещества через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем был равен критическому объему. Плотность жидкой фазы:
[rho =frac{m}{V_g}left(2.4right),]
где $V_g- $объем жидкости.
[frac{V_g}{V_{kr}}=frac{V_gmu }{mV_{mu kr}}=frac{mu }{rho V_{mu kr}} left(2.5right),]
где $V_{mu kr}$- критический молярный объем.
Используем (2.3) подставим $V_{mu kr}$- в (2.5), получим:
[frac{V_g}{V_{kr}}=frac{8mu }{rho R}frac{p_{kr}}{{3T}_{kr}}left(2.6right).]
Прежде чем провести вычисления, переведём данные в СИ:
[p_{kr}=35,5атм=35,5cdot {10}^5Па,T_{kr}=467К, mu =74frac{г}{моль}=74cdot {10}^{-3}frac{кг}{моль}]
Подставим данные в (2.6), получим:
[frac{V_g}{V_{kr}}=frac{8cdot 74cdot {10}^{-3}}{714cdot 8,31}frac{35,5cdot {10}^5}{3cdot 467}=0,25 left(2.7right)]
Ответ: 0,25 часть объема сосуда должен занимать жидкий эфир.
Источник

Заметим, что для идеального газа такое изменение внутренней энергии соответствовало бы нагреванию на 26,3К.
Ответ: ΔU=154 Дж.
67. В очень прочном стальном баллоне заключена вода, занимающая при комнатной температуре половину объема баллона. Найти давление (в технических атмосферах) и плотность водяных паров при повышении температуры до 400oС.
Решение. Из таблицы критических температур возьмем для воды t=374oС. Таким образом, при нагревании воды в баллоне до 400oС она оказалась при температуре выше критической. Следовательно, она вся будет находится в газообразном, или, как это принято говорить в отношении воды, парообразном состоянии.
Плотность водяного пара определим, учитывая, что объем одной и той же массы воды в результате ее нагревания увеличился в два раза (массу паров, находящихся над водой при комнатной температуре, можно не учитывать). Следовательно, плотность пара, равная отношению массы к объему, будет вдвое меньше плотности воды rВ=1×103 кг/м3:
r=rВ/2= 5×102 кг/м3.
Так как плотность пара в баллоне оказалась большой по сравнению с плотностями газов при нормальных условиях (например, плотность воздуха при нормальных условиях равна 1,29 кг/м3), то, очевидно, водяной пар здесь можно рассматривать как реальный газ, параметры которого связаны уравнением состояния Ван дер Ваальса:
.
Решив его относительно p, получим
Здесь Vo – молярный объем, но не объем всей массы пара. Поэтому на основании определения плотности можно записать
Vo=m/r, где m – молярная масса пара.
Подставив это значение Vo в вышенаписанную формулу, найдем
Взяв из таблиц значения постоянных a и b для воды, выразив все величины, входящие в формулу, в единицах СИ: Т=673 К, а=0,55 м4×Н/моль2, b=3×105 м3/моль, m=0,018 кг/моль. Выполнив вычисления, найдем
p=5,1×108 Па=5,2×103 ат.
Ответ: p=5,2×103 ат.
68. Определить давление m=280 г азота, находящегося при температуре 27 oС в сосуде, объем которого равен: 1) V=1,00 м3; 2) V=0,50 л.
Решение. Чтобы решить вопрос о том, каким следует считать данный газ – идеальным или реальным, найдем молярный объем газа Vo. Пусть в сосуде содержится n=m/m молей газа. Тогда
Vo=V/n=Vm/m.
Учитывая, что молярная масса азота m=0,028 кг/моль, получим:
1) Vo=1,00×0,28/0,28=0,10 м3/моль;
2) Vo=0,5×10-3×0,028/0,28=5,0×10-5 м3/моль.
Сравнивая вычисленные значения Vo с молярным объемом газа при нормальных условиях Vo(норм)=22,4×10-3 м3/моль, видим, что в первом случае газ достаточно разряжен и его можно считать идеальным. Уравнение состояния идеального газа для одного моля запишем так:
Отсюда
Во втором случае Vo<Vo(норм), и газ следует считать реальным. Его давление найдем из уравнения Ван дер Ваальса для реального газа
Взяв из таблиц значения постоянных Ван дер Ваальса для азота: a=0,13 м4×Н/моль2, b=3,7×10-5 м3/моль, произведем вычисление:
p=1,4×108 Па.
Заметим, что, вычисляя давление по формуле, характерной для состояния идеального газа, получили бы в этом случае неверный результат:
p=0,5×108 Па.
Ответ: p=0,5×108 Па.
69. Определить массу кислорода в баллоне объемом V=10,0 л при температуре 27 oС и давлениях:1)p1=1,00 ат; 2)p2=410 ат.
Решение. В первом случае (p=1,00 ат) кислород в баллоне находится при условиях, близких к нормальным. То обстоятельство, что температура газа несколько выше нормальной, означает лишь, что его плотность при этом давлении меньше, чем при нормальных условиях. Поэтому без большой погрешности можно считать газ идеальным. На основании уравнения состояния идеального газа, учитывая, что для кислорода m=0,032 кг/моль, получим:
кг.
Во втором случае (p=410 ат), учитывая большое по сравнению с нормальным давление газа, следует считать его реальным и вести расчеты на основании уравнения Ван дер Ваальса.
Масса газа определяется соотношением:
,
где m – молярная масса; n – число молей;
V – объем газа;
Vo – его молярный объем.
Таким образом, необходимо из уравнения Ван дер Ваальса
,
найти величину Vo, а затем массу газа.
Уравнение Ван дер Ваальса является уравнением третьей степени относительно V0 и поэтому имеет три корня.
Однако учитывая, что кислород в баллоне находится при температуре выше критической (tкр=-119 oС), можно утверждать, что при определенном давлении газ будет иметь лишь один определенный объем. Следовательно, кубическое относительно Vo уравнение Ван дер Ваальса имеет в данном случае лишь один действительный корень.
Его можно найти методом последовательных приближений, поскольку расчеты, связанные с решением кубического уравнения по общей формуле Кардано, весьма громоздки.
В качестве первого приближения вычислим молярный объем Vo1 газа, рассматривая его как идеальный. Тогда из уравнения состояния идеального газа получим
Теперь, обозначив в уравнении Ван дер Ваальса поправку на давление через po1=a/Vo2, найдем величину Vo
Взяв из таблиц значения постоянных a и b для кислорода, выразим в единицах СИ входящие в формулу величины: p=410×9,8×104 Па, Vo1=0,62×10-4 м3/моль, R=8,3 Дж/(моль×К), Т=300 К, a=0,13 м4Н/моль2, b=3,1×10-5 м3/моль. Выполнив вычисление, найдем
Vo2=0,65×10-4 м3/моль.
Еще раз, вычислив по формуле, полученной из уравнения Ван дер Ваальса, считая при этом p1=a/Vo22, получим третье приближение:
Vo3=0,66×10-4 м3/моль.
Повторяя таким образом вычисления, будем получать все более точные значения Vo:
Vo4=0,67×10-4 м3/моль;
Vo5=0,67×10-4 м3/моль.
Видим, что при дальнейших вычислениях, если ограничиться точностью до второго знака, результат не будет изменяться. Если же взять значение Vo5=0,68×10-4 м3/моль, то получим прежнее значение
Vo6=0,67×10-4 м3/моль.
Поэтому, действительным корнем кубического уравнения Ван дер Ваальса, вычисленным с точностью до второго знака, будет
Vo=0,67×10-4 м3/моль.
Теперь вычислим искомую массу газа
кг.
Легко убедиться в том, что вычисление по уравнению Менделеева-Клапейрона дало бы в этом случае неверный результат
кг.
Ответ: 1). m=0,013 кг; 2). m=4,8 кг.
70. Какую часть объема стеклянной ампулы должен занимать жидкий эфир при t=20 oС, чтобы при его нагревании можно было наблюдать переход вещества через критическое состояние? Для эфира m=0,074 кг/моль, r=714 кг/м3 при 20 oС, t=194 oС, p=35,6 ат.
Решение. Переход вещества через критическое состояние характерен тем, что при этом исчезает различие между жидкой и газообразной фазами вещества. Критическое состояние характеризуется определенными для каждого вещества параметрами: критическими значениями температуры Тк, давления pк и молярного объема V0к. При этом критический объем всей массы вещества, содержащей n=m/m молей, равен:
Vк=n V0к=(m/m) V0к.
Если вещество, нагретое до критической температуры Tк, окажется в объеме V, не равном Vк,то оно не будет при этом находиться в критическом состоянии. В этом случае при достижении температуры Tк не будет исчезать различие между двумя фазами, так как еще до достижения Tк все вещество при нагревании постепенно перейдет в одну фазу (при V>Vк вся жидкость в сосуде испарится, при V<Vк весь пар сконденсируется). Таким образом, для того чтобы наблюдать переход вещества, находящегося в ампуле, через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем V был равен критическому объему Vк.
Так как в этот момент вещество будет равномерно заполнять всю ампулу, то V является одновременно и объемом ампулы.
Искомое отношение объема Vж жидкого эфира к объему V ампулы найдем из ранее написанных уравнений, с учетом того, что m/Vж=r – плотность жидкого эфира:
Vж/V=Vж/Vк=mVж/mV0к=m/rVoк.
Выразив величину V0к через известные pк и Tк получим
Tк/pк=8a×27b2/27bRa=8b/R;
V0к=3b=3RTк/8pк.
Окончательно для искомого отношения имеем:
Vж/V=8mpк/(3RrTк).
Выразим в единицах СИ данные величины: m=0,074 кг/моль, p=35,6×9,8×104 Па, r=714 кг/м3, Тк=467 К. Подставив эти значения в формулу и выполнив вычисление, найдем
Vж/V=0,25.
Ответ: Vж/V=0,25.
71. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю теплоты, как и кирпичная стена толщиной d=40 см при одинаковой температуре внутри и снаружи здания? Коэффициенты теплопроводности кирпича и дерева равны соответственно: Кк=0,70 Вт/(м×К), Кд=0,175 ВТ/(м×К).
Решение. Количество теплоты, переданное через площадь S за время t, если расстояние между плоскостями d, а разность температур между ними DT, равно
Q=KDTtS/d,
где K – коэффициент теплопроводности.
Запишем уравнение теплопроводности через стену для обеих материалов:
Так как потеря теплоты должна быть одинаковое, т.е. Qк=Qд, имеем
.
Откуда толщина деревянной стены
dд=dкKд/Kк.
Подставим в полученное соотношение числовые значения в единицах СИ, после вычислений, будем иметь
dд=0,4×0,175/0,70=0,1 м.
Ответ: dд=0,1 м.
72. Стена нагревательной печи толщиной d=0,75 м выполнена целиком из огнеупорного шамотного кирпича с коэффициентом теплопроводности K1=1 Вт/(м×К). Какова будет толщина стены, если ее выполнить двухслойной, сохранив первый слой из того же материала толщиной d1=0,25 м, а второй слой из неогнеупорного, но малотеплопроводного, материала, у которого коэффициент теплопроводности K2=0,1 Вт/(м К)? Тепловой поток и температуры наружных поверхностей у двухслойной стены те же, что и у однослойной.
Решение. Тепловой поток – количество теплоты, переданное единичной площади в единицу времени, можно определить по формуле
где K – коэффициент теплопроводности;
DT – разность температур;
d – расстояние между двумя плоскостями.
Запишем уравнение теплового потока через однослойную стену и через каждый из слоев двухслойной:
q1=K1(t1-t3)/d,
q2=K1(t1-t2)/d1,
q3=K2(t2-t3)/d2.
Из каждого соотношения выразим изменение температур
(t1-t3)=qd/K1,
(t1–t2)=qd1/K1,
(t2-t3)=qd2/K2.
Складывая левые и правые части вышенаписанных формул, получим
2(t1-t3)=q(d/K1+d1/K1+d2/K2).
Подставим в последнее выражение значение q для однослойной стены и, преобразовав, имеем
d2=K2(d-d1)/K1.
Тогда общая толщина двухслойной стены будет равна:
d3=d1+d2=d1+K2(d-d1)/K1.
Подставив значения величин в единицах СИ, произведем вычисление
d3=0,3 м.
Ответ: d3=0,3 м.
73. Определить время подъема движущихся с постоянной скоростью пузырьков воздуха со дна водоема глубиной ℓ=1 м (рис. 3.15), если диаметры пузырьков соответственно равны 2 мм и 1 мм.
Решение. В рассматриваемом случае уравнение движения пузырьков имеет вид
ma=F+FA+Fс,
где m – масса пузырька;
a – его ускорение;
F=mg – сила тяжести;
FA – подъемная сила (сила Архимеда);
Fc – сила сопротивления (внутреннего трения).
Так как движение пузырька равномерное, то, очевидно, сила сопротивления движению уравновешивается подъемной силой; силой тяжести можно пренебречь, так как плотность воздуха во много раз меньше плотности воды. Предполагая, что пузырек имеет небольшой радиус и сферическую форму, то согласно закону Стокса, силу сопротивления движению можно определить по формуле:
Fс=6phr,
где h – коэффициент вязкости;
r – радиус пузырька;
v – его скорость.
Подъемая сила
FA=rogV=4pr3rog/3,
где ro – плотность воды;
g – ускорение силы тяжести.
Таким образом:
6phrv=4prrog/3,
или
6phrℓ/t=4prror3g/3,
где ℓ – путь, проходимый пузырьком;
t – время его движения.
Из последнего соотношения находим время движения пузырька
t=9hℓ/(2r2rog).
Подставив значения величин в единицах СИ, получим
t1=0,505 с; t2=2,02 с.
Ответ: t1=0,505 с; t2=2,02 с.
74. Чему равны при нормальных условиях коэффициенты диффузии и внутреннего трения азота, если эффективный диаметр молекулы азота d=3,1×10-10 м?
Решение. Из молекулярно кинетических представлений можно показать, что коэффициенты внутреннего трения и диффузии определяется соотношениями
;
,
где <v> – средняя арифметическая скорость молекул;
<λ> – их средняя длина свободного пробега;
ρ – плотность газа.
Средняя арифметическая скорость
,
где R – универсальная газовая постоянная;
Т – его абсолютная температура;
μ – молярная масса газа.
Средняя длина свободного пробега
,
где k – постоянная Больцмана;
d – эффективный диаметр молекулы;
p – давление газа.
Плотность газа можно определить воспользовавшись уравнением Менделеева-Клапейрона
.
Подставив величины, входящие в вышенаписанные формулы в единицах СИ <v>=457 м/с; <λ>=8,72×10-8 м, ρ=1,25 кг/м3, получим
η=16,6×10-6 кг/(м×с); D=1,36×10-5 м2/с.
Ответ: η=16,6×10-6 кг/(м×с); D=1,36×10-5 м2/с.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
©2015- 2021 zdamsam.ru Размещенные материалы защищены законодательством РФ.
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
