Какую часть объема сосуда в котором
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 — интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 — интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
2 октября 2011
Автор
КакПросто!
Объем определяет величину пространства, которую занимает какое-либо тело. Эта величина связана постоянными соотношениями с другими характеристиками физических тел – их геометрическими размерами, весом и плотностью. Поэтому измерение этих дополнительных параметров может стать базой для вычисления объема, например, сосуда.
Инструкция
Если есть возможность наполнить сосуд водой, то для определения его объема достаточно иметь какую-либо мерную форму. В зависимости от размеров сосуда мерной посудой может стать шприц, мензурка, стакан, банка, ведро или любая другая посуда, вместимость которой вам известна. Подобрав подходящий измерительный сосуд, заполните водой до краев сосуд исследуемый, а затем переливайте воду в измерительный сосуд, отсчитывая таким образом объем.
Если заполнить исследуемый сосуд жидкостью нет возможности, но можно поместить его в жидкость, то определите объем по количеству вытесненной им воды. Для этого тоже потребуется какая-либо мерная посуда. Заполнив ее частично водой, отметьте уровень, затем поместите в мерную посуду исследуемый сосуд таким образом, чтобы он полностью оказался под водой, и сделайте вторую отметку. Затем определите разницу объемов мерной посуды по разнице двух сделанных отметок.
Если мерной посуды нет, но есть возможность взвешивать сосуд, то определите разницу между сосудом пустым и заполненным водой. Исходя из того, что один кубический метр объема должен вмещать воду, весом в одну тонну, рассчитайте объем сосуда.
Если сосуд имеет геометрически правильную форму, то его объем можно рассчитать, измерив размеры. Для нахождения объема сосуда цилиндрической формы (например, кастрюли) надо измерить диаметр (d) его основания (дна кастрюли) и ее высоту (h). Объем (V) будет равен одной четверти от произведения возведенного в квадрат диаметра на высоту и число Пи: V=d²∗h∗π/4.
Для нахождения объема сосуда, имеющего форму шара, достаточно определить его диаметр (d). Объем (V) будет равен одной шестой части от произведения возведенного в куб диаметра на число Пи: V=d³∗π/6. Если измерить длину окружности (L) шарообразного сосуда в самой широкой его части проще (например, с помощью сантиметра), чем измерить диаметр, то объем можно рассчитать и через эту величину. Возведенную в куб длину окружности надо разделить на увеличенное в шесть раз число Пи, возведенное в квадрат: V=L³/(π²∗6).
Для нахождения объема (V) сосуда прямоугольной формы, надо измерить его длину, ширину и высоту (a, b и h) и перемножить полученные значения: V=a∗b∗h. Если этот сосуд имеет кубическую форму, то достаточно возвести длину одного его ребра в третью степень: V=a³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
Функциональные участки системы кровообращения. Объемы крови в различных отделах сосудистой системы
Как показано на рисунке, вся система кровообращения делится на системное кровообращение и легочное кровообращение. Поскольку системное кровообращение снабжает кровью все ткани организма, кроме легких, его называют также большим, или периферическим, кругом кровообращения.
Функциональные участки системы кровообращения. Прежде чем приступить к обсуждению функций системы кровообращения, очень важно понять функциональное значение отдельных ее участков.
Функцией артерий является подача крови к тканям под большим давлением. Поскольку кровь течет в артериях с большой скоростью, артерии имеют прочную сосудистую стенку.
Артериолы являются мелкими концевыми ветвями артериального русла и контролируют поступление крови в капилляры. Артериолы имеют сравнительно толстую гладкомышечную стенку, при сокращении которой просвет артериол может полностью закрываться. При расслаблении артериол их просвет увеличивается в несколько раз, что позволяет существенно увеличить объем крови, поступающей в сосудистое русло различных тканей в соответствии с их потребностями.
Функцией капилляров является осуществление обмена воды, питательных веществ, электролитов, гормонов и других веществ между кровью и тканевой жидкостью, поэтому стенка капилляров тонкая, имеет множество капиллярных пор, проницаемых для воды и других низкомолекулярных веществ.
Венулы собирают кровь из капилляров и, сливаясь, образуют более крупные венозные сосуды. По венам кровь направляется к сердцу. Вены — емкий резервуар, куда вмещается дополнительный объем крови. Стенка вен тонкая, поскольку давление в венозных сосудах очень низкое, однако в ней достаточно мышечных элементов, чтобы сокращаться или расслабляться. Итак, вены представляют собой контролируемую емкость, способную вмещать больший или меньший объем крови в зависимости от потребностей системы кровообращения.

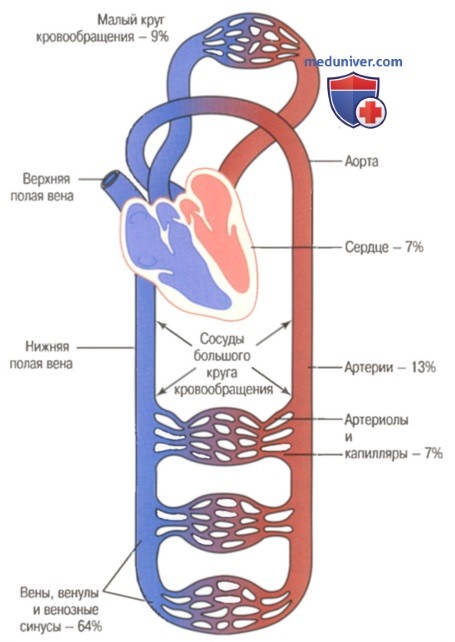
Распределение крови (% общего объема) в различных отделах сердечно-сосудистой системы
Объем крови в различных участках сосудистой системы. На рисунке представлена схема сердечно-сосудистой системы и указано, какая часть общего объема крови находится в том или ином участке системы кровообращения. Например, около 84% общего объема крови находится в большом круге кровообращения, а 16% — в сердце и легких. Из того объема крови, который находится в большом круге кровообращения, 64% находится в венах, 13% — в артериях и 7% — в артериолах и капиллярах. Сердце вмещает 7%, легкие — 9% общего объема крови.
Больше всего удивляет факт, что в капиллярах находится так мало крови. Ведь именно в капиллярах осуществляется наиболее важная функция сосудистой системы — диффузия и обмен веществ между кровью и тканями.
Площадь поперечного сечения и скорость кровотока. Если сосуды большого круга кровообращения расположить параллельно друг другу и определить суммарную площадь поперечного сечения сосудов каждого типа, то получим следующую картину:

Площадь поперечного сечения вен почти в 4 раза больше, чем площадь поперечного сечения соответствующих артерий, поэтому венозная система вмещает больший объем крови, чем артериальная система.
Скорость движения крови находится в обратной зависимости от суммарной площади поперечного сечения сосудов, поскольку один и тот же объем крови должен протекать через каждый участок сосудистой системы за минуту. Так, в состоянии покоя скорость движения крови в аорте в среднем равна 33 см/сек, тогда как в капиллярах она составляет всего 1/1000 скорости движения крови в аорте, т.е. около 0,3 мм/сек. Однако кровь находится в капилляре в течение 1-3 сек, поскольку длина капилляра только 0,3-1 мм. Удивительно, что за такое короткое время через стенку капилляра успевает произойти диффузия питательных веществ и электролитов.
– Также рекомендуем “Давление крови в различных участках сосудистой системы. Теоретические основы кровообращения”
Оглавление темы “Сосудистая система”:
1. Электрокардиограмма при фибрилляции желудочков. Электрошоковая дефибрилляция желудочков
2. Ручной массаж сердца в помощь дефибрилляции. Фибрилляция предсердий
3. Трепетание предсердий. Остановка сердца
4. Функциональные участки системы кровообращения. Объемы крови в различных отделах сосудистой системы
5. Давление крови в различных участках сосудистой системы. Теоретические основы кровообращения
6. Регуляция объема кровотока и периферического сопротивления. Объемный кровоток
7. Ультразвуковой флоуметр. Ламинарное течение крови в сосудах
8. Турбулентное течение крови. Давление крови
9. Сопротивляемость сосудов. Проводимость сосудов
10. Закон Пуазейля. Диаметр артериол и их сопротивление
Источник
