Капиллярную трубку опустили в сосуд с жидкостью
2017-10-13
Вертикальную капиллярную трубку с внутренним радиусом $r$ опускают нижним концом в жидкость с поверхностным натяжением $sigma$ и плотностью $rho$. Жидкость полностью смачивает поверхность капилляра. Какое количество теплоты выделится в процессе подъема жидкости?
Решение:
Почему вообще при подъеме жидкости в капилляре должно происходить выделение теплоты? Под выделением теплоты понимают необратимое превращение механической, электрической и других видов энергии в энергию хаотического теплового движения молекул. В этой фразе, по существу, уже содержится ответ на поставленный вопрос: начальное состояние системы, когда нижний конец капилляра пришел в соприкосновение с жидкостью,- это неравновесное состояние, из которого система самопроизвольно переходит в конечное равновесное состояние, причем этот переход совершается необратимым образом, с выделением теплоты.
Чтобы найти количество выделяющейся теплоты, рассмотрим детали этого необратимого процесса. В конечном состоянии столб жидкости покоится, поднявшись на высоту $h$, которую можно определить из условия механического равновесия. Действующая на столб жидкости сила тяжести $vec{P}$, равная по модулю $pi r^{2} h rho g$, уравновешивается действующей вертикально вверх силой $vec{F}$ поверхностного натяжения, приложенной к столбику жидкости по верхней кольцевой границе соприкосновения жидкости с внутренней поверхностью капилляра. Длина этой границы равна $2 pi r$, поэтому $F = 2 pi r sigma$. Приравнивая $P$ и $F$, находим
$h = 2 sigma / rho gr$. (1)
Центр масс этого столба массой $m = pi r^{2} h rho$ находится па высоте $h/2$ над поверхностью жидкости в сосуде. Поэтому его потенциальная энергия
$E_{п} – mgh /2 = 2 pi sigma^{2} / rho g$. (2)
Работа $A$ силы поверхностного натяжения, совершаемая при подъеме жидкости на высоту $h$, равна
$A = F cdot h = 4 pi sigma^{2} / rho g$. (3)
Видно, что эта работа силы поверхностного натяжения больше, чем потенциальная энергия столба жидкости. Очевидно, что избыток работы и равен искомому количеству выделившейся теплоты $Q$:
$Q = A – E_{п} = 2 pi sigma^{2} / rho g$. (4)
Интересно отметить, что при свободном подъеме, когда никакие другие силы, кроме сил тяжести и поверхностного натяжения, не действуют, количество выделившейся теплоты равно ровно половине работы силы поверхностного натяжения. При таком подъеме разогнанная силами поверхностного натяжения жидкость «проскакивает» по инерции положение равновесия. В отсутствие трения жидкость в капилляре совершала бы незатухающие колебания около среднего положения $h$, поднимаясь на максимальную высоту $2h$. Реально, даже при ничтожной вязкости жидкости, эти колебания постепенно затухают, что сопровождается выделением теплоты. При достаточно большой вязкости колебания вообще не возникают: на высоте h скорость жидкости уже уменьшается до нуля.
Количество выделяющейся теплоты можно сделать меньше и даже вообще сделать равным нулю, если обеспечить условия для обратимого перехода в конечное состояние. Для этого столбик жидкости в течение всего процесса подъема должен находиться в состоянии равновесия, т. е. кроме силы тяжести и силы поверхностного натяжения к нему нужно приложить еще дополнительную внешнюю силу. Обратимый переход в равновесное конечное состояние возможен только тогда, когда рассматриваемая система совершает работу над внешними телами. Кстати, подумайте, какую дополнительную внешнюю силу следует приложить к столбику жидкости в каждый момент его подъема, чтобы не происходило выделения теплоты? Какую работу совершит при этом система над внешними телами?
Даже получив ответы на эти вопросы, стоит еще задуматьея и над тем, за счет запаса какой энергии совершается работа силами поверхностного натяжения и как объяснить тот факт, что в конечном состоянии устойчивого равновесия потенциальная энергия оказывается больше, чем в исходном неравновесном состоянии. Дело в том, что наряду е потенциальной энергией в поле тяжести рассматриваемая система характеризуется еще и так называемой поверхностной энергией. Поверхностная энергия пропорциональна площади $S$ свободной поверхности жидкости:
$W_{пов} = sigma S$. (5)

рис.1
Это выражение можно получить, приравнивая работу, совершаемую внешними силами при увеличении площади поверхности горизонтальной пленки (рис. 1), приращению поверхностной энергии:
$F cdot x = 2 sigma lx = Delta W_{пов}$.
При перемещении перемычки на рис. 1 площадь свободной поверхности жидкости возрастает на $Delta S = 2lx$, так как пленка имеет две свободные поверхности. Поскольку рассматриваемое медленное изменение поверхности, при котором в каждый момент имеется равновесие сил, является обратимым, то поверхностную энергию можно считать потенциальной.
Если в системе может изменяться только поверхностная энергия, то состоянию устойчивого равновесия соответствует минимум площади свободной поверхности. Например, капли в свободном падении имеют сферическую форму, так как при заданном объеме шарообразная форма обеспечивает наименьшую поверхность.
По сути дела поверхностная энергия жидкости связана с различием в потенциальной энергии взаимодействия молекул жидкости, находящихся в объеме и в поверхностном слое. В расчете на одну молекулу эта энергия больше в поверхностном слое, чем в глубине жидкости. Поэтому увеличение свободной поверхности, когда часть молекул из объема переходит в поверхностный слой, требует совершения работы внешними силами.
Но при подъеме жидкости в капилляре ее свободная поверхность практически не изменяется. Значит, не изменяется и связанная со свободной поверхностью поверхностная энергия. Однако при подъеме в капилляре увеличивается поверхность соприкосновения жидкости со стеклом капиллярной трубки. Если жидкость смачивает поверхность твердого тела, т. е. самопроизвольно растекается по ней, то это значит, что энергия молекул жидкости в пограничном слое из-за взаимодействия с молекулами твердого тела меньше, чем энергия их внутри жидкости. Поэтому увеличение поверхности соприкосновения со стенками приводит к общему уменьшению потенциальной энергии взаимодействия молекул. В результате такое увеличение поверхности соприкосновения, в отличие от увеличения свободной поверхности, сопровождается совершением положительной работы силами поверхностного натяжения.
Итак, увеличение потенциальной энергии столба жидкости при его подъеме в капилляре, а также выделение теплоты происходят за счет уменьшения потенциальной энергии взаимодействия молекул при переходе их из глубины жидкости в граничащий со смачиваемой поверхностью слой.
Источник
Страница 3 из 5
7.41. Какую работу А против сил поверхностного натяжения надо совершить, чтобы разделить сферическую каплю ртути радиусом R = 3 мм на две одинаковые капли?
7.42. Какую работу А против сил поверхностного натяжения надо совершить, чтобы увеличить вдвое объем мыльного пузыря радиусом r = 1 см? Поверхностное натяжение мыльного раствора a = 0,043 Н/м.
7.43. Какую работу А против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь диаметром d = 4см? Поверхностное натяжение мыльного раствора
a = 0,043Н/м.
7.44. Найти давление p воздуха в воздушном пузырьке диаметром d = 0,01мм, находящемся на глубине h = 20 см под по-верхностью воды. Атмосферное давление p0=101,7 кПа.
7.45. Давление воздуха внутри мыльного пузыря на dр = 133,3 Па больше атмосферного. Найти диаметр d пузыря. Поверхностное натяжение мыльного раствора а = 0,043 Н/м.
7.46. На какой глубине h под водой находится пузырек воздуха если известно, что плотность воздуха в нем p = 2кг*м3?
Диаметр пузырька d = 15мкм, температура t = 20° С, атмосферное давление p0=101,3 кПа.
7.47. Во сколько раз плотность воздуха в пузырьке, нахо-.дящемся на глубине h = 5 м под водой, больше плотности воздуха при атмосферном давлении p0=101,3 кПа? Радиус пузырь-r = 0,5 мкм.
7.48. В сосуд с ртутью опущен открытый капилляр, внутренней диаметр которого d = 3 мм. Разность уровней в сосуде и в капилляре dh = 3,7 мм. Найти радиус R кривизны мениска в капилляре.
7.49. В сосуд с водой опущен открытый капилляр, внутренний диаметр которого d = 1мм. Разность уровней в сосуде и в капилляре dh = 2,8 см. Найти радиус кривизны R мениска в капилляре. Какова была бы разность уровней dh в сосуде и в капилляре, если бы смачивание было полным?
7.50. На какую высоту h поднимается бензол в капилляре, внутренний диаметр которого d = 1мм? Смачивание считать полным.
7.51. Каким должен быть внутренний диаметр d капилляру чтобы при полном смачивании вода в нем поднималась
dh = 2 см? Задачу решить, когда капилляр находится: а) на Земле, б) на Луне.
7.52. Найти разность уровней dh ртути в двух сообщавшихся капиллярах, внутренние диаметры которых равны d1=1мм и d2 =2 мм. Несмачивание считать полным.
7.53. Каким должен быть наибольший диаметр d пор в фиmиле керосинки, чтобы керосин поднимался от дна керосинки до горелки (высота h = 10 см)? Считать поры цилиндрическими трубками и смачивание полным.
7.54. Капилляр внутренним радиусом r = 2 мм опущен в жидкость. Найти поверхностное натяжение а жидкости, если известно, что в капилляр поднялась масса жидкости m = 0,09 г.
7.55. В сосуд с водой опущен капилляр, внутренний радиус которого r =0,16мм. Каким должно быть давление p воздуха
над жидкостью в капилляре, чтобы уровень воды в капилляре и с сосуде был одинаков? Атмосферное давление p0 = 101,3 кПа. Смачивание считать полным.
7.56. Капиллярная трубка опущена вертикально в сосуд с водой. Верхний конец трубки запаян. Для того чтобы уровень воды в трубке и в широком сосуде был одинаков, трубку пришлось погрузить в воду на 15% ее длины. Найти внутренней радиус r трубки. Атмосферное давление p0=100кПа. Смачивание считать полным.
7.57. Барометрическая трубка А, заполненная ртутью, имеет внутренний диаметр d, равный: а) 5мм; б) 1,5см. Можно ли определить атмосферное давление непосредственно по высоте ртутного столба? Найти высоту ртутного столба в каждом из этих случаев. Атмосферное давление p0= 758 мм рт. ст. Несмачивание считать полным.
7.58. Внутренний диаметр барометрической трубки d = 0,75 см. Какую поправку надо ввести, измеряя атмосферное давление по высоте ртутного столба? Несмачивание считать полным.
7.59. Какую относительную ошибку мы допускаем, вычисляя атмосферное давление p0= 101,ЗкПа по высоте ртутного столба.
если внутренний диаметр барометрической трубки d равен: а) 5мм; б) 10мм? Несмачивание считать полным.
7.60. На поверхность воды положили жирную (полностью несмачиваемую водой) стальную иголку. Каков наибольший диаметр d иголки, при котором она еще может держаться на воде?
Источник
Сегодня поверхностно рассматриваем тему поверхностного натяжения и решаем соответствующие задачи по физике.
Даже если вы не большой любитель жидкости, подписывайтесь на наш телеграм-канал, это интересно и полезно для всех.
Поверхностное натяжение, задачи
Задача №1. Поверхностное натяжение
Условие
Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия d=2 мм. Оказалось, что n=40 капель имеют массу m=1,9 г. Каким по этим данным получится коэффициент поверхностного натяжения «сигма»?
Решение
На каплю действует сила тяжести и сила поверхностного натяжения. Эти силы уравновешивают друг друга. Из условия задачи можно найти массу одной капли m0 и длину ее окружности l:
Далее запишем условие равновесия капли:
Отсюда находим коэффициент поверхностного натяжения:
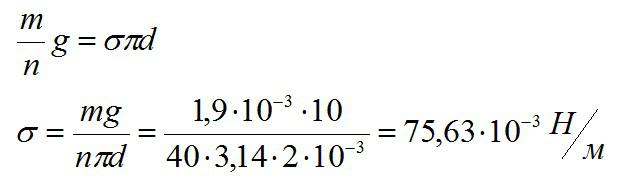
Ответ: 75,63*10^-3 Н/м.
Задача №2. Капиллярные явления
Условие
В капиллярной трубке радиусом 0,5 мм жидкость поднялась на высоту 11 мм. Оценить плотность данной жидкости, если ее коэффициент поверхностного натяжения равен 22 мН/м.
Решение
Для капилляра существует формула:
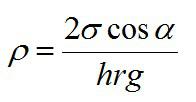
Альфа в этой формуле – угол смачивания стенки капилляра жидкостью. Пример его равным 90 градусов.
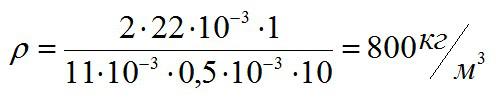
Ответ: 800 килограмм на кубический метр.
Задача №3. Поверхностное натяжение
Условие
В дне сосуда со ртутью имеется круглое отверстие диаметром 70 мкм. При какой максимальной высоте слоя ртути H она не будет вытекать через отверстие?
Решение
Ртуть не будет вытекать до тех пор, пока сила ее давления не превысит силу поверхностного натяжения:
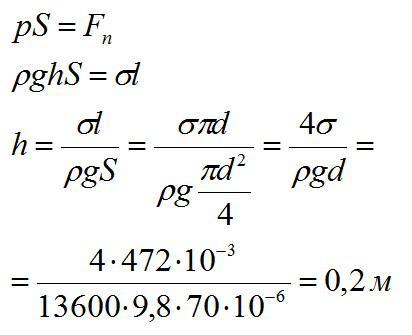
Значения коэффициента поверхностного натяжения разных жидкостей берутся в справочнике.
Ответ: 0,2 м.
Задача №4. Поверхностное натяжение
Условие
Швейная игла имеет длину 3,5 см и массу 0,3 г. Будет ли игла лежать на поверхности воды, если ее положить аккуратно?
Решение
Найдем силу тяжести, которая действует на иглу и сравним ее с силой поверхностного натяжения.
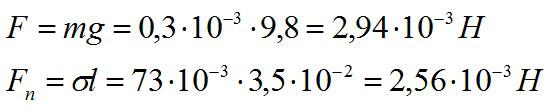
Ответ: Так как сила тяжести больше, игла утонет.
Задача №5. Поверхностное натяжение
Условие
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г.
Решение
На кольцо действуют силы поверхностного натяжения, сила тяжести и внешняя сила, стремящаяся оторвать кольцо от поверхности. Найдем силу поверхностного натяжения:
Множитель «2» используется в формуле, так как кольцо взаимодействует с жидкостью двумя своими сторонами.
Теперь запишем условие отрыва кольца:
Значение поверхностного натяжения мыльного раствора при комнатной температуре возьмем из таблицы, подставим числа, и получим:
Ответ: 0,11 Н.
Вопросы на тему «Поверхностное натяжение и свойства жидкостей»
Вопрос 1. Что такое жидкость?
Ответ. Жидкость – физическое тело, которое не может самостоятельно сохранять свою форму. Агрегатное состояние вещества между твердым телом и газом.
Вопрос 2. Какие свойства жидкости вы знаете?
Ответ. Среди основных свойств жидкости можно выделить:
- текучесть;
- вязкость;
- сохранение объема;
- поверхностное натяжение.
Вопрос 3. Что такое поверхностное натяжение?
Ответ. Поверхностное натяжение – это явление, при котором жидкость стремиться приобрести форму с наименьшей возможной площадью поверхности.
Примеры поверхностного натяжения в природе:
- Именно благодаря поверхностному натяжению в поле силы тяжести Земли жидкость приобретает форму капли.
- В отсутствие силы тяжести жидкости капля примет шарообразную форму.
- Водомерка удерживается на поверхности воды благодаря силе поверхностного натяжения.
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью S при постоянной температуре.
Вопрос 4. Что такое капиллярные явления?
Ответ. Капиллярные явления – подъем или опускание жидкости в капиллярах (трубках малого диаметра).
Вопрос 5. Что называется смачиванием?
Ответ. Смачивание – это искривление поверхности жидкости вблизи твердого тела. Возникает из-за взаимодействия молекул жидкости с молекулами твердого тела.
Количественная характеристика этого явления – угол смачивания.
Нужна помощь в решении заданий по учебе? Профессиональный студенческий сервис всегда готов ее оказать! Оформляйте заявку в любое время суток и забудьте о наболевших вопросах.
Источник
