Колебания жидкости в цилиндрическом сосуде
Рассмотрим подробнее вспомогательную краевую задачу для определения колебании жидкости в неподвижном сосуде и методы ее решения. Для некоторых простых полостей эта задача решается методом разделения переменных Фурье. В общем случае ее можно решить на ЭВМ интегральным методом Ритца или другими методами с использованием аналитических решений для простейших полостей [1].
В линейном приближении значительно упрощаются граничные условия для жидкости; их можно задавать на известной невозмущенной свободной поверхности жидкости и смоченной поверхности полости. Согласно (5), (6), (9), (11) и (14) функция должна быть гармонической в области занятой жидкостью в положении равновесия, и должна удовлетворять граничным условиям
где уравнение свободной поверхности жидкости в системе координат, жестко связанной с полостью так, что плоскость совпадает с невозмущенной свободной поверхностью жидкости (рис. 1).
Исключая из последних двух условий в (32) функцию получаем
После нахождения функции форма волны определяется выражением
Введем оператор Неймана
который ставит в соответствие функции функцию гармоническую в области и удовлетворяющую условиям если если Здесь функция Грина задачи Неймана для области
Рис. 1
Используя очевидное соотношение последнее условие в (32) представим в виде интегро-дифференциального уравнения для определения функции
Свободными (или собственными, или главными) колебаниями жидкости называют такие потенциальные течения, потенциал скоростей которых имеет вид
Число называют собственной частотой колебания.
На основании (34) форма поверхности волны свободного колебания определяется уравнением
Функция гармоническая в области и удовлетворяет граничным условиям
При подстановке (36) в (35) получим уравнение для определения функции
Таким образом, функции определяющие форму свободной поверхности жидкости, являются собственными функциями линейного оператора На основании общих теорем функционального анализа легко установить следующие свойства этих функций [13]:
1) при движении жидкости около положения равновесия в сосуде раниченных размеров существуют собственные колебания, т. е. решения вида
2) собственные числа положительные, имеют конечную кратность и образуют неограниченно возрастающую последовательность
3) собственные функции оператора которые описывают главные формы свободных колебаний жидкости, таковы, что последовательность функций полна и ортогональна;
4) собственные числа и собственные функции могут быть определены методом Ритца.
Для установления характера движения жидкости рассмотрим простейший пример плоских колебаний (в плоскости жидкости в канале прямоугольного сечения (рис. 2). Частные решения ищем в виде После разделения переменных в уравнении Лапласа и учета граничных условий (32) получим
где с — постоянная; любое натуральное число.
Таким образом, в прямоугольном канале могут возникать стоячие колебания жидкости, описываемые формулами (39). Таких форм колебаний бесчисленное множество, так как каждому натуральному числу соответствует своя форма колебаний. В каждом главном колебании при фиксированном у точка поверхности волны совершает периодические колебания с частотой В узлах при амплитуда равна нулю.
Рис. 2
Рис. 3
При фиксированном волна имеет форму косинусоиды. В моменты – свободная поверхность жидкости горизонтальна.
На рис. 2 изображена одноузловая форма главных колебаний, на рис. 3, а двухузловая и на рис. 3, б — трехузловая.
Обратим внимание на зависимость частоты от параметра (относительной глубины), которая приведена в таблице (через х обозначена величина
В работе [12], откуда заимствована эта таблица, приведены также таблица собственных частот, их зависимости от параметров для ряда других форм полостей и обширная библиография.
Величина собственной частоты заметно изменяется с глубиной только для очень мелких полостей и только для первых собственных частот, когда длина волны не очень мала. Для сосудов более или менее значительной глубины и для частоты с достаточной степенью точности справедлива приближенная формула Заметим, что для собственных частот колебаний жидкости в сосуде, глубина которого в 2 раза меньше ширины зеркала свободной поверхности, последняя формула дает погрешность не более 4%,
(см. скан)
Уравнения движения частиц жидкости, лежащих на определенной глубине, можно получить дифференцированием потенциала скоростей по
где
Частицы жидкости совершают прямолинейные колебания около своего начального положения с частотой и амплитудой Амплитуды убывают с глубиной по экспоненциальному закону и тем быстрее, чем больше частоты колебаний, На рис. 4 отрезками прямых изображены траектории частиц, лежащих на глубине Частицы жидкости, лежащие на одной вертикали с узлами, движутся по горизонтальным прямым.
Рис. 4
Главные колебания можно разделить на два типа: четные и нечетные. Для первого типа колебаний свободная поверхность представляет собой волну, симметричную относительно прямой Это волны четных индексов. Они не смещают центр тяжести жидкости в горизонтальном направлении. Можно показать, что никакими горизонтальными перемещениями сосуда нельзя вызвать на поверхности жидкости, которая в нем налита, волн этого типа. В свою очередь, подобные волны, возникшие вследствие каких-либо причин на поверхности жидкости, налитой в сосуд, не могут оказать никакого влияния на характер движения такого сосуда в горизонтальном направлении. Волиы нечетных индексов смещают центр тяжести с вертикальной прямой, и связанное с ними движение жидкости влияет на движение сосуда.
Источник
Содержание:
- Колебания жидкости в прямоугольном сосуде и в круговом цилиндре
Колебания жидкости в прямоугольном сосуде и в круговом цилиндре
Обратимся к случаю особого хода гидромеханики. Получаем следующие потенциальные потенциалы из формулы. Таким образом упростить уравнение. Выполняется в случаях. Во-вторых, может быть где-произвольное целое число.
Таким образом колебания тяжелой жидкости в сосуде , можно рассматривать движение жидкости, заключенной в прямоугольный контейнер любой ширины. Длина этого контейнера должна быть кратной. Давайте дадим прямоугольный контейнер длины и ширины. Затем, из условия Тебе решать.
- Предположим, вы хотите получить. Предположим, вы получите его соответственно. Уравнение дает соответствующую функцию, частоту и период.
- Если жидкость бесконечно глубокая, она выглядит так. И наоборот, если глубина жидкости мала по сравнению с длиной.
Уравнение показывает, что свободная поверхность является косинусом с полуволной.
Людмила Фирмаль
Показан узел вертикального перемещения, построенный для данного случая. Последнее определяется по формуле. В нашем случае это уравнение принимает вид.
Существуют следующие решения. Следовательно. Форма может колебаться узел. Так, в прямоугольных бассейнах разных эпох. Однако последнее определяется весьма специфическим образом. Это также верно и в других случаях.
- Чтобы получить более общий случай вибрации. Это сводится к тому, что ось будет не перпендикулярна к волновым панелям, а прямая линия, которая будет составлять ось и угол.
- Симметричное относительно оси движение определяется функцией. Линейность основного уравнения позволяет сформировать следующие решения.
Это означает простоту. Уравнение оптимизации является легко интегрируется. Обратите внимание только на конкретные решения ниже. Таким образом, можно возвести стену, на которой уравнение задается формулой, не нарушая движения жидкости.
Давайте дадим прямоугольный контейнер.
Людмила Фирмаль
Для простоты жидкость бесконечно глубока. Определяет частоту и длительность возможных флуктуаций в формуле (любое неотрицательное целое число). Если глубина жидкости мала. Указывается линия уровня поверхности корпуса.
Узловая линия — это линия, показанная на чертеже, параллельная осям. Чтобы проанализировать случай цилиндра, мы вместо этого вводим полярный. Основное уравнение принимает вид Самостоятельно найти решение этого уравнения. Вводим новую переменную для определения полученного уравнения Бесселя.
И так далее. Другими словами, если существует функция Бесселя нулевого порядка, проекция скорости в полярных координатах равна. Найти обтекаемость из уравнения. Таким образом, обтекаемость-это радиусы, расходящиеся от начала координат, а концентрические окружности-это корни уравнения. Дадим цилиндрический контейнер радиуса.
Затем из условия основные уравнения , которое вы определяете Уравнение имеет бесконечное число корней, первый из которых является сущностью. Поэтому она определяется из уравнения. Поэтому период колебаний становится для бесконечно глубоких жидкостей. Для неглубоких жидкостей. Узел вертикального перемещения определяется из уравнения. Так как первый корень уравнения равен
Источник
Метод Фурье разделения переменных применяют главным образом для цилиндрических полостей произвольного профиля с вертикальной образующей и плоским горизонтальным диом . В этом случае потенциал скоростей ищут в виде
Подставляя это выражение в исходные дифференциальные уравнения и граничные
условия, после разделения переменных получим следующие краевые задачи для функций и
где контур профиля цилиндрической полости; постоянная.
Задача (41) имеет нетривиальные решения лишь для определенных значений (собственных значений), при этом соответствующие собственные функции ортогональны на . Если контур совпадает с одной из координатных линий какой-либо криволинейной изотермической системы координат, то в (41) переменные х и у также разделяются и задача о свободных колебаниях сводится к решению обыкновенных дифференциальных уравнений. Решение задачи (40) имеет вид
если принять условие нормировки
Методом Фурье получены решения задачи о колебаниях жидкости в сосудах в форме параллелепипеда, кругового цилиндра, цилиндра с кольцевым дном, цилиндра с некоторым числом сплошных и несплошных перегородок и др. [11, 12].
Метод Ритца. Задача о свободных колебаниях жидкости в неподвижном сосуде может быть сведена к вариационной задаче для функционала [12, 13]
Для решения этой задачи используют метод Ритца, который в стандартном виде сводится к следующему: вводят полную ортонормированную систему «координатных» функций и решение задачи ищут в виде отрезка ряда с постоянными коэффициентами
где определяют из уравнений
Нетривиальные решения системы (44) существуют для значений X, удовлетворяющих уравнению частот
Так как матрицы симметричные, то корни уравнения (45) — действительные, при этом Решение уравнения (45) требует применения ЭВМ.
Основная трудность, с которой сталкиваются при практической реализации метода Ритца, состоит в выборе координатных функций. При этом следует иметь в виду следующее:
а) значение X, соответствующее низшей частоте, «мало чувствительно» к вы бору функций
б) можно не требовать, чтобы функции строго удовлетворяли всем граничным условиям; минимизирующая последовательность в этом случае также будет сходиться к точному решению.
Таким образом, систему координатных функций можно выбирать довольно грубо Достаточно только обеспечить полноту этой системы. В качестве функций целесообразно выбирать собственные функции задачи о колебании жидкости в некотором сосуде, охватывающем заданный, но имеющем более простую форму. Например, если жидкость колеблется внутри конического бака, то в качестве координатных функций можно взять собственные функции задачи о колебании жидкости в цилиндрическом сосуде, поперечное сечение которого равно наибольшему из оснований конуса.
Для оценки собственных частот колебаний жидкости используют следующее свойство если два сосуда имеют одинаковую площадь свободной поверхности и один сосуд объемлет другой, то соответствующие собственные частоты будут больше у того сосуда, объем которою больше [12].
Приближенный способ расчета собственных колебаний. Для определения собственных колебаний жидкости в области близкой к области для которой известна система собственных функций и собственных чисел X, целесообразно применять метод теории возмущений Этот метод позволяет для широкого класса полостей получить в явном виде приближенное решение с любой степенью точности.
Принимая в качестве координатных функций функции коэффициенты уравнений (44) представим в виде
Принимая условие нормировки получаем
Так как области малы, то формулы (46) можно преобразовать к виду
где символ Кронекера если если малый параметр.
Система уравнений (44) примет вид
Решение системы (47) разыскиваем в виде рядов
Для корня близкого к X, получим
Примеры, показывающие эффективность изложенного метода, приведены в монографии [12].
Определение потенциалов Стокса — Жуковского. Функции в формуле (26) можно определить теми же методами Фурье, Ритца и методом возмущений. При использовании метода Ритца минимизируют функционалы
Отыскание функции проводится с помощью метода Ритца в стандартном виде так, как показано в и. 5. Заметим, что в отчичие от задачи определения свободных колебаний здесь получится неоднородная система уравнений.
Источник
Задача о распространении волн в цилиндрической оболочке, заполненной или погруженной жидкость, имеет важное прикладное значение. Явление распространения волнообразного движения жидкости в упругих цилиндрических оболочках привлекало внимание исследователей [1, 2, 3, 4]. В этих работах, посвященных волновым процессам в системе упругой цилиндрической оболочки, рассматривается идеальная жидкость, используются классические и уточненные уравнения оболочек, рассмотрено влияние радиальных и продольных инерционных сил, учтена средняя плотность потока жидкости или газа. В работах [5, 6] проводится анализ закономерностей волнового процесса в упругой оболочке с вязкой жидкостью в рамках модели линеаризированных уравнений гидродинамики вязкой сжимаемой жидкости. В данной статье рассматриваются отличия систем цилиндрических оболочек (упругих или вязкоупругих) с жидкостью (идеальной или вязкой) от других, данная система рассматривается как диссипативно неоднородная механическая система [7, 8, 9].
Ключевые слова: цилиндрическая оболочка, жидкость, волновой процесс, диссипативно неоднородная, волнообразные движения
Постановка задача иметоды решения.
Рассматривается бесконечная по длине деформируемая (упругая или вязкоупругая) цилиндрическая оболочка радиуса R с постоянными толщиной , плотностью , модулем Юнга Е, — коэффициенты демпфирования в осевом и радиальном направлениях; коэффициентом Пуассона , заполненная вязкой жидкостью с плотностью в равновесном состоянии. Подлежат исследованию совместные колебания оболочки и жидкости, гармонические по осевой координате z и экспоненциально затухающие по времени, либо гармонические по времени и затухающие по z. Амплитуды колебаний считаются малыми, что позволяет записать основные соотношения в рамках линейной теории. Полную систему линеаризованных уравнений движения вязкой баротропной можно представить в виде [3]
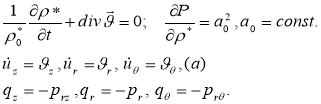
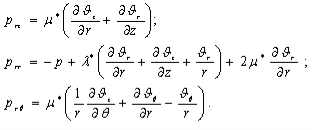 (1)
(1)
Здесь L – матрица дифференциальных операторов теории типа Крихгофа-Лява (или С. П. Тимошенко) [3]; – вектор перемещений точек срединой поверхности оболочки, причем для оболочек Кирхгофа-Лява он имеет размерность равную трем , а для оболочек типа Тимошенко размерность вектора равно пяти. Здесь кроме осевого, окружного и нормального перемещений добавляются еще углы поворота нормали к срединой поверхности в осевом и окружном направлениях; вектор усилия внешней нагрузки, приведенный к срединной поверхности оболочки. В уравнениях (1) = – вектор скорости частиц жидкости; и Р – возмущения плотности и давления в жидкости; и а – плотность и скорость звука в жидкости в состоянии покоя; — кинематический и динамический коэффициенты вязкости; для второго коэффициента вязкости принято соотношение =; – cоставляющие тензора напряжений в жидкости. Уравнений (1а) соответственно кинематические и динамические граничные условия, которые, в силу тонкостенности оболочки, будем удовлетворять на срединной поверхности (r=R). Соотношения (1) представляет замкнутую систему соотношений гидровязкоупругости для цилиндрической оболочки, содержащей вязкую сжимаемую жидкость. Так для оболочек, подчиняющихся гипотезе Кирхгофа-Лява, L – матрица дифференциальных операторов может записать:
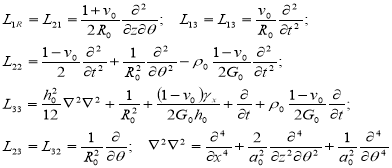 (2)
(2)
Компоненты вектора нагрузок для оболочек Кирхгофа-Лява имеют вид
(3)
где знак мине отвечает внутренней оболочке, а знак плюс-наружной — компоненты реакции со стороны жидкости (заполнителя); – интенсивность заданной нагрузки в соответствующем направлении. В осесимметричном случае на оси г=0 должны выполняться условия , =0. Если внешняя поверхность г=R предполагается неподвижной, тогда ur=uz=uφ=0. Раскрывая уравнения (1) в координатной форме, нетрудно заметить, что соотношения (1)-(3) распадаются на независимые краевые задачи:
– крутильные колебания:
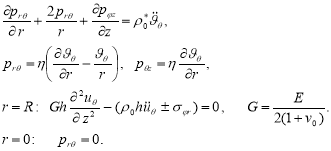 (4)
(4)
– продольно-поперечные колебания:
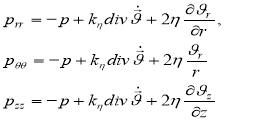 (5)
(5)
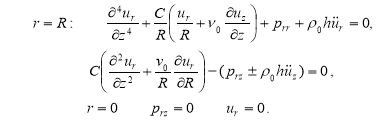
Пусть волновой процесс периодичен по z и затухает по времени, тогда задаётся действительное волновое число k, а комплексная частота является искомым собственным значением. Решения краевых задач (1)-(3) для основных неизвестных, удовлетворяющие наложенным выше ограничениям на зависимость по времени и координате z, следует искать в виде [3]
(6)
где вектор в правой части есть искомая комплекснозначная функция аргумента r, k, суть известного действительного и спектрального комплексного параметра от типа задачи. Суперпозиция решений (6) образует экспоненциально затухающую по времени стоячую волну, которая описывает собственные колебания жидкости и цилиндрической оболочки конечной длины с краевыми условиями. При бесконечной длине оболочки по аналогии указанный тип движения (6) будем называть собственными или свободными колебаниями. В случае стационарного по времени и затухающего по координате процесса, наоборот, известной является действительная частота , а искомым –комплексное волновое число k. В отличии от собственных, эти колебания условимся называть установившимися. Действительные части величин в первом случае, и k, во втором имеют физический смысл частот процесса по времени и координате соответственно. Мнимые части — скорость затухания волновых процессов по времени и Z соответственно [4]. Величину 1/Imk иногда определяют как интервал распространения затухающей волны. В предельном упругом случае интервал распространения бесконечен. Степень затухания волнового процесса на временном периоде характеризуется логарифмическим декрементом ,аналогично пространственный декремент равен
.
Можно ввести также понятия фазовых скоростей распространения собственных и установившихся движений
(7)
Продольно— поперечные колебания.
В этом параграфе проводится анализ стационарных продольно-поперечных колебаний оболочки, заполненной жидкостью, которые в соответствии с (5) могут быть описаны системой четырех обыкновенных дифференциальных уравнений
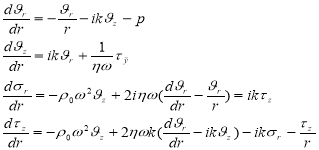 (8)
(8)
С краевыми условиями
(9)
Величина р в первом уравнении системы (8) определяется через основные неизвестные согласно выражению
(10)
Спектральная задача (8), (9), как и в случае продольно — поперечные колебания, решались методом ортогональной прогонки. Для нахождения корней характеристического уравнения использовался метод Мюллера.
Численные результаты.
Приведем результаты численного исследования собственных колебаний. На рис.1 показаны дисперсионные кривые зависимости от волнового числа k — для случаев несжимаемой (С0 = – штрихпунктирные линии) и сжимаемой (С0=0,1 — сплошные линии) жидкости. Параметры оболочки и коэффициенты вязкости приняты следующими:
h0 = 0,05; р=1,8; v0 = 0,25; h=6,011*10(-4); к=-2 η/3. Здесь и далее приводятся безразмерные величины, для которых единицы длины, времени и массовой плотности суть . Для несжимаемой жидкости существуют две моды, соответствующие преимущественно продольным (кривая 1) и преимущественно поперечным (кривая 2) колебаниям оболочки, с комплексными собственными значениями. Все остальные собственные движения имеют мнимые собственные значения, то есть апериодичны по времени. Пунктирными линиями на рис.1 обозначены дисперсионные кривые, соответствующие колебаниям оболочки с идеальной несжимаемой жидкостью. Решение последней задачи приводится ниже. Следует отметить, что в отличие от колебаний сухой оболочки совместные поперечные колебания оболочки жидкости для указанной плотности p1, происходит на меньшей по сравнению с продольными колебаниями частоте во всем диапазоне изменения волнового числа. При введении вязкости частота колебаний первой моды снижается, по-видимому, за счет вовлечения в движение дополнительных масс жидкости в пограничном слое, а у второй моды появляется критическое волновое число, ограничивающее область колебательных движений снизу. В работе [2], исследовавших установившиеся колебания, отмечалось стремление к нулю фазовой скорости низшей моды при уменьшении частоты. Собственные движения оболочки и вязкой сжимаемой жидкости имеют бесконечное число мод. В работе [3], использующего асимптотические методы решения, последний эффект обнаружить не удалось. На рис. 2 приводятся дисперсионные кривые для первых четырех мод с минимальными частотами колебаний (кривые 3,4,5,6) в порядке возрастания величины . Сравнивая кривые 1,2 и 3,4 между собой, можно убедиться, что вторая несколько хуже первой моды колебаний системы оболочка — сжимаемая жидкость для выбранных параметров удовлетворительно описываются моделью несжимаемой жидкости в области волновых чисел k 1. Это дает основание при исследовании указанной системы в первом приближении пренебречь сжимаемостью жидкости.
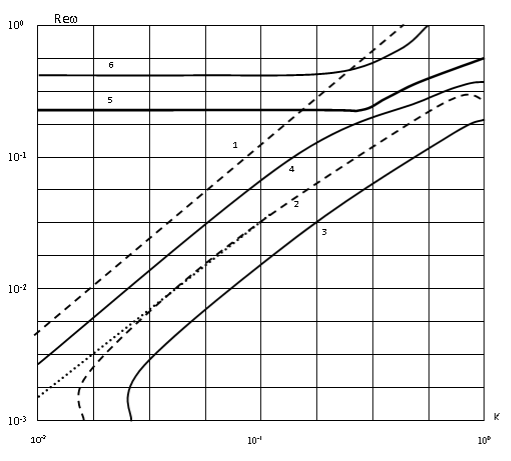
Рис. 1. Зависимость Re со от волнового число K (для случая несжимаемой жидкости)
Система упругая оболочка — вязкая жидкость является диссипативно-неоднородным вязкоупругим телом при радиальной координате. При этом в отличии от рассмотренных ранее крутильных колебаний здесь для несжимаемой жидкости имеются две, а для сжимаемой — неограниченное число колебательных мод. Представляет интерес выяснить, насколько в этой системе может проявиться синергический эффект. На рис.2 показаны дисперсионные кривые (1,2) для следующих параметров оболочки и жидкости:
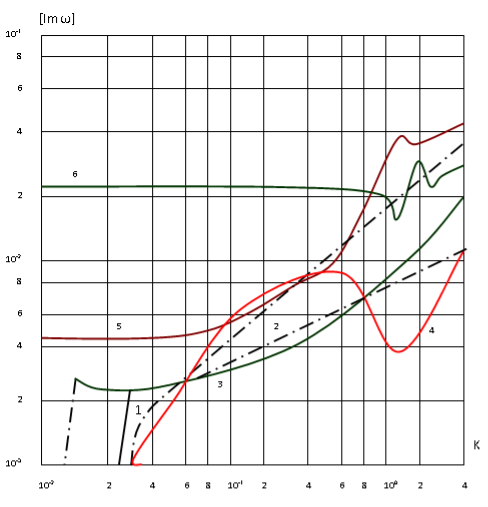
Рис. 2. Зависимость Im от волнового число K (для случая сжимаемой жидкости)
Штрихпунктирные линии соответствуют колебаниям сухой оболочки. Пунктирными линиями отмечены частотные зависимости для случая идеальной жидкости v = 0. В противоположность ранее рассмотренному варианту с плотностью р = 8, в данном случае парциальные частоты (v = 0) продольных и поперечных колебаний оболочки с идеальной жидкостью пересекаются между собой. Естественно ожидать, что при v вблизи точки пересечения парциальных частот будет иметь место сильная связанность обеих мод, приводящая к повышенной энергии, что выражается в синергическом эффекте. Действительно, о наличии мод свидетельствует эффект Вина – превращение продольной моды в поперечную, а поперечной в продольную при изменении волнового числа в окрестности пересечения парциальных частот. Нарушение монотонности роста и синергического эффекта. По сравнению с предыдущими описаниями этого эффекта здесь имеются две особенности. Во-первых, эффект проявляется вдали от места приближения кривых двух мод, во-вторых, кривые коэффициентов демпфирования не пересекаются между собой. В работе [6] исследовал связанность совместных колебаний идеального сжимаемого газа и оболочки с помощью диаграмм Вина. В качестве парциальных он рассмотрел частоты колебаний газа в жестких стенках и пустой оболочке. Возвращаясь к рис.2 отметим аналогичное проявление эффекта Вина в местах сближения кривых 4,5 и 5,6. В этих же местах на рис. 3 наблюдается для синергического эффекта кривых. Интересно проследить также влияние вязкости жидкости на связанность мод. Кривые 3,4 на рис.4 соответствуют значению коэффициента вязкости η=0,11 при неизменных остальных параметрах. В этом случае мода преимущественно поперечных колебаний определена на конечном интервале изменение волнового числа, а эффект Вина не наблюдается, что свидетельствует о слабой связанности мод. Еще большой рост вязкости (η=0,13, кривая 5) приводит к тому, что мода поперечных колебаний становится всюду апериодичной, а у продольных колебаний появляется критическое волновое число, ограничивающее область колебательных движений сверху. Физическая сущность обнаруженного эффекта раскрывается при анализе колебаний оболочки, заполненной идеальной жидкостью. Уравнения гармонических колебаний идеальной жидкости нетрудно вывести из соотношений (8), формально положив коэффициенты вязкости равными нулю.
(11)
общее решение системы (12), удовлетворяющее условию конечности неизвестных в нуле, имеет вид
(12)
где А произвольная постоянная:J0, Jl,- функции Бесселя нулевого и первого порядка соответственно для несжимаемой жидкости существует две действительные собственные функции Бесселя I0 и I1
(13)
В отличие от сухой оболочки здесь у второй частота запирания отсутствует, а фазовая скорость при малых k равна величине , которая совпадает со скоростью волны Резаля (см. обзор в начале главы). В случае сжимаемой жидкости и предельная фазовая скорость моды поперечных колебаний оболочки при k —> 0 есть скорость волны Кортевега- Жуковского . Численное исследование показало, что критическое значение Ck не зависит от вязкости жидкости, но с ростом величины η ослабевает зависимость колебаний коэффициента Пуассона, так что отношение а собственная форма U становится плоской. Как следует из приведенных результатов, в целом в рамках инженерной постановки задачи, нельзя адекватно описать продольные колебания цилиндрической оболочки, заполненной вязкой жидкостью с помощью стержневой теории.
Литература:
- Тер-Акопянц Г. Л. Об уточнении результатов влияния жидкости на распространение волн в упругой цилиндрической оболочке // Журнал. Фундаментальные исследования, технические науки № 10, 2013 г. С. 516–520.
- Сафаров И. И. Колебания и волны в диссипативно недородных средах и конструкциях. – Тошкент. Фан, 1992. – 250 с.
- Сафаров И. И., Тешаев М. Х., Болтаев З. И. Волновые процессы в механическом волноводе. LAP LAMBERT Academic publishing (Германия). 2012., 217 с.
- Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1996, 188 с.
- Каюмов С. С., Сафаров И. И. Распространение и дифракция волн в диссипативно — неоднородных цилиндрических деформируемых механических систем. Ташкент: ФАН, 2002 г, 214 с.
- Фролов К. В., Антонов А. Н. Колебания оболочек жидкости – М.: Наука, 1983. 365 с.
- Sorokin S. V. Fluid-Structure Interaction and Structural Acoustics. Book of Lecture Notes. — Technical University of Denmark, 1997. — 188 p.
- Вольмир А. С. Оболочки в потоке жидкости и газа: Задачи гидроупругости. — М.: Наука.1979. — 320 с.
- Гузь А. Н. Распространение волн в цилиндрической оболочке с вязкой сжимаемой жидкостью // Прикл. Механика. – 1980. – 16, № 10. – С. 10–20.
Основные термины (генерируются автоматически): цилиндрическая оболочка, волновой процесс, колебание, время, вязкая сжимаемая жидкость, жидкость, волновое число, вязкая жидкость, интервал распространения, несжимаемая жидкость.
Источник
