Количество молекул газа в сосуде

Задача 62. 
Вычислить массу: а) 2л Н2 при 15 °С и давлении 100,7кПа (755мм рт. ст.); 6) 1м3 N2 при 10 °С и давлении 102,9 кПа (772мм рт. ст.); в) 0,5 м3 Cl2 при 20 °С и давлении 99,9 кПа (749,3мм рт. ст.).
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где P  и V – давление и объём газа при температуре T; P0 (101,325кПа) и V0  – давление и объём газа при нормальных условиях; T0 (273К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газов при нормальных условиях:

Рассчитаем массу каждого газа, учитывая, что мольный объём газа равен 22,4л и, зная молекулярную массу газов, получим:

Ответ: а) 0,168г; б) 1.23кг; в) 1,456кг. 

Задача 63.
Определить объем, занимаемый 0,07кг N2 при 21°С и давлении 142 кПа (106 мм рт. ст.).
Решение:
Зная мольный объём и мольную массу азота (28г/моль), находим объём, который будет занимать 0,07кг (70г) азота при нормальных условиях:

Затем приведём полученный объём к температуре Т = 21оС (294К) и Р = 142кПа, используя выражение, объединяющее законы Гей-Люссака и Бойля-Мариотта:

где  P и V  – давление и объём газа при температуре  T; P0 (101,325кПа) и  V0 – давление и объём газа при нормальных условиях;  (273 К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газа при заданной температуре

Ответ: 43л.    

Задача 64. 
Бертолетова соль при нагревании разлагается с образованием КСI и О2. Сколько литров кислорода при 0 °С и давлении 101,3 кПа можно получить из 1 моля КСIО3?
Решение:
Уравнение реакции термического разложения бертолетовой соли имеет вид:

Из уравнения реакции следует, что из двух молей бертолетовой соли образуется три моля кислорода, т.е. из одного моля соли образуется полтора моля кислорода (2:3 = 1:х;   x = 1.3/2 = 1,5моль).

Объём кислорода при нормальных условиях (T0 =0 °С и P0 =101.325кПа) можно рассчитать по формуле: 

V(B) – объём газа, л;

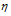(B)  – количество газа, моль;                               

 V(M) – мольный объём, 22,4л.

Тогда

 V(кислорода) = 1,5 . 22,4 = 33,6л.                      

Ответ: 33,6л.

Задача 65. 
Сколько молей содержится в 1м3 любого газа при нормальных условиях?
Решение:
Зная, что один моль любого газа при нормальных условиях (Т0 =0 °С и Р0 =101.325 кПа)  занимает 22,4л, рассчитаем количество молей газа в 1м3 (1000 л) из пропорции:

 Ответ: 44,64моль.

Задача 66. 
Чему равно атмосферное давление на вершине Казбека, если при 0 °С масса 1л взятого там воздуха равна 700 мг?
Решение:
Мольная масса воздуха равна 29 г/моль. Нормальными условиями для газов являются температура 0 °С и давление 101,325 кПа (760 мм рт ст.). Масса одного литра воздуха при нормальных условиях равна 1296,64 мг:

Теперь рассчитаем атмосферное давление на вершине Казбека из пропорции:

Ответ: 54,7к Па (410,3 мм рт. ст.).

Задача 67. 
При взаимодействии одного объема СО и одного объема Сl2 образуется один объем фосгена. Установить формулу фосгена.
Решение:
По условию задачи выходит, что из молекулы угарного газа и одной молекулы хлора образуется одна молекула фосгена. Так как молекула угарного газа СО состоит из одного атома углерода и одного атома кислорода, а молекула хлора Cl2 состоит из двух атомов хлора, то, следовательно, молекула фосгена будет состоять из одного атома углерода, одного атома кислорода и двух атомов хлора. Тогда формула фосгена будет иметь вид: CCl2O.
Уравнение реакции будет иметь вид:  

СО + Cl2 → ССl2O.           

Ответ: ССl2O. 

Задача 68. 
Какой объем СО2 получается при сгорании 2л бутана? Объемы обоих газов измерены при одинаковых условиях.
Решение:
Уравнение реакции горения бутана имеет вид:

  2С4Н10 + 13О2 = 8СО2 + 10Н2О                      

Из уравнения реакции следует, что при сгорании одного моля бутана образуется четыре моля углекислого газа. Известно, что при одинаковых условиях одинаковое количество газов занимают одинаковый объём. Один моль любого газа при нормальных условиях занимает объём в 22,4 л. 

Исходя, из этих утверждений рассчитаем объём выделившегося углекислого газа при сгорании 2 л бутана, составив пропорцию:

Ответ: 8л. 

Задача 69. 
В замкнутом сосуде при 120°С и давлении 600 кПа находится смесь, состоящая из трех объемов О2 и одного объема СН4. Каково будет давление в сосуде, если взорвать смесь и привести содержимое сосуда к первоначальной температуре?
Решение:
Уравнение реакции имеет вид:

CH4 + 2O2 →  CO2 + 2H2O                             

Из уравнения реакции следует, что из одной молекулы метана и двух молекул кислорода образуются одна молекула углекислого газа и две молекулы воды, т. е. реакция протекает без изменения объёма. Начальный объём системы состоял из одного объёма метана и трёх объёмов кислорода, после реакции в системе остался один объём не прореагировавшего кислорода и три объёма продуктов реакции (один объём метана и два объёма паров воды). Поскольку реакция протекает без изменения объёма, а по окончании реакции содержимое сосуда приводится к первоначальной температуре, а общее число молекул газов не изменилось, то давление в системе останется прежним, т. е. 600 кПа.

Ответ: не изменится.

Задача 70. После взрыва 0,020 л смеси водорода с кислородом осталось 0,0032 л кислорода. Выразить в процентах по объему первоначальный состав смеси. 
Решение:
Находим объём газов, вступивших в реакцию:

                         0,020 – 0,0032 = 0,0168 л.

Уравнение реакции горения водорода имеет вид:

2Н2 + О2 = 2Н2О                     

При взаимодействии водорода с кислородом из двух молекул водорода и одной молекулы кислорода получаются две молекулы воды, следовательно, из трёх молекул образовавшихся газов одна молекула будет принадлежать кислороду. Таким образом, объём кислорода, вступившего в реакцию, будет составлять одну треть объёма смеси газов – продуктов реакции. Отсюда количество кислорода, вступившего в реакцию, составляет 0,00565 л (0 0168/3 = 0,0056).

Следовательно, общее количество кислорода до реакции составляло 0,0088л (0,0056 +  0,0032 = 0,0088).

Тогда содержимое водорода до реакции составляло 0,0112л (0,02 – 0,0088 = 0.0112).

Рассчитаем в процентах первоначальный состав газовой смеси:

Ответ: 56%Н2; 44%О2.

Бесплатные решения задач из сборника А.Г. Чертова и А.А. Воробьева “Задачник по физике”.

9.1. В сосуде вместимостью V=12 л находится газ, число N молекул которого равно 1,44*1018. Определить концентрацию n молекул газа.

9.2. Определить вместимость V сосуда, в котором находится газ, если концентрация молекул n=1,25*1026 м-3, а общее их число N=2,5*1023…

9.3. В сосуде вместимостью V=20 л находится газ количеством вещества ν=1,5 кмоль. Определить концентрацию n молекул в сосуде.

9.4. Идеальный газ находится при нормальных условиях в закрытом сосуде. Определить концентрацию n молекул газа.

9.5. В сосуде вместимостью V=5 л находится кислород, концентрация n молекул которого равна 9,41*1023 м-3. Определить массу m газа.

9.6. В баллоне вместимостью V=5 л находится азот массой m=17,5 г. Определить концентрацию n молекул азота в баллоне.

9.7. Определить количество вещества ν водорода, заполняющего сосуд вместимостью V=3 л, если концентрация n молекул газа в сосуде равна 2*1018…

9.8. В двух одинаковых по вместимости сосудах находятся разные газы: в первом — водород, во втором — кислород. Найти отношение n1/n2 концентраций…

9.9. Газ массой m=58,5 г находится в сосуде вместимостью V=5 л. Концентрация n молекул газа равна 2,2*1026 м-3. Какой это газ?

9.10. В баллоне вместимостью V=2 л находится кислород массой m=1,17 г. Концентрация n молекул в сосуде равна 1,1*1025 м-3. Определить по…

9.11. В баллоне находится кислород при нормальных условиях. При нагревании до некоторой температуры часть молекул оказалась диссоциированной на атомы. Степень…

9.12. Определить концентрацию n молекул идеального газа при температуре T=300 К и давлении p=1 мПа.

9.13. Определить давление p идеального газа при двух значениях температуры газа: 1) T=3 К; 2) T=1 кК. Принять концентрацию n молекул газа равной ≈1019…

9.14. Сколько молекул газа содержится в баллоне вместимостью V=30 л при температуре T=300 К и давлении p=5 МПа?

9.15. Определить количество вещества ν и концентрацию n молекул газа, содержащегося в колбе вместимостью V=240 см3 при температуре T= 290 К и давлении…

9.16. В колбе вместимостью V=100 см3 содержится некоторый газ при температуре T=300 К. На сколько понизится давление p газа в колбе, если вследствие…

9.17. В колбе вместимостью V=240 см3 находится газ при температуре T=290 К и давлении p=50 кПа. Определить количество вещества ν газа и число N…

9.18. Давление p газа равно 1 мПа, концентрация n его молекул равна 1010 см-3. Определить: 1) температуру T газа; 2) среднюю кинетическую…

9.19. Определить среднюю кинетическую энергию <εп> поступательного движения и среднее значение <ε> полной кинетической…

9.20. Определить среднее значение <ε> полной кинетической энергии одной молекулы гелия, кислорода и водяного пара при температуре Т=400 К.

9.21. Определить кинетическую энергию <ε1>, приходящуюся в среднем на одну степень свободы молекулы азота, при температуре T=1 кК, а…

9.22. Определить число N молекул ртути, содержащихся в воздухе объемом V=1 м3 в помещении, зараженном ртутью, при температуре t=20 °С, если давление…

9.23. Для получения высокого вакуума в стеклянном сосуде необходимо прогревать его при откачке с целью удалить адсорбированные газы. Определить, на сколько повысится…

9.24. Определить температуру T водорода, при которой средняя кинетическая энергия <εп> поступательного движения молекул достаточна для…

9.25. Найти среднюю квадратичную <vкв>, среднюю арифметическую <v> и наиболее вероятную vв скорости молекул водорода. Вычисления…

9.26. При какой температуре T средняя квадратичная скорость атомов гелия станет равной второй космической скорости v2=11,2 км/с?

9.27. При какой температуре T молекулы кислорода имеют такую же среднюю квадратичную скорость <vкв>, как молекулы водорода при температуре T1=100…

9.28. Колба вместимостью V=4 л содержит некоторый газ массой m=0,6 г под давлением p=200 кПа. Определить среднюю квадратичную скорость <vкв>…

9.29. Смесь гелия и аргона находится при температуре T=1,2 кК. Определить среднюю квадратичную скорость <vкв> и среднюю кинетическую энергию…

9.30. Взвешенные в воздухе мельчайшие пылинки движутся так, как если бы они были очень крупными молекулами. Определить среднюю квадратичную скорость <vкв>…

9.31. Во сколько раз средняя квадратичная скорость <vкв> молекул кислорода больше средней квадратичной скорости пылинки массой m=10-8…

9.32. Определить среднюю арифметическую скорость <v> молекул газа, если их средняя квадратичная скорость <vкв>=1 км/с.

9.33. Определить наиболее вероятную скорость vв молекул водорода при температуре T=400 К.

Пример 1.
Определите число молекул, содержащихся в 2 мм³ воды при 4°С.

Дано

Решение

V = 2·10-9 м³

T = 277 К

______________

N = ?

Число молекул определим, используя выражение

,
(1)

где ν – количество вещества, NA–число
Авогадро.

Учитывая, что ν=m/μ, где μ-молярная масса,
использовав (1), получим:

. (2)

Массу воды определим через плотность и объем : m=ρV.
Тогда формула (2) примет вид:

. (3)

Молярную массу молекулы H2O воды вычислим:

(2·1+1·16)·10-3
кг/моль=18·10-3 кг/моль.

Окончательно, из формулы (3) получаем N≈6,68·1019
.

Пример 2. Поршневой насос, объем
цилиндра которого равен 0,5л, соединен с баллоном емкостью 3л, содержащим
воздух при нормальном атмосферном давлении. Определите давление воздуха в
баллоне после 5 рабочих ходов поршня, если насос работает в режиме: а) нагнетательном,
б) разрежающем. Считать процесс изотермическим.

Дано

Решение

V1=5·10-4 м³

V2=3·10-3 м³

p0=1,013·10-3 Па

n=5

______________

pн, pр –?

а) Поршневой насос после n-рабочих
ходов в нагнетательном режиме заберет из атмосферы объем воздуха Vn=nV1
при давлении p0. Этот воздух, попадая в баллон, создает там
парциальное давление pn. Тогда, согласно закону
Бойля-Мариотта (по условию Т=const),

, отсюда . Искомое
давление воздуха в баллоне:

б) По условию задачи воздух в баллоне занимает объем V2 при давлении р0. К концу первого
хода в разрежающем режиме та же масса воздуха займет объем V2+V1 при давлении p1.
Тогда по закону Бойля-Мариотта

, отсюда

В начале второго хода поршня объем и давление газа в баллоне
соответственно равны V2 и p1, а в конце хода – (V2+V1)
и p2, тогда

,

Следовательно, к концу n-го рабочего хода:

Подставляя числовые значения в выражения (1) и (2), получим

pн=1,86·105 Па; pр=0,48·105
Па.

Пример 3. Идеальный газ находится
под давлением 250 кПа и занимает объем 2,5л при температуре 200К. Сначала газ
изохорно нагревают до температуры 400К. Затем, изотермически расширяя, газ
доводят до первоначального давления. После этого газ возвращают в начальное
состояние путем изобарного сжатия. Изобразите процесс графически на
рV-диаграмме. Определите давление p2 и объем V3.

Дано

Решение

p1=2,5·103 Па

V1=2,5·10-3 м³

Т1=200К,

Т2=400К

______________

p2 – ? V3-?

Построим график цикла:

При переходе газа из состояния 1 в состояние 2 осуществляется
изохорный процесс. Следовательно, по закону Шарля имеем p1/Т1=p2/Т2,
откуда

(1)

При переходе газа из состояния 3 в состояние 1 осуществляется
изобарный процесс. Тогда, согласно закону Гей-Люссака , отсюда .

Учитывая, что Т3=Т2 (точки 2 и 3
принадлежат одной изотерме), получим

. (2)

Произведем вычисления по формулам (1) и (2): p2=5·105
Па; V3= 5·10-3 м³.

Пример 4. Идеальный газ находится в
баллоне при 27°С и давлении 3·106 Па. Какой станет температура,
если из баллона будет выпущено 0,3 массы газа, а его давление понизится до
2·106 Па?

Дано

Решение

Т1=300К

p1=3·106 Па

p2=2·106 Па

k=0,3

____________________

Т2-?

Рассмотрим два состояния идеального газа. В первом состоянии
газ имеет массу m и характеризуется параметрами p1, V и T, во
втором состоянии он имеет массу и характеризуется параметрами p2,
V и Т2.

Параметры каждого из этих состояний связаны уравнением
Менделеева-Клапейрона:

,(1)

. (2)

Разделив почленно уравнение (1) на уравнение (2), имеем:

, откуда .

Произведем вычисления, получим Т2=286К

Пример 5. В закрытом сосуде объемом
2м³ находится 2г водорода и 32г кислорода при температуре 500К.
Определите: а) давление в сосуде, б) молярную массу смеси, в) плотность
смеси.

Дано

Решение

V= 2м³

Т= 500К

m1=0,002 кг

m2=0,032 кг

µ1=2·10-3кг/моль

µ2=32·10-3кг/моль

R=8,31Дж/моль·К

_______________

p-? µсм-? ρсм-?

Давление смеси определим по закону Дальтона

, (1)

где p1- давление водорода, p2-
давление кислорода.

Из уравнения Менделеева-Клапейрона:

, .(2)

С учетом (2) преобразуем выражение (1):

.(3)

Для определения молярной массы смеси используем (3) в виде

(4)

Обозначив через µсм молярную массу смеси,
запишем уравнение Менделеева-Клапейрона для смеси в виде

. (5)

Из выражений (4) и (5) получим

. (6)

Плотность смеси газов определим из:

, (7)

где m=m1+m2 – масса смеси газов. Объем смеси газов из(4):

.(8)

Решая совместно уравнения (7) и (8), получим:

.(9)

Произведем вычисления по формулам (3), (6) и (9):

р=4,2 кПа, µсм=17·10-3 кг/моль,
ρсм= 0,017кг/м³.

Пример 6. Чтобы не стать помехой
движению самолетов, олимпийский аэростат «Миша», наполненный гелием при p1=105Па
и температуре T0=300К, должен был подняться над Лужниками на высоту
h=1,5км, где плотность воздуха на 20% меньше, чем у поверхности Земли. Какова
масса M оболочки аэростата, если его объем V=500м3 (оболочку
считать герметичной и нерастяжимой).

Дано

Решение

V=500м3

p0=105Па

T0=300K

h=1.5×103м

mв=29×10-3кг/моль

mг=4×10-3кг/моль

_____________________

Mобл=?

Анализ

Предполагаем, что T =const, а V =const из условия. Условия
равновесия аэростатавыполняются на высоте h =1500м. Тогда, из закона
Архимеда:

,

где mв – масса вытесненного воздуха, mг-масса
гелия.

Решив это уравнение, ответим на вопрос задачи

Выразим mв и mг mв=rвV, где rв = 0,8rвп,
где rвп – плотность
воздуха у поверхности земли.

Тогда

, а .

Следовательно

.

Аналогично .

Тогда

.

Произведем вычисление: M=380кг.

Пример 7. Спутник погрузился в тень
Земли. При этом температура внутри спутника, равная вначале T1=300K,
упала на 1%, вследствие чего давление воздуха изменилось на величину Dp=10,5×102Па.
Определите массу воздуха в спутнике, если его объем V=10м3.

Дано

Решение

T1=300K

DT=0.01

T=3K

Dp=10,5×102Па

V=10м3

m=29×10-3кг/моль

________________

m=?

Считаем, что газ (воздух) внутри спутника является идеальным.
Запишем уравнение Менделеева – Клайперона для каждого состояния:

,(1)

,(2)

(3)

Объем V, масса m, молярная масса m газа являются постоянными. В системе трех уравнений не
известны три величины: m, p1 и р2. Следовательно,
система разрешима.

Так как температура упала, то T1=T2+DT. Вычитая из уравнения (1) уравнение (2),
получаем

.

Но p1–p2=Dp, а T1–T2=DT. Тогда приходим к уравнению:

.

Отсюда: .

Произведем вычисления: m=12кг.

Пример 8. Идеальный газ, масса
которого равна 6,1кг, занимает объем 5м3 при давлении 2∙105Па.
Определите среднюю квадратичную скорость движения молекул газа.

Дано

Решение

m=6,1кг

V=5м3

р=2∙105Па

_____________

<кв>-?

Средняя квадратичная скорость молекулы: . Из уравнения
Менделеева – Клапейрона: найдем: . Тогда .

Произведя вычисления, получим: <кв> = 700м/с

Пример 9. В баллоне находится азот
массой 4г при 300К. Определите среднюю энергию поступательного движения
молекул, находящихся в баллоне.

Дано

Решение

m=4г= 4•10-3кг

Т=300К

μ = 28•10-3кг/моль

________________

<Wn> – ?

Средняя энергия поступательного движения всех молекул определяется
выражением:

; (1)

где <εn> – средняя энергия поступательного
движения одной молекулы; N – число молекул, находящихся в баллоне. Известно,
что ,(2)

где k=1,38•10-23Дж/К – постоянная Больцмана, Т
– термодинамическая температура. Число N молекул найдем по формуле:

, (3)

где n- количество
вещества, NА =6,02•1023моль-1 – постоянная
Авогадро.

Известно, что

,(4)

где m – масса азота, μ = 28•10-3кг/моль –
молярная масса азота.

Выражение (1) с учетом (2), (3) и (4) примет вид:

. (5)

Произведем вычисления по формуле (5), получим:
<Wn>≈534 Дж.

Пример 10. Смесь водорода и гелия
при температуре 27˚C находится под давлением 2∙102Па.
Масса водорода составляет 60% от общей массы смеси. Определите концентрацию
молекул каждого газа.

Дано

Решение

Т=300К

р=2•102Па

k=1,38•10-23Дж/К

τ1=0,6

τ2=0,4

_______________

n1, n2 – ?

Масса каждого из газов определяется из соотношений

, , (1)

где m – масса смеси, τ1 и τ2
– массовые доли соответственно водорода и гелия.

С другой стороны, масса каждого из газов:

, .
(2)

Сравнив (1) и (2), получим:

,

, откуда

. (3)

Для смеси газов

. (4)

Из выражения (3) и (4) получим:

,. (5)

При заданном давлении водород и гелий можно считать идеальными
газами, подчиняющимися уравнению , отсюда (6). С учетом
(6) преобразуем соотношения (5):

, . (7)

Произведем вычисления: n1 ≈ 0,36•1023,
n2 ≈ 0,12•1023.

Пример 11. Определите полную энергию
и количество молекул воздуха между рамами окна, если площадь окна S=2м2,
расстояние между рамами ℓ=0,2м. Давление воздуха между рамами
атмосферное, а температура его линейно изменяется вдоль ℓ от t1=
-10˚C (t1 – температура наружного стекла) до t2=20˚C
(t2–температура внутреннего стекла).

Дано

Решение

S=2м2

ℓ=0,2м

Т1=263K

Т2=293K

________________

W-?

N-?

По условию задачи, воздух между рамами находится в неравновесном
состоянии, так как температура изменяется вдоль оси Оx (Рис.2), ее
распределение в объеме воздуха не изменяется со временем. В пределах
достаточно тонкого слоя толщиной dx, температуру можно считать постоянной и
равной Т. Тогда энергия

.(1)

Концентрации молекул в пределах этого слоя определив из
уравнения состояния:

.(2)

Тогда число dN молекул в объеме слоя:

,(3)

а их энергия

.(4)

По условию задачи температура между рамами изменяется
линейно:

,
(5)

где α – постоянная.

Решая совместно уравнения (2), (3), (5), получим:

.

Тогда

(6)

Постоянные α и Т0 найдем из граничных условий: при
х=0 Т=Т1, следовательно, Т0=Т1; при
х=ℓ, Т= Т2, следовательно,

,

отсюда

.

Тогда

.(7)

Полная энергия dW всех молекул в слое dx:

.

Тогда

.(8)

Произведем вычисления по формулам (7) и (8), учитывая, что
i=5, р=1,01•105Па, N = 1,06•1025, W = 1•105Дж.

Пример 12. Определите среднюю
кинетическую энергию, среднюю энергию вращательного и среднюю энергию
поступательного движения одной молекулы аммиака NH3 при 27˚C.

Дано

Решение

Т=300К

________________

<ε>-?

<εn>-?

<εвр>-?

Средняя полная энергия молекулы:

,(1)

где i – число степеней свободы, k =1,38•10-23Дж/К
– постоянная Больцмана, Т – термодинамическая температура.

Средняя энергия поступательного движения молекулы:

, (2)

где число 3 означает число степеней поступательного движения
молекул. Средняя энергия поступательного движения молекул:

.

Учтя, что молекула аммиака является четырехатомной, т.е.
ее число степеней свободы равно 6, получим:

,

откуда

. (3)

Произведем вычисления по формулам (1) и (3):

<ε>=1,24•10-20Дж; =6,2•10-21Дж.

Пример 13. Определите среднюю
арифметическую скорость молекул идеального газа, плотность которого при
давлении 35кПа составляет 0,3кг/м3.

Дано

Решение

р=35×103Па

ρ=0,3кг/м3

_______________

<υ>-?

Согласно уравнению молекулярно – кинетической теории
идеальных газов

,(1)

где n – концентрация молекул, m0–масса одной
молекулы, <υкв> – средняя квадратичная скорость
молекул.

Учитывая, что , а , получаем:

.(2)

Так как плотность газа , где m – масса газа, V
– его объем, N – число всех молекул газа, то уравнение (1) можно записать в
виде:

или .

Подставляя это выражение в формулу (2), находим искомую
среднюю арифметическую скорость:

.

Вычисляя, получаем: <υ> = 545 м/с.

Пример 14. Используя функцию
распределения молекул идеального газа по относительным скоростям , где , определите число
молекул, скорости которых меньше 0,002 наиболее вероятной скорости, если в
объеме газа содержится N=1,67×1024
молекул.

Дано

Решение

υmax =0,002 υв

N=1,67×1024

_______________

DN-?

Число dN(u) молекул, относительные скорости которых заключены
в пределах от u до u+du

,(1)

где N – число молекул в объеме газа.

По условию задачи, υmax=0,002υв,
то umax= υmax/υв=0,002.

Так как u<1, то e-u² ≈ 1-u2. Пренебрегая
u2<1, выражение (1) можно записать в виде:

.(2)

Проинтегрировав выражение (2) по u в пределах от 0 до umax,
найдем

.

Вычисляя, получаем ∆N=1016 молекул.

Пример 15. Средняя длина
<ℓ> свободного пробега молекулы углекислого газа при нормальных
атмосферных условиях равна 40 нм. Определите среднюю арифметическую скорость
<υ> молекул и среднее число <z> соударений, которые испытывает
молекула в 1 секунду.

Дано

Решение

<ℓ> = 40×10-9м

_______________

<υ>-?, <z>-?

Средняя арифметическая скорость молекул определяется по
формуле:

,(1)

где μ- молярная масса вещества.

Среднее число соударений молекулы в 1 секунду равно отношению
средней скорости <υ> молекулы к средней длине <ℓ> ее
свободного пробега:

.(2)

Произведем вычисления по формулам (1) и (2):
<υ>=362м/с, <z>=9,05·109с-1.

Пример 16. Барометр в кабине
летящего самолета все время показывает одинаковое давление р=79кПа, благодаря
чему летчик считает высоту h1 полета неизменной. Однако температура
воздуха за бортом изменилась с t=5˚C до t=1˚C. Какую ошибку
∆h в определении высоты допустил летчик? Давление р0 у
поверхности Земли считать нормальным.

Дано