Количество теплоты полученное холодной водой из сосуда а равно

Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела – и котёл, и вода – будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С – 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2. Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3. Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4. В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5. На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

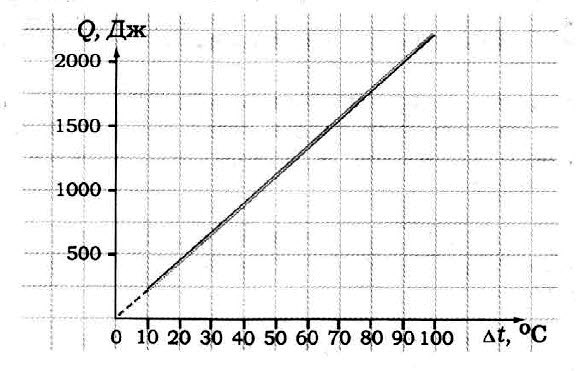
Задача № 6. По графику определите удельную теплоёмкость образца, если его масса 50 г.

Задача № 7. Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
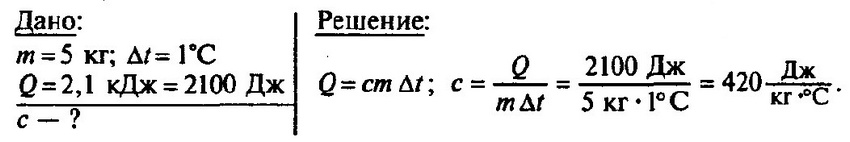
Задача № 9. Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10. Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11. а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12. ОГЭ Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13. В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности) Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник

Сравнение количеств теплоты при смешивании воды разной температуры.
Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене. Объяснить полученный результат.
Из учебника мы знаем, что при теплопередаче происходит переход энергии от одних тел к другим путем теплопроводности, излучения или конвекции. Энергия, которую получает или отдает тело при теплопередаче, называется количеством теплоты. Мы знаем также, что количество теплоты, необходимое для нагревания тела (или выделяемое им при остывании), зависит от рода вещества, из которого оно состоит, от массы этого тела и от изменения его температуры.
Итак, понятно, что в процессе теплопередачи между двумя телами их температуры стремятся уравняться. Тело с более высокой температурой отдает некоторое количество теплоты, а тело с более низкой температурой получает это количество теплоты. Причем в идеальных условиях, когда два этих тела абсолютно изолированы от всего на свете, переданное количество теплоты должно быть равно полученному согласно закону сохранения энергии.
Однако, условия проводимого нами эксперимента безусловно далеки от идеальных. От горячей воды тепло передается не только холодной воде, но и калориметру, термометру, окружающему воздуху. Тем не менее, хотя мы и не получим входе эксперимента полного соответствия отданного количества теплоты полученному, эти показатели, если эксперимент выполнен аккуратно, должны быть близки. Ход работы описан в учебнике.
Пример выполнения работы.

Вычисления:

Количество теплоты, отданное горячей водой – 12600Дж.
Количество теплоты, полученное холодной водой – 10920Дж.
Вывод: Количество теплоты, полученное холодной водой близко к количеству теплоты, отданному горячей водой, что, с учетом далеких от идеальных условий эксперимента, можно считать равенством.
Контрольные вопросы:
1) Как определялась в эксперименте масса воды?
Через плотность по формуле m=pV, т.е. косвенно, без использования весов. Так как плотность воды 1 г/см3, то масса 100 мл = 100 см3 будет 100г = 0,1 кг
2) Почему калориметр имеет двойные стенки?
Чтобы меньше терялась теплота в окружающую среду
3) Почему холодную воду надо брать комнатной температуры?
Чтобы её температура не изменялась из-за влияния воздуха в кабинете, т.к. она же не в калориметре
4) Будут ли равными изменения температуры и количество отданной и принятой теплоты, если использовать неравные массы теплой и холодной воды?
Изменения температуры не будут одинаковыми, а количество отданной и принятой теплоты будут равны
Суперзадание: объясните, как влияет на полученные результаты участие в теплообмене калориметра. Всегда ли можно этим влиянием пренебречь?
Ответ: Уравнение теплового баланса строго выполняется только в том случае, если система теплоизолирована. Хотя калориметр снижает потери энергии, связанные с теплопередачей в окружающую среду, тем не менее они остаются. Кроме того, есть потери за счёт теплообмена между водой и калориметром. Поэтому количество теплоты, одданное теплой водой, будет всегда больше, чем количество теплоты, полученное холодной водой. Если тёплую воду вливать в холодную, то различие между Qотд и Qпол будет больше, чем в случае, когда холодную воду добавляют в тёплую. Это обусловлено тем, что в первом случае потери энергии в окружающую среду будут частично скомпенсированы за счёт количества теплоты, которое холодной воде передают калориметр и термометр.
Таким образом, как это ни кажется странным, проверяемое положение о равенстве отданного и принятого количества теплоты выполнения работы будет подтверждено точнее, если в калориметр наливать сначала холодную воду, а затем доливать горячую (как и указано в работе).
Что касается второй части вопросы, всегда ли можно влиянием калориметра пренебречь? Нет, не в сегда. Можно пренебречь тогда, когда удельная теплоёмкость и масса внутреннего стакана калориметра мала по сравнению с массой воды (жидкости) находящейся в калориметре.
Источник

1. Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количеством теплоты.
Количеством теплоты называется изменение внутренней энергии тела в процессе теплопередачи без совершения работы.
Количество теплоты обозначают буквой ( Q ). Так как количество теплоты является мерой изменения внутренней энергии, то его единицей является джоуль (1 Дж).
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
2. Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество теплоты требуется ему для нагревания. То же самое и с охлаждением: тело большей массы при охлаждении отдаёт большее количество теплоты. Эти тела сделаны из одного и того же вещества и нагреваются они или охлаждаются на одно и то же число градусов.
[ Qsim m ]
3. Если теперь нагревать 100 г воды от 30 до 60 °С, т.е. на 30 °С, а затем до 100 °С, т.е. на 70 °С, то в первом случае на нагревание уйдёт меньше времени, чем во втором, и, соответственно, на нагревание воды на 30 °С, будет затрачено меньшее количество теплоты, чем на нагревание воды на 70 °С. Таким образом, количество теплоты прямо пропорционально разности конечной ( (t_2,^circ C) ) и начальной ( (t_1,^circ C) ) температур: ( Qsim(t_2-t_1) ).
4. Если теперь в один сосуд налить 100 г воды, а в другой такой же сосуд налить немного воды и положить в неё такое металлическое тело, чтобы его масса и масса воды составляли 100 г, и нагревать сосуды на одинаковых плитках, то можно заметить, что в сосуде, в котором находится только вода, температура будет ниже, чем в том, в котором находятся вода и металлическое тело. Следовательно, чтобы температура содержимого в обоих сосудах была одинаковой нужно воде передать большее количество теплоты, чем воде и металлическому телу. Таким образом, количество теплоты, необходимое для нагревания тела зависит от рода вещества, из которого это тело сделано.
5. Зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К), называется удельной теплоёмкостью вещества.
Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой ( c ). Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Удельная теплоёмкость свинца 140 Дж/кг °С. Это значит, что для нагревания 1 кг свинца на 1 °С необходимо затратить количество теплоты 140 Дж. Такое же количество теплоты выделится при остывании 1 кг воды на 1 °С.
Поскольку количество теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты ( Q ), необходимое для нагревания тела массой ( m ) от температуры ( (t_1,^circ C) ) до температуры ( (t_2,^circ C) ), равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
[ Q=cm(t_2{}^circ-t_1{}^circ) ]
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
6. Пример решения задачи. В стакан, содержащий 200 г воды при температуре 80 °С, налили 100 г воды при температуре 20 °С. После чего в сосуде установилась температура 60 °С. Какое количество теплоты получила холодная вода и отдала горячая вода?
При решении задачи необходимо выполнять следующую последовательность действий:
- записать кратко условие задачи;
- перевести значения величин в СИ;
- проанализировать задачу, установить, какие тела участвуют в теплообмене, какие тела отдают энергию, а какие получают;
- решить задачу в общем виде;
- выполнить вычисления;
- проанализировать полученный ответ.
1. Условие задачи.
Дано:
( m_1 ) = 200 г
( m_2 ) = 100 г
( t_1 ) = 80 °С
( t_2 ) = 20 °С
( t ) = 60 °С
______________
( Q_1 ) – ? ( Q_2 ) – ?
( c_1 ) = 4200 Дж/кг · °С
2. СИ: ( m_1 ) = 0,2 кг; ( m_2 ) = 0,1 кг.
3. Анализ задачи. В задаче описан процесс теплообмена между горячей и холодной водой. Горячая вода отдаёт количество теплоты ( Q_1 ) и охлаждается от температуры ( t_1 ) до температуры ( t ). Холодная вода получает количество теплоты ( Q_2 ) и нагревается от температуры ( t_2 ) до температуры ( t ).
4. Решение задачи в общем виде. Количество теплоты, отданное горячей водой, вычисляется по формуле: ( Q_1=c_1m_1(t_1-t) ).
Количество теплоты, полученное холодной водой, вычисляется по формуле: ( Q_2=c_2m_2(t-t_2) ).
5. Вычисления.
( Q_1 ) = 4200 Дж/кг · °С · 0,2 кг · 20 °С = 16800 Дж
( Q_2 ) = 4200 Дж/кг · °С · 0,1 кг · 40 °С = 16800 Дж
6. В ответе получено, что количество теплоты, отданное горячей водой, равно количеству теплоты, полученному холодной водой. При этом рассматривалась идеализированная ситуация и не учитывалось, что некоторое количество теплоты пошло на нагревание стакана, в котором находилась вода, и окружающего воздуха. В действительности же количество теплоты, отданное горячей водой, больше, чем количество теплоты, полученное холодной водой.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Удельная теплоёмкость серебра 250 Дж/(кг · °С). Что это означает?
1) при остывании 1 кг серебра на 250 °С выделяется количество теплоты 1 Дж
2) при остывании 250 кг серебра на 1 °С выделяется количество теплоты 1 Дж
3) при остывании 250 кг серебра на 1 °С поглощается количество теплоты 1 Дж
4) при остывании 1 кг серебра на 1 °С выделяется количество теплоты 250 Дж
2. Удельная теплоёмкость цинка 400 Дж/(кг · °С). Это означает, что
1) при нагревании 1 кг цинка на 400 °С его внутренняя энергия увеличивается на 1 Дж
2) при нагревании 400 кг цинка на 1 °С его внутренняя энергия увеличивается на 1 Дж
3) для нагревания 400 кг цинка на 1 °С его необходимо затратить 1 Дж энергии
4) при нагревании 1 кг цинка на 1 °С его внутренняя энергия увеличивается на 400 Дж
3. При передаче твёрдому телу массой ( m ) количества теплоты ( Q ) температура тела повысилась на ( Delta t^circ ). Какое из приведённых ниже выражений определяет удельную теплоёмкость вещества этого тела?
1) ( frac{mDelta t^circ}{Q} )
2) ( frac{Q}{mDelta t^circ} )
3) ( frac{Q}{Delta t^circ} )
4) ( QmDelta t^circ )
4. На рисунке приведён график зависимости количества теплоты, необходимого для нагревания двух тел (1 и 2) одинаковой массы, от температуры. Сравните значения удельной теплоёмкости (( c_1 ) и ( c_2 )) веществ, из которых сделаны эти тела.
1) ( c_1=c_2 )
2) ( c_1>c_2 )
3) ( c_1<c_2 )
4) ответ зависит от значения массы тел
5. На диаграмме представлены значения количества теплоты, переданного двум телам равной массы при изменении их температуры на одно и то же число градусов. Какое соотношение для удельных теплоёмкостей веществ, из которых изготовлены тела, является верным?
1) ( c_1=c_2 )
2) ( c_1=3c_2 )
3) ( c_2=3c_1 )
4) ( c_2=2c_1 )
6. На рисунке представлен график зависимости температуры твёрдого тела от отданного им количества теплоты. Масса тела 4 кг. Чему равна удельная теплоёмкость вещества этого тела?
1) 500 Дж/(кг · °С)
2) 250 Дж/(кг · °С)
3) 125 Дж/(кг · °С)
4) 100 Дж/(кг · °С)
7. При нагревании кристаллического вещества массой 100 г измеряли температуру вещества и количество теплоты, сообщённое веществу. Данные измерений представили в виде таблицы. Считая, что потерями энергии можно пренебречь, определите удельную теплоёмкость вещества в твёрдом состоянии.
1) 192 Дж/(кг · °С)
2) 240 Дж/(кг · °С)
3) 576 Дж/(кг · °С)
4) 480 Дж/(кг · °С)
8. Чтобы нагреть 192 г молибдена на 1 К, нужно передать ему количество теплоты 48 Дж. Чему равна удельная теплоёмкость этого вещества?
1) 250 Дж/(кг · К)
2) 24 Дж/(кг · К)
3) 4·10-3 Дж/(кг · К)
4) 0,92 Дж/(кг · К)
9. Какое количество теплоты необходимо для нагревания 100 г свинца от 27 до 47 °С?
1) 390 Дж
2) 26 кДж
3) 260 Дж
4) 390 кДж
10. На нагревание кирпича от 20 до 85 °С затрачено такое же количество теплоты, как для нагревания воды такой же массы на 13 °С. Удельная теплоёмкость кирпича равна
1) 840 Дж/(кг · К)
2) 21000 Дж/(кг · К)
3) 2100 Дж/(кг · К)
4) 1680 Дж/(кг · К)
11. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Количество теплоты, которое тело получает при повышении его температуры на некоторое число градусов, равно количеству теплоты, которое это тело отдаёт при понижении его температуры на такое же число градусов.
2) При охлаждении вещества его внутренняя энергия увеличивается.
3) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение кинетической энергии его молекул.
4) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение потенциальной энергии взаимодействия его молекул
5) Внутреннюю энергию тела можно изменить, только сообщив ему некоторое количество теплоты
12. В таблице представлены результаты измерений массы ( m ), изменения температуры ( Delta t ) и количества теплоты ( Q ), выделяющегося при охлаждении цилиндров, изготовленных из меди или алюминия.
Какие утверждения соответствуют результатам проведённого эксперимента? Из предложенного перечня выберите два правильных. Укажите их номера. На основании проведенных измерений можно утверждать, что количество теплоты, выделяющееся при охлаждении,
1) зависит от вещества, из которого изготовлен цилиндр.
2) не зависит от вещества, из которого изготовлен цилиндр.
3) увеличивается при увеличении массы цилиндра.
4) увеличивается при увеличении разности температур.
5) удельная теплоёмкость алюминия в 4 раза больше, чем удельная теплоёмкость олова.
Часть 2
C1.Твёрдое тело массой 2 кг помещают в печь мощностью 2 кВт и начинают нагревать. На рисунке изображена зависимость температуры ( t ) этого тела от времени нагревания ( tau ). Чему равна удельная теплоёмкость вещества?
1) 400 Дж/(кг · °С)
2) 200 Дж/(кг · °С)
3) 40 Дж/(кг · °С)
4) 20 Дж/(кг · °С)
Ответы
Количество теплоты. Удельная теплоёмкость
2.9 (58.29%) 35 votes
Источник
