Концентрация газа в сосуде

В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.
Идеальный газ
Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.
Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.
Универсальное уравнение
Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
P * V = n * R * T.
Где R – постоянная, равная 8,314 Дж/(моль*К), n – количество вещества.
Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).
Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций
Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.
В случае газов, как правило, пользуются тремя следующими концентрациями:
- Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
- Массовая. Показывает отношение массы компонента к объему газа.
- Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.
Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.
Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.
Формула концентрации молекул газа
В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:
cn(i) = ni / V.
Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:
P * V = n * R * T =>
cn = n / V = P / (R * T).
Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
cn = n / V = N / (NA * V) = cN / NA =>
cN = cn * NA = NA * P / (R * T) = P / (kB * T).
Здесь NA и kB – число Авогадро и постоянная Больцмана. Соответственно, N – число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10-23), то cN принимает огромные значения, что неудобно для ее практического использования.
Пример задачи
В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.
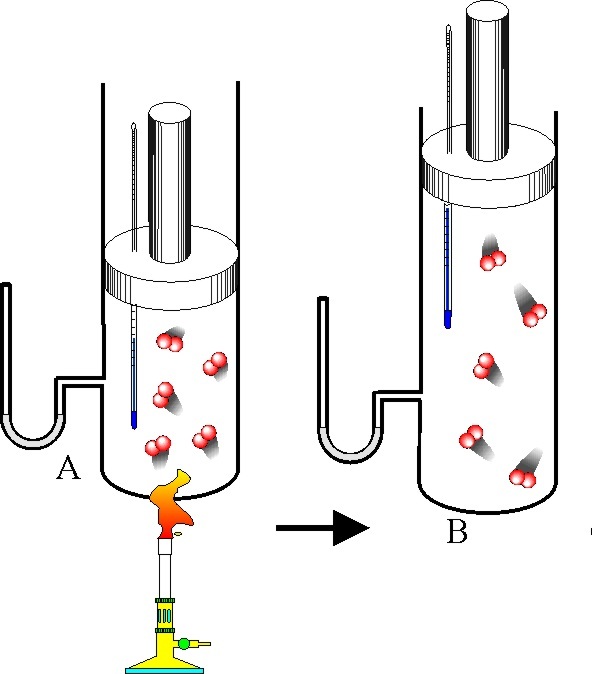
Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м3.
Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м3.
Изменение концентрации составило:
Δcn = cn2 – cn1 = 45,7 – 60,9 = -15,2 моль/м3.
Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.2. Уравнение состояния для газа в закрытом сосуде
При рассмотрении идеального газа, находящегося в закрытом сосуде (баллоне), необходимо учитывать, что изменение термодинамических параметров происходит при постоянной массе газа.
Для идеального газа, находящегося в закрытом сосуде, необходимо учитывать следующее:
- масса газа, находящегося в закрытом сосуде, вследствие изменения его термодинамических параметров не изменяется:
m = const;
- объем газа, заполняющего сосуд определенного объема, также фиксирован: V = const;
- постоянными также остаются следующие параметры газа:
ρ = const; ν = const; n = const;
где ρ – плотность газа; ν – количество вещества (газа); n – концентрация молекул (атомов) газа.
Для идеального газа, находящегося в закрытом сосуде и изменяющего свое состояние, уравнение Менделеева – Клапейрона записывается в виде системы (рис. 5.8):Рис. 5.8
p 1 V = ν R T 1 , p 2 V = ν R T 2 , }
где p 1, T 1 – давление и температура газа в начальном состоянии; p 2, T 2 – давление и температура газа в конечном состоянии; V – объем баллона; ν – количество газа; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Термин избыточное давление, встречающийся в задачах об идеальном газе в закрытом сосуде (баллоне), означает абсолютную разность между давлением газа, находящегося в сосуде, и давлением на стенки сосуда снаружи:
p изб = |p − p 0|,
где p – давление газа, находящегося внутри сосуда; p 0 – давление (атмосферное либо гидростатическое) на стенки сосуда снаружи.
Пример 13. Баллон рассчитан на максимальное избыточное давление 150 МПа. В него накачали газ при температуре 300 К до давления 120 МПа. Постепенно нагревая газ, баллон погружают в воду плотностью 1000 кг/м3 на глубину 1000 м. До какой максимальной температуры можно нагреть газ в баллоне, чтобы он не взорвался?
Решение. Запишем уравнение Менделеева – Клапейрона для двух состояний газа, находящегося в баллоне:
- в начале нагревания
p 1V = νRT 1;
- в конце нагревания
p 2V = νRT 2;
где p 1 – первоначальное давление газа в баллоне; p 2 – давление газа в баллоне в конце нагревания; V – объем газа (баллона), V = const; ν – количество вещества (газа) в баллоне; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 – температура газа в начале процесса; T 2 – температура газа в конце процесса.
Отношение уравнений
p 1 V p 2 V = ν R T 1 ν R T 2
позволяет определить давление газа в конце процесса:
p 2 = p 1 T 2 T 1 .
В условии задачи задано максимальное избыточное давление, определяемое формулой
p изб max = | p 2 − p 0 | ,
где p 0 – давление снаружи баллона; p 2 – давление газа внутри баллона.
При погружении баллона в воду с одновременным нагреванием указанные давления снаружи и внутри баллона определяются следующими формулами:
- снаружи (сумма атмосферного и гидростатического давлений) –
p 0 = p атм + p гидр = p атм + ρ0gh,
где p атм – атмосферное давление; p гидр – гидростатическое давление, p гидр = ρ0gh; ρ0 – плотность воды; g – модуль ускорения свободного падения; h – глубина погружения баллона;
- внутри (давление газа) –
p 2 = p 1 T 2 T 1 ,
где T 2 – максимальная температура газа (искомая величина).
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
p изб max = | p 1 T 2 T 1 − ρ 0 g h − p атм | ≈ | p 1 T 2 T 1 − ρ 0 g h | ,
так как p атм << ρ0gh, p атм << p 2.
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
p изб max = p 1 T 2 T 1 − ρ 0 g h , p изб max = ρ 0 g h − p 1 T 2 T 1 ,
из которых следуют две формулы для расчета искомой величины:
T 2 = T 1 ⋅ ρ 0 g h + p изб max p 1 , T 2 = T 1 ⋅ ρ 0 g h − p изб max p 1 .
Максимальному значению искомой температуры соответствует значение, рассчитанное по первой формуле:
T 2 = 300 ⋅ 1000 ⋅ 10 ⋅ 1000 + 150 ⋅ 10 6 120 ⋅ 10 6 = 400 К.
Чтобы баллон не взорвался, его можно погрузить на заданную глубину, одновременно нагревая до температуры 400 К.
Пример 14. Бутылка емкостью 0,75 л выдерживает максимальное избыточное давление 150 кПа. Из бутылки откачивают воздух и запечатывают некоторое количество твердого углекислого газа с молярной массой 44,0 г/моль. Атмосферное давление равно 100 кПа. Считая, что объем твердого углекислого газа пренебрежимо мал по сравнению с объемом бутылки, найти его максимальную массу, которая не вызовет взрыва бутылки при температуре 300 К?
Решение. Запишем уравнение Менделеева – Клапейрона для углекислого газа, находящегося в бутылке, после его превращения в газообразное состояние:
p V = m M R T ,
где p – давление углекислого газа в бутылке; V – объем газа (бутылки); m – масса углекислого газа в бутылке; M – молярная масса углекислого газа; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T – температура газа.
Записанное уравнение позволяет получить выражение для расчета давления газа внутри бутылки:
p = m R T V M .
В условии задачи задано максимальное избыточное давление, определяемое формулой
p изб max = | p − p 0 | ,
где p 0 – давление снаружи бутылки.
Указанные давления снаружи и внутри бутылки определяются следующим образом:
- снаружи (атмосферное давление) – p 0;
- внутри (давление углекислого газа) –
p = m R T V M ,
где m соответствует искомой величине – максимальной массе углекислого газа.
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
p изб max = | m R T V M − p 0 | .
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
p изб max = m R T V M − p 0 , p изб max = p 0 − m R T V M ,
из которых следуют две формулы для расчета искомой величины:
m = V M ( p 0 + p изб max ) R T , m = V M ( p 0 − p изб max ) R T .
Максимальному значению искомой массы соответствует значение, рассчитанное по первой формуле:
m = 0,75 ⋅ 10 − 3 ⋅ 44,0 ⋅ 10 − 3 ( 100 + 150 ) ⋅ 10 3 8,31 ⋅ 300 = 3,3 ⋅ 10 − 3 кг = 3,3 г .
Чтобы бутылка не взорвалась, в нее можно запечатать не более 3,3 г твердого углекислого газа.
Пример 15. В наличии имеется неограниченное количество баллонов объемом по 4,0 л, заполненных некоторым идеальным газом до давления 500 кПа. Баллоны предназначены для наполнения газом оболочки аэрозонда и их можно соединять между собой. Сколько баллонов с газом необходимо одновременно подсоединить к пустой оболочке аэрозонда объемом 800 дм3, чтобы наполнить ее до давления 100 кПа, равного атмосферному? Температура газа при заполнении оболочки не изменяется.
Решение. Для осуществления процесса, описанного в условии задачи, требуется определенное количество газа ν.
Необходимое количество газа заполняет следующий объем:
- в начале процесса (до заполнения оболочки)
V 1 = NV бал,
где N – количество баллонов; V бал – объем одного баллона, V бал = 4,0 л;
- в конце процесса (после заполнения оболочки)
V 2 = NV бал + V обол,
где V обол – объем оболочки, V обол = 800 дм3.
Указанное количество газа находится при давлении:
- в начале процесса (до заполнения оболочки) –
p 1 = 500 кПа
и совпадает с давлением газа в каждом из баллонов;
- в конце процесса (после заполнения оболочки) –
p 2 = 100 кПа
и совпадает с давлением в оболочке.
Считая процесс заполнения газом оболочки аэрозонда изотермическим, запишем уравнение Менделеева – Клапейрона следующим образом:
- в начале процесса (до заполнения оболочки) –
p 1V 1 = νRT,
где ν – количество вещества (газа) в оболочке; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T – температура газа (не изменяется в ходе процесса);
- в конце процесса (после заполнения оболочки) –
p 2V 2 = νRT.
Равенство
p 1V 1 = p 2V 2,
записанное в явном виде
p 1NV бал = p 2(NV бал + V обол),
позволяет получить формулу для вычисления искомого числа баллонов:
N = V обол V бал ⋅ p 2 p 1 − p 2 .
Произведем расчет:
N = 800 ⋅ 10 − 3 4,0 ⋅ 10 − 3 ⋅ 100 ⋅ 10 3 ( 500 − 100 ) ⋅ 10 3 = 50 .
Следовательно, для заполнения оболочки до указанного давления необходимо 50 баллонов с газом.
Пример 16. Аэростат, оболочка которого заполнена азотом с молярной массой 28 г/моль, находится в воздухе. Молярная масса воздуха равна 29 г/моль. Массы гондолы и оболочки аэростата пренебрежимо малы. Во сколько раз возрастет подъемная сила аэростата, если азот в его оболочке заменить на водород с молярной массой 2,0 г/моль, не изменяя при этом объем аэростата?
Решение. Силы (сила тяжести m g → и сила Архимеда F → A ), действующие на аэростат, показаны на рисунке.
Подъемная сила – это векторная сумма силы тяжести и силы Архимеда:
F → под = F → A + m g → ,
где F → A – сила Архимеда, действующая на оболочку со стороны воздуха; m g → – сила тяжести; m – масса газа, заполняющего оболочку аэростата; g → – ускорение свободного падения.
В проекциях на вертикальную ось подъемная сила определяется следующими выражениями:
- при заполнении оболочки азотом –
F под1 = F A1 − m 1g,
где F A1 – модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки азотом, F A1 = ρ0gV 1; ρ0 – плотность воздуха; V 1 – объем оболочки аэростата при заполнении ее азотом (объем воздуха, вытесненного оболочкой); m 1 – масса азота, заполняющего оболочку, m 1 = ρ1V 1; ρ1 – плотность азота;
- при заполнении оболочки водородом –
F под2 = F A2 − m 2g,
где F A2 – модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки водородом, F A2 = ρ0gV 2; V 2 – объем оболочки аэростата при заполнении ее водородом (объем воздуха, вытесненного оболочкой); m 2 – масса водорода, заполняющего оболочку, m 2 = ρ2V 2; ρ2 – плотность водорода.
Искомой величиной является отношение
F под 2 F под 1 = F A 2 − m 2 g F A 1 − m 1 g .
С учетом записанных выражений для сил Архимеда, масс азота и водорода, а также равенства объемов оболочки при заполнении ее азотом и водородом (V 1 = V 2), указанное отношение принимает вид
F под 2 F под 1 = ρ 0 g V 2 − ρ 2 V 2 g ρ 0 g V 1 − ρ 1 V 1 g = ( ρ 0 − ρ 2 ) V 2 g ( ρ 0 − ρ 1 ) V 1 g = ρ 0 − ρ 2 ρ 0 − ρ 1 .
Плотности воздуха, азота и водорода определим как отношения:
- для воздуха
ρ 0 = M 0 V μ 0 ,
где M 0 – молярная масса воздуха; V µ0 – молярный объем воздуха;
- для азота
ρ 1 = M 1 V μ 1 ,
где M 1 – молярная масса азота; V µ1 – молярный объем азота;
- для водорода
ρ 2 = M 2 V μ 2 ,
где M 2 – молярная масса водорода; V µ2 – молярный объем водорода.
Молярные объемы (объемы одного моля) воздуха, азота и водорода равны между собой, так как газы находятся при одних и тех же условиях:
V µ0 = V µ1 = V µ2 = V µ.
Поэтому формула для расчета искомого отношения приобретает вид
F под 2 F под 1 = ρ 0 − ρ 2 ρ 0 − ρ 1 = M 0 − M 2 M 0 − M 1 .
Расчет дает значение:
F под 2 F под 1 = 29 ⋅ 10 − 3 − 2,0 ⋅ 10 − 3 29 ⋅ 10 − 3 − 28 ⋅ 10 − 3 = 27 .
При замене азота на водород в оболочке аэростата его подъемная сила возрастет в 27 раз.
Пример 17. Воздушный шар с температурой 300 К находится в воздухе при атмосферном давлении 100 кПа. Молярная масса воздуха составляет 29,0 г/моль. Объем воздушного шара равен 830 дм3, а масса его оболочки равна 333 г. На сколько градусов необходимо нагреть газ в оболочке, чтобы шар взлетел? Воздух в оболочке шара сообщается с атмосферой.
Решение. Силы, действующие на воздушный шар, показаны на рисунке:
- сила Архимеда
F A = ρ0gV,
где ρ0 – плотность воздуха, окружающего шар; g – модуль ускорения свободного падения; V – объем оболочки шара (объем вытесненного оболочкой воздуха);
- сила тяжести
mg = (m обол + m возд)g,
где m обол – масса оболочки; m возд – масса воздуха в оболочке, m возд = ρV; ρ – плотность воздуха внутри оболочки.
Шар взлетает, когда выполняется равенство
F → A + m g → = 0,
или, в проекции на вертикальную ось, –
F A − mg = 0.
Преобразуем равенство (условие равновесия шара в воздухе)
F A = mg
с учетом записанных выше выражений
ρ0gV = (m обол + m возд)g, или (ρ0 − ρ)V = m обол.
Входящие в равенство плотности воздуха не известны, но фигурируют в качестве параметра в уравнении состояния:
- для воздуха снаружи оболочки воздушного шара
p 0 = ρ 0 R T 1 M ,
где p 0 – атмосферное давление; ρ0 – плотность воздуха снаружи оболочки; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 – температура окружающего шар воздуха; M – молярная масса воздуха;
- для воздуха внутри оболочки воздушного шара
p = ρ R T 2 M ,
где p – давление воздуха внутри оболочки; ρ – плотность воздуха внутри оболочки; T 2 – температура воздуха внутри оболочки.
Давления воздуха внутри и снаружи оболочки воздушного шара одинаковы, так как воздух, находящийся в оболочке, сообщается с атмосферой; поэтому
p = p 0.
Плотности:
- для воздуха снаружи оболочки воздушного шара
ρ 0 = p 0 M R T 1 ;
- для воздуха внутри оболочки воздушного шара
ρ = p 0 M R T 2 .
Подставим выражения для плотностей в условие равновесия шара в воздухе:
( 1 T 1 − 1 T 2 ) p 0 M V R = m обол .
Температура воздуха внутри оболочки, при которой шар начинает взлетать, определяется как
T 2 = p 0 M V T 1 p 0 M V − R T 1 m обол ,
а искомая разность –
Δ T = T 2 − T 1 = p 0 M V T 1 p 0 M V − R T 1 m обол − T 1 = T 1 p 0 M V R T 1 m обол − 1 .
Произведем вычисление:
Δ T = 300 100 ⋅ 10 3 ⋅ 29,0 ⋅ 10 − 3 ⋅ 830 ⋅ 10 − 3 8,31 ⋅ 300 ⋅ 333 ⋅ 10 − 3 − 1 = 158 К.
Следовательно, чтобы воздушный шар начал взлетать, воздух в его оболочке необходимо нагреть на 158 К, или 158 °С.
Пример 18. Камеру футбольного мяча объемом 3,00 л накачивают с помощью насоса, забирающего из атмосферы 0,150 л воздуха при каждом качании. Атмосферное давление составляет 100 кПа. Определить давление в камере после 30 качаний, если первоначально она была пустой. Температура постоянна.
Решение. За N качаний насос забирает из атмосферы определенное количество воздуха ν. Это же количество воздуха попадает в камеру футбольного мяча.
Указанное количество воздуха имеет следующий объем:
- воздух, забранный из атмосферы за N качаний насоса, –
V 1 = NV нас,
где V нас – объем насоса, V нас = 0,150 л; N – количество качаний;
- воздух, накачанный в камеру футбольного мяча, –
V 2 = V мяч,
где V мяч – объем камеры мяча, V мяч = 3,00 л.
Данное количество воздуха находится при следующем давлении:
- воздух, забранный из атмосферы за N качаний насоса, –
p 1 = 100 кПа
совпадает с атмосферным давлением;
- воздух, накачанный в камеру футбольного мяча, – p 2 (является искомой величиной).
Считая процесс заполнения воздухом камеры мяча изотермическим, запишем уравнение Менделеева – Клапейрона следующим образом:
- для воздуха, забранного из атмосферы за N качаний насоса, –
p 1V 1 = νRT,
где R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T – температура газа (не изменяется в ходе процесса);
- для воздуха, накачанного в камеру футбольного мяча, –
p 2V 2 = νRT.
Равенство
p 1V 1 = p 2V 2,
записанное в явном виде
p 1NV нас = p 2V мяч,
позволяет получить формулу для вычисления давления в камере футбольного мяча:
p 2 = p 1 N V нас V мяч .
Произведем вычисление:
p 2 = 100 ⋅ 10 3 ⋅ 30 ⋅ 0,15 ⋅ 10 − 3 3,00 ⋅ 10 − 3 = 150 ⋅ 10 3 Па = 150 кПа.
Источник
