Концентрация молекул в сосуде формула
В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.
Идеальный газ

Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.
Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.
Универсальное уравнение
Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
P * V = n * R * T.
Где R – постоянная, равная 8,314 Дж/(моль*К), n – количество вещества.
Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).
Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций
Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.
В случае газов, как правило, пользуются тремя следующими концентрациями:
- Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
- Массовая. Показывает отношение массы компонента к объему газа.
- Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.
Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.
Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.
Формула концентрации молекул газа
В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:
cn(i) = ni / V.
Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:
P * V = n * R * T =>
cn = n / V = P / (R * T).
Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
cn = n / V = N / (NA * V) = cN / NA =>
cN = cn * NA = NA * P / (R * T) = P / (kB * T).
Здесь NA и kB – число Авогадро и постоянная Больцмана. Соответственно, N – число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10-23), то cN принимает огромные значения, что неудобно для ее практического использования.
Пример задачи
В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.
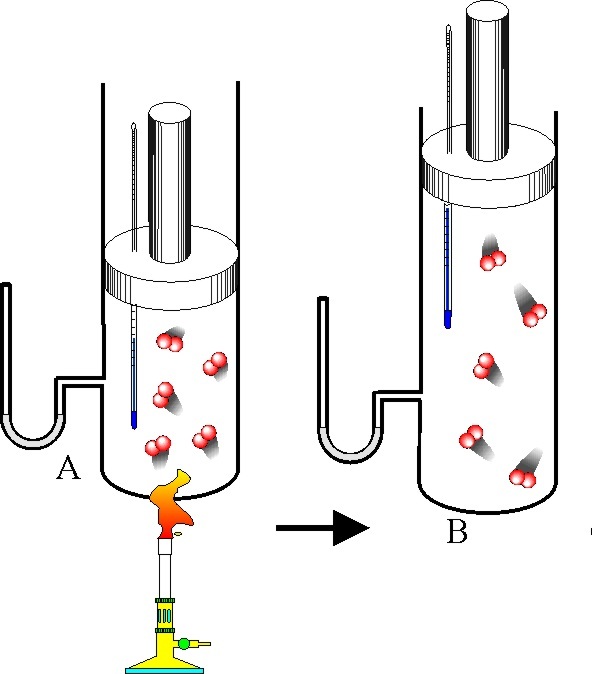
Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м3.
Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м3.
Изменение концентрации составило:
Δcn = cn2 – cn1 = 45,7 – 60,9 = -15,2 моль/м3.
Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.
Источник
9 апреля 2012
Автор КакПросто!
Концентрация частиц – это величина, показывающая, сколько частиц вещества находится в каком-либо объеме. Она вычисляется по формуле: c = N/V, ее размерность 1/м^3. Часто возникает необходимость определить концентрацию молекул, причем исследуемое вещество может быть в любом агрегатном состоянии: твердом, жидком или газообразном.
Инструкция
Представьте, что любознательный царь Гиерон дал своему придворному математику еще одну корону, приказав: «Вот она-то точно из чистого золота. Определи, Архимед, какова концентрация молекул в ней». Гениального ученого такая задача поставила бы в тупик. Ну, а вы решите ее очень быстро. Предположим, корона весила бы ровно 1,93 килограмма, занимая при этом объем в 100 см^3.
Прежде всего найдите, сколько молей золота содержится в таком количестве вещества. С помощью таблицы Менделеева вы узнаете молекулярную массу золота: 197 а.е.м. (атомных единиц массы). А масса одного моля любого вещества (в граммах) численно равна его молекулярной массе. Следовательно, один моль золота весит 197 грамм. Разделив фактическую массу короны на молярную массу золота, вы получите: 1930/197 = 9,79. Или, округленно, 9,8 молей золота.
Умножьте количество молей на универсальное число Авогадро, показывающее, сколько элементарных частиц содержится в моле любого вещества. 9,8*6,022*10^23 = 5,9*10^24. Вот сколько молекул золота приблизительно содержится в короне.
Ну, а теперь найти концентрацию молекул проще простого. 100 кубических сантиметров – это 0,0001 м^3. Разделим: 5,9*10^24/0,0001 = 5,9*10^28. Концентрация молекул золота равна 5,9*10^28/м3.
Теперь предположим, что вам задана такая задача: при давлении Р, средняя квадратичная скорость молекул углекислого газа равна V. Требуется определить концентрацию его молекул. И здесь нет ничего сложного. Существует так называемое основное уравнение кинетической теории идеального газа: Р = V^2m0C/3, где C – концентрация молекул газа, а m0 – масса одной его молекулы. Следовательно, искомая концентрация С находится так: С = 3P/m0V^2.
Единственная неизвестная величина – m0. Ее можно узнать в справочнике по химии или физике. Можно также вычислить по формуле: m0 = M/Na, где М – молярная масса углекислого газа (44 грамм/моль), а Na – число Авогадро (6,022х1023). Подставив все величины в формулу, вычислите искомую концентрацию С.
Видоизмените условие задачи. Предположим, вам известны только температура Т и давление Р углекислого газа. Как по этим данным найти концентрацию его молекул? Давление и температура газа связаны формулой: P = CkT, где С – концентрация молекул газа, а К – постоянная Больцмана, равная 1,38*10^-23. То есть С = P/kT. Подставив в формулу известные величины, вы вычислите концентрацию С.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Источник
Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.

Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
P*V = n*R*T.
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R – это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление

Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
cN = N/V.
Где N – общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
n = N/NA;
kB = R/NA.
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
P*V = n*R*T =>
P*V = N/NA*R*T = N*kB*T =>
cN = N/V = P/(kB*T).
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
cn = n/V = P/(R *T).
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 oC (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
cn(O2) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м3.
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*1021 молекул.
Источник
5.2. Основное уравнение молекулярно-кинетической теории
5.2.1. Термодинамические параметры газа и основные характеристики вещества
Для описания состояния идеального газа используют термодинамические параметры (температуру, давление, объем).
Температура T характеризует интенсивность теплового движения молекул. В Международной системе единиц температура измеряется в кельвинах (1 К). Термодинамическая (абсолютная) температура (в кельвинах, К) связана с температурой (в градусах Цельсия, °С) формулой
T = t + 273,
где T – термодинамическая (абсолютная) температура; t – температура по шкале Цельсия.
Давление p газа определяется числом упругих столкновений молекул со стенками сосуда и зависит от массы молекул газа, их средней скорости и концентрации в сосуде. В Международной системе единиц давление измеряется в паскалях (1 Па).
Объем V газа совпадает с объемом сосуда, в котором он находится, т.е. газ занимает весь предоставленный ему объем. В Международной системе единиц объем измеряется в кубических метрах (1 м3).
Один моль – это количество вещества, содержащее столько же молекул, сколько содержится атомов в 0,012 кг углерода. В Международной системе единиц количество вещества измеряется в молях (1 моль). В 1 моль любого вещества (не только идеального газа) содержится 6,02 ⋅ 1023 молекул (атомов).
Указанная величина является постоянной для любого вещества и имеет специальное название – число (постоянная) Авогадро:
N A = 6,02 ⋅ 1023 моль−1.
В Международной системе единиц постоянная Авогадро измеряется в обратных молях (1 моль−1).
Количество молекул (атомов) в некоторой массе вещества рассчитывается как произведение
N = νN A,
где ν – количество вещества, ν = m/M; m – масса вещества; M – молярная масса вещества; N A – постоянная Авогадро, N A ≈ 6,02 ⋅ 1023 моль−1.
Плотность вещества ρ рассчитывается как отношение
ρ = m V ,
где m – масса вещества, содержащегося в объеме V.
В Международной системе единиц плотность измеряется в килограммах, деленных на кубический метр (1 кг/м3).
Относительная молекулярная масса M r – это отношение массы молекулы данного вещества к 1/12 массы атома углерода:
M r = m 0 1 12 m C ,
где m 0 – масса одной молекулы данного вещества; m C – масса атома углерода.
Величина
1 12 m C = 1,66 ⋅ 10 − 27 кг = 1 a. e. м.
имеет специальное название – атомная единица массы.
Молярная масса M – это масса вещества, взятого в количестве 1 моль; она может быть рассчитана как:
1) отношение массы вещества к его количеству (в молях):
M = m ν ,
где m – масса вещества; ν – количество вещества;
2) произведение массы одной молекулы этого вещества на число Авогадро:
M = m 0N A,
где N A – постоянная Авогадро, N A ≈ 6,02 ⋅ 1023 моль−1.
В Международной системе единиц молярная масса измеряется в килограммах, деленных на моль (1 кг/моль).
Массу молекулы можно найти по одной из трех формул:
m 0 = m N ; m 0 = ρ n ; m 0 = M N A ,
где m – масса вещества; N – число частиц (атомов или молекул), содержащихся в указанной массе вещества; ρ – плотность вещества; n – концентрация вещества (число частиц в единице объема; измеряется в м‒3), n = N/V; V – объем, который занимает указанная масса вещества; M – молярная масса данного вещества; N A – постоянная Авогадро, N A ≈ 6,02 ⋅ 1023 моль−1.
Молярный объем (объем 1 моль вещества) определяется отношением
V μ = M ρ ,
где M – молярная масса вещества; ρ – плотность вещества.
При нормальных условиях (p = 101 325 Па = 760 мм рт. ст., t = 0 °С) молярный объем любого идеального газа составляет V μ = 22,4 л/моль.
Пример 1. Медь имеет молярную массу 63 г/моль, а ее плотность равна 8,4 г/см3. Найти объем 10 моль меди.
Решение. Объем меди определяется выражением
V = m ρ ,
где m – масса меди; ρ – плотность меди.
Массу меди найдем по формуле
m = νM,
где ν – количество вещества (меди); M – молярная масса меди.
Таким образом, искомый объем
V = ν M ρ .
Вычисление дает результат:
V = 10 ⋅ 63 ⋅ 10 − 3 8,4 ⋅ 10 3 = 75 ⋅ 10 − 6 м3 = 75 см3.
Пример 2. Плотности меди и свинца равны 8,40 и 13,0 г/см3, а молярные массы – 64,0 и 208 г/моль соответственно. Во сколько раз число атомов меди в 2,0 м3 больше числа атомов свинца в 0,20 м3?
Решение. Число атомов (молекул) в некотором количестве вещества определяется формулой
N = νN A,
где N A – постоянная (число) Авогадро, N A = 6,02 ⋅ 1023 моль−1; ν – количество вещества.
Количество вещества зависит от массы вещества и его молярной массы:
ν = m M ,
где m = ρV – масса вещества; ρ – плотность вещества; V – объем, который занимает данное вещество; M – молярная масса вещества.
Таким образом, количество атомов (молекул) некоторого вещества через характеристики, заданные в условии задачи, определяется выражением
N = ν N A = ρ V N A M .
Для меди и свинца полученная формула имеет следующий вид:
- для меди
N 1 = ρ 1 V 1 N A M 1 ,
где ρ1 – плотность меди; V 1 – объем, занятый медью; M 1 – молярная масса меди;
- для свинца
N 2 = ρ 2 V 2 N A M 2 ,
где ρ2 – плотность свинца; V 2 – объем, занятый свинцом; M 2 – молярная масса свинца.
Искомым является отношение
N 1 N 2 = ρ 1 V 1 N A M 1 ⋅ M 2 ρ 2 V 2 N A = ρ 1 ρ 2 ⋅ V 1 V 2 ⋅ M 2 M 1 .
Произведем вычисление:
N 1 N 2 = 8,40 ⋅ 10 3 13,0 ⋅ 10 3 ⋅ 2,0 0,20 ⋅ 208 ⋅ 10 − 3 64,0 ⋅ 10 − 3 = 21 .
Число атомов меди в 2,0 м3 больше числа атомов свинца в 0,20 м3 в 21 раз.
Пример 3. В озеро глубиной 50,0 м и площадью 100 км2 бросили кристаллик соли массой 10,0 мг. Соль, растворившись, равномерно распределилась в озере. Молярная масса соли равна 40,0 г/моль. Сколько молекул соли находится в 1,0 мм3 воды?
Решение. Количество молекул соли в заданной массе вещества определяется выражением
N = m M N A ,
где m – масса соли; M – молярная масса соли; N A – постоянная (число) Авогадро, N A = 6,02 ⋅ 1023 моль−1.
Используя данную формулу, определим концентрацию соли в озере (число молекул соли в единице объема воды):
n = N V = m N A M V ,
где V – объем озера, V = Sh; S – площадь озера; h – глубина озера.
С учетом выражения для объема данная формула выглядит следующим образом:
n = m N A M S h .
Расчет дает значение:
n = 10,0 ⋅ 10 − 6 ⋅ 6,02 ⋅ 10 23 40,0 ⋅ 10 − 3 ⋅ 100 ⋅ 10 6 ⋅ 50,0 = 30 ⋅ 10 9 м−3.
В Международной системе единиц объем измеряется в кубических метрах, т.е. в каждом кубическом метре воды из данного озера оказалось 30 ⋅ 109 молекул соли.
В каждом кубическом миллиметре содержится в 109 раз меньше молекул, т.е. концентрация молекул в пересчете на кубический миллиметр равна
n ′ = 30 ⋅ 10 9 10 9 = 30 мм−3.
Следовательно, в одном кубическом миллиметре оказалось 30 молекул соли.
Источник
