Конечное давление в сосуде
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
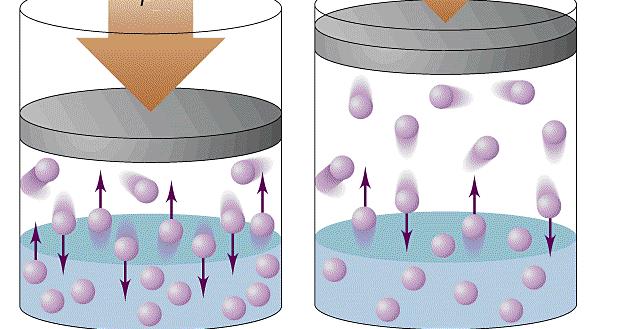
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Определение
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p – давление столба жидкости (Па), ρж- плотность жидкости (кг/м3), g – ускорение свободного падения (≈10 м/с2), h – высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
Сила давления жидкости на дно сосуда – это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда – это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором – керосин (ρ2 = 0,8 г/см3), в третьем – спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22709 Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18804
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 2.2k | Оценить:
Источник
Физика
При рассмотрении идеального газа, находящегося в открытом сосуде , необходимо учитывать, что вследствие изменения термодинамических параметров часть газа выходит из сосуда. При этом уравнение состояния записывается только для той части газа, которая остается в сосуде.
Для идеального газа, находящегося в открытом сосуде, необходимо учитывать следующее:
- масса газа изменяется в результате изменения его термодинамических параметров:
- рассматривается газ, оставшийся в сосуде определенного объема, т.е. объем газа фиксирован:
- давление газа может изменяться или оставаться постоянным (в зависимости от условия задачи), причем на изменение давления в условии задачи обычно бывает четкое указание.
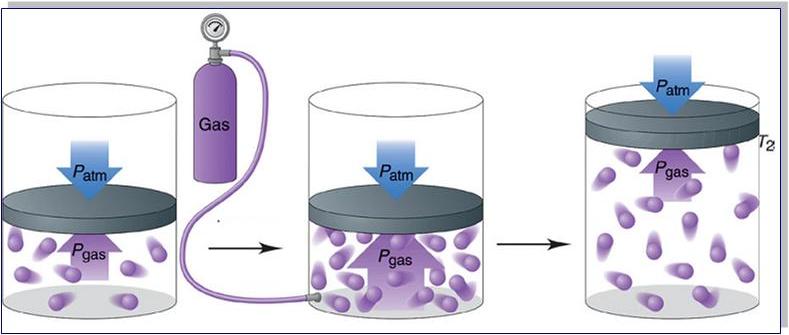
Если давление идеального газа в открытом сосуде по условию задачи изменяется ( p ≠ const), то уравнение Менделеева – Клапейрона записывается для двух состояний газа в виде системы (рис. 5.7):
Рис. 5.7
p 1 V = m 1 M R T 1 , p 2 V = m 2 M R T 2 , >
где p 1 , m 1 , T 1 – давление, масса и температура газа в начальном состоянии; p 2 , m 2 , T 2 – указанные параметры газа в конечном состоянии; V – объем сосуда; M – молярная масса газа; R – универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К).
Если давление идеального газа в открытом сосуде по условию задачи остается постоянным ( p = const), то изменения некоторых характеристик газа в открытом сосуде можно вычислить по следующим формулам:
Δ m = m 1 − m 2 = m 1 ( 1 − T 1 T 2 ) ,
где m 1 – первоначальная масса газа; m 2 – масса газа в конце процесса; T 1 – термодинамическая (абсолютная) температура газа в начале процесса; T 2 – термодинамическая (абсолютная) температура газа в конце процесса;
Δ ρ = ρ 1 − ρ 2 = ρ 1 ( 1 − T 1 T 2 ) ,
где ρ 1 – первоначальная плотность газа; ρ 2 – плотность газа в конце процесса;
- изменение количества вещества
Δ ν = ν 1 − ν 2 = ν 1 ( 1 − T 1 T 2 ) ,
где ν 1 – первоначальное количество вещества (газа) в сосуде; ν 2 – количество вещества (газа) в сосуде в конце процесса.
Пример 11. В открытом сосуде объемом 450 дм 3 содержится некоторое количество идеального газа. Температуру газа увеличивают от 27 до 177 °С. Давление газа остается постоянным и равным 166 кПа. Сколько моль газа выйдет из сосуда?
Решение . Запишем уравнение Менделеева – Клапейрона для двух состояний газа, находящегося в открытом сосуде, при нагревании:
- для начального состояния
- для конечного состояния
где p – давление газа, p = const; V – объем газа (сосуда), V = const; ν 1 , ν 2 – количество вещества (газа) в начале и в конце процесса; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 , T 2 – температура газа в начале и в конце процесса.
Первое уравнение позволяет получить формулу для расчета количества вещества (газа) в начале процесса:
Подстановка полученной формулы в уравнение
Δ ν = ν 1 ( 1 − T 1 T 2 )
дает искомую разность
Δ ν = p V R T 1 ( 1 − T 1 T 2 ) = p V ( T 2 − T 1 ) R T 1 T 2 .
Для вычисления искомой величины необходимо перевести температуру из градусов Цельсия в кельвины:
T 1 = t 1 + 273 = 27 + 273 = 300 К,
T 2 = t 2 + 273 = 177 + 273 = 450 К.
Δ ν = 166 ⋅ 10 3 ⋅ 450 ⋅ 10 − 3 ( 450 − 300 ) 8,31 ⋅ 450 ⋅ 300 = 10 моль.
При нагревании из сосуда вышло 10 моль газа.
Пример 12. В баллоне при температуре 15 °С находится идеальный газ. Из баллона выходит 40 % газа, а температура при этом понижается на 8,0 °С. Во сколько раз уменьшится давление газа в баллоне?
Решение . Запишем уравнение Менделеева – Клапейрона для двух состояний газа, находящегося в открытом сосуде:
- для начального состояния
p 1 V = ν 1 RT 1 ;
- для конечного состояния
p 2 V = ν 2 RT 2 ;
где p 1 – давление газа в начальном состоянии; p 2 – давление газа в конечном состоянии; V – объем газа (сосуда), V = const; ν 1 , ν 2 – количество вещества (газа) в начале и в конце процесса соответственно; R – универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T 1 , T 2 – температура газа в начале и в конце процесса соответственно.
Искомой величиной является отношение давлений p 1 / p 2 , которое определим из отношения уравнений:
p 1 V p 2 V = ν 1 R T 1 ν 2 R T 2 , т.е. p 1 p 2 = ν 1 T 1 ν 2 T 2 .
В результате процесса из баллона выходит 40 % газа, поэтому количество вещества (газа) ν 2 , оставшегося в баллоне, составляет 60 % от количества вещества (газа) ν 1 , которое было в начале процесса:
Для вычисления искомой величины необходимо сделать перевод температуры, заданной в градусах Цельсия, в кельвины:
T 1 = t 1 + 273 = 15 + 273 = 288 К,
T 2 = t 2 + 273 = ( t 1 − Δ t ) + 273 = (15 − 8,0) + 273 = 280 К.
Подстановка температур и количества вещества (газа), оставшегося в баллоне, в выражение для искомой величины дает
p 1 p 2 = ν 1 T 1 0,6 ν 1 T 2 = T 1 0,6 T 2 = 288 0,6 ⋅ 280 = 1,7 .
Давление газа в баллоне понизится в 1,7 раза.
Источник
Energy
education
сайт для тех, кто хочет изучать энергетику
Термодинамика и тепломассообмен
Основные законы термодинамики
Современная феноменологическая термодинамика является строгой теорией, развиваемой на основе нескольких постулатов. Процессы, происходящие в термодинамических системах, описываются макроскопическими величинами (температура, давление, концентрации компонентов), которые вводятся для описания систем, состоящих из большого числа частиц, и не применимы к отдельным молекулам и атомам, в отличие, например, от величин, вводимых в механике или электродинамике.
Примеры решения задач по теме «Процессы изменения состояния идеальных газов»
1. В закрытом сосуде емкостью $V = 300$ л содержится $3$ кг газа при давлении $p_1 = 8$ ат и температуре $t_1 = 20$ °C. Определить давление (ат) и удельный объем после охлаждения воздуха до $0$ °C.
2. В закрытом сосуде заключен газ при разрежении $p_1 = 6.7$ кПа и температуре $t_1 = 70$ °C. Показания барометра – $742$ мм.рт.ст. До какой температуры нужно охладить газ при том же атмосферном давлении, чтобы разрежение стало $p_2 = 13.3$ кПа?
3. В закрытом сосуде емкостью $V = 0.6$ м 3 содержится азот при давлении (абсолютном) $p_1 = 0.5$ МПа и температуре $t_1 = 20$ °C. В результате охлаждения сосуда азот, содержащийся в нем, теряет $105$ кДж. Определить, какие давление и температура устанавливаются в сосуде после охлаждения.
4. Сосуд емкостью $90$ л содержит углекислый газ при абсолютном давлении $0.8$ МПа и температуре $30$ °C. Определить количество теплоты, которое необходимо сообщить газу при $v = const$, чтобы давление поднялось до $1.6$ МПа.
5. Какое количество теплоты необходимо затратить, чтобы нагреть $2$ м 3 воздуха при постоянном избыточном давлении $p = 2$ ат от $t_1 = 120$ °C до $t_2 = 450$ °C? Какую работу при этом совершит воздух? Атмосферное давление принять равным $750$ мм.рт.ст., учесть зависимость теплоемкости от температуры.
6. В установке воздушного отопления внешний воздух при $t_1 = – 15$ °C нагревается в калорифере при $p = const$ до $60$ °C. Какое количество теплоты надо затратить для нагревания $1000$ м 3 наружного воздуха? Давление воздуха считать равным $755$ мм.рт.ст.
7. Уходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов $t_ = 300$ °C, конечная $t_ = 160$ °C; расход газов равен $900$ кг/ч. Начальная температура воздуха составляет $t_ = 15$ °C, а расход его равен $800$ кг/ч. Определить температуру нагретого воздуха $t_$, если потери тепла в воздухоподогревателе составляет $4$ %. Средние теплоемкости для газов и воздуха принять соответственно равными $1.0467$ и $1.0048$ кДж/(кгּ К).
8. При сжигании в топке парового котла каменного угля объем продуктов сгорания составляет $V_н = 11.025$ м 3 /кг (объем при нормальных условиях, приходящийся на 1 кг топлива). Анализ продуктов сгорания показывает следующий их объемный состав: $CO = 10$ %; $O2 = 8$ %; $H2O = 10$ %; $N2 = 72$ %. Определить количество теплоты, теряемой с уходящими газами (в расчете на $1$ кг топлива), если на выходе из котла температура газов равна $180$ °C, а температура окружающей среды $20$ °C. Давление продуктов сгорания принять равным атмосферному. Учесть зависимость теплоемкости от температуры.
9. Воздух в количестве $1$ кг при температуре $t = 30$ °C и начальном давлении $p_1 = 0.1$ МПа изотермически сжимается до конечного давления $p_2 = 1$ МПа. Определить конечный объем, затрачиваемую работу изменения объема и количество теплоты, отводимой от газа.
10. Воздух в количестве $12$ кг при температуре $t = 27$ °C изотермически сжимается до тех пор, пока давление не становится равным $4$ МПа. На сжатие затрачивается работа $L = -6$ МДж. Найти начальные давление и объем, конечный объем и теплоту, отведенную от воздуха.
11. Воздух в количестве $0.5$ кг изотермически расширяется от давления $p_1 = 100$ ат до $p_2$. Определить давление $p_2$ в ат, работу изменения объема $L_$ и отведенную теплоту $Q_$, если $frac= 5$ и $t_1 = 30$ °C.
12. В идеально охлаждаемом компрессоре происходит изотермическое сжатие углекислого газа. В компрессор поступает $700$ м 3 /ч газа (приведенного к нормальным условиям) при $p_1 = 0.095$ МПа и $t_1 = 47$ °C. Давление за компрессором $p_2 = 0.8$ МПа. Найти теоретическую мощность приводного двигателя $N_0$ (кВт) и теоретический расход $M_в$ охлаждающей компрессор воды (в кг/ч), если она нагревается в системе охлаждения на $Δt = 15$ °C.
13. Воздух при температуре $t_1 = 20$ °C должен быть охлажден посредством адиабатного расширения до температуры $t_2 = -30$ °C. Конечное давление воздуха при этом должно составлять $0.1$ МПа. Определить начальное давление воздуха $p_1$ и работу расширения $1$ кг воздуха.
14. Воздух при температуре $120$ °C изотермически сжимается так, что его объем становится равным $0.25$ начального, а затем расширяется по адиабате до начального давления. Определить температуру воздуха в конце адиабатного расширения. Представить процессы расширения и сжатия в диаграммах pv и Ts.
15. При адиабатном расширении $1$ кг воздуха $K = 1.40 = сonst$ температура его падает на $100$ K. Какова полученная в процессе расширения работа и сколько теплоты следовало бы подвести к воздуху, чтобы ту же работу получить в изотермическом процессе?
16. Воздух в количестве $1$ кг политропно расширяется от $12$ до $2$ ат, причем объем его увеличился в $4$ раза; начальная температура воздуха равна $120$ °C. Определить показатель политропы, начальный и конечный объемы, конечную температуру и работу расширения.
17. При политропном сжатии $1$ кг воздуха до объема $v_2 = 0.1ּ v_1$ температура поднялась с $10$ до $90$ °C. Начальное давление равно $0.8$ бар; $R = 287$ Дж/(кгּ K). Определить показатель политропы, конечные параметры газа, работу сжатия и количество отведенной наружу теплоты.
18. Воздух в компрессоре сжимается по политропе $n = 1.25$ от $1$ до $8$ бар; начальная температура воздуха $5$ °C. После сжатия воздух проходит через холодильник, охлаждаемый холодной водой, начальная температура которой $t_1 = 10$ °C, а конечная равна $t_2 = 18$ °C. Определить часовой расход охлаждающей воды, если производительность компрессора $1000$ мн 3 /ч при нормальных физических условиях, а воздух в холодильнике изобарно охлаждается до $30$ °C.
19. В воздушном двигателе воздух в количестве $1$ кг расширяется от $p_1 = 10$ ат до $p_2 = 1$ ат. Расширение может произойти изотермически, адиабатно и политропно с показателем политропы $n = 1.2$. Сравнить работы расширения и определить конечные параметры воздуха по этим трем процессам; начальная температура воздуха $t_1 = 227$ °C. Представить процессы на диаграмме pv.
20. В процессе политропного расширения воздуху сообщается $70$ кДж теплоты. Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в $8$ раз, а давление его уменьшилось в $10$ раз.
Администратор сайта: Колосов Михаил
:
Copyright © 2011-2020. All rights reserved.
Источник
Источник
