Кубический сосуд с непрозрачными стенками расположен так
Условие задачи:
Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит заднюю вертикальную стенку. Сколько воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет, находящийся на расстоянии 10 см от задней стенки сосуда на его дне? Ребро сосуда 40 см.
Задача №10.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(l=10) см, (a=40) см, (V-?)
Решение задачи:
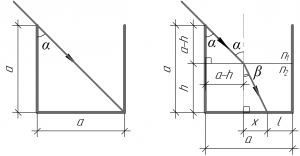Разумеется, сначала нужно сделать рисунки к задаче. Рассмотрим рисунок слева, он поможет нам найти угол падения луча (alpha). Так как сосуд имеет форму куба, то синус угла (alpha) можно найти следующим образом:
[sin alpha = frac{a}{{sqrt {{a^2} + {a^2}} }}]
[sin alpha = frac{{sqrt 2 }}{2};;;;(1)]
Теперь займемся правым рисунком. Из равенства (1) следует, что угол (alpha) равен 45°, и это очень важный вывод. Значит в прямоугольном треугольнике, образованном лучом, стенкой сосуда и поверхностью воды, оба катета равны (left( {a – h} right)) (смотрите рисунок справа).
Для ситуации на рисунке справа запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin alpha = {n_2}sin beta;;;;(2)]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.
Попытаемся найти синус угла (beta), для чего найдем противолежащий катет (x) в соответствующем прямоугольном треугольнике.
[x = a – l – left( {a – h} right)]
[x = h – l]
Сделаем важную оговорку: так как (x) не может быть меньше нуля, то ({h} > {l}), это пригодится нам в дальнейшем решении.
Тогда синус угла (beta) найдем по формуле (гипотенузу в том же прямоугольном треугольнике найдем по теореме Пифагора):
[sin beta = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }};;;;(3)]
Подставим в уравнение (2) выражения (1) и (3):
[frac{{sqrt 2 {n_1}}}{2} = frac{{{n_2}left( {h – l} right)}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Как Вы должны понимать, физика в этой задаче закончилась, осталась только математика – нужно решить данное уравнение. Перепишем его в следующем виде:
[frac{{sqrt 2 {n_1}}}{{2{n_2}}} = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Возведем в квадрат обе части этого уравнения:
[frac{{n_1^2}}{{2n_2^2}} = frac{{{{left( {h – l} right)}^2}}}{{{{left( {h – l} right)}^2} + {h^2}}}]
Перемножим “крест-накрест”:
[n_1^2{left( {h – l} right)^2} + n_1^2{h^2} = 2n_2^2{left( {h – l} right)^2}]
Раскроем скобки в обеих частях уравнения:
[n_1^2{h^2} – 2n_1^2hl + n_1^2{l^2} + n_1^2{h^2} = 2n_2^2{h^2} – 4n_2^2hl + 2n_2^2{l^2}]
Перенесем все в правую часть и сгруппируем:
[left( {2n_2^2 – 2n_1^2} right){h^2} – left( {4n_2^2 – 2n_1^2} right)hl + left( {2n_2^2 – n_1^2} right){l^2} = 0]
Поделим все на (l^2):
[left( {2n_2^2 – 2n_1^2} right){left( {frac{h}{l}} right)^2} – left( {4n_2^2 – 2n_1^2} right)left( {frac{h}{l}} right) + left( {2n_2^2 – n_1^2} right) = 0]
Решим данное квадратное уравнение относительно (frac{h}{l}), для чего перейдем к нахождению дискриминанта:
[D = {left( {4n_2^2 – 2n_1^2} right)^2} – 4left( {2n_2^2 – 2n_1^2} right)left( {2n_2^2 – n_1^2} right)]
Раскрываем скобки:
[D = 16n_2^4 – 16n_1^2n_2^2 + 4n_1^4 – 16n_2^4 + 8n_1^2n_2^2 + 16n_1^2n_2^2 – 8n_1^4]
[D = 8n_1^2n_2^2 – 4n_1^4]
[D = 4n_1^2left( {2n_2^2 – n_1^2} right)]
Учитывая численные значения показателей преломления, нетрудно сделать вывод, что дискриминант – положительный. Тогда корни уравнения следующие:
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm sqrt {4n_1^2left( {2n_2^2 – n_1^2} right)} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
Посчитаем численное значение корней:
[left[ begin{gathered}
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 2,686 hfill \
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} – 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 0,614 hfill \
end{gathered} right.]
Как Вы видите, второй корень не удовлетворяют условию ({h} > {l}). Значит уровень воды (h) равен:
[h = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right)l]
Искомый объем воды легко найти по формуле:
[V = {a^2}h]
Окончательно получим:
[V = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right){a^2}l]
[V = left( {frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}}} right) cdot {0,4^2} cdot 0,1 = 0,043;м^3 = 43;л]
Ответ: 43 л.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Практическое занятие № 5
Тема. Решение задач по теме “Законы отражения и преломления света. Полное внутреннее отражение”.
Цель:
- – на примерах решения задач на основные законы геометрической оптики рассмотреть основные типы задач, приемы и методы их решения.
Ход занятия
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности.
Прежде чем приступить к выполнению задания, необходимо повторить основные законы геометрической оптики и определения: луч падающий, отраженный, преломленный, углы падения, отражения, преломления, абсолютный и относительный показатели преломления, явление полного внутреннего отражения.
Получите основные законы геометрической оптики (законы преломления, отражения), применяя принцип Гюйгенса-Френеля для волн на границе двух сред.
Обратите внимание, что законы геометрической оптики и волновой оптики проявляются в физике при определенных физических условиях и имеют свои границы применимости.
Качественные задачи
- В ясные солнечные дни на загородных асфальтированных шоссе водители часто наблюдают “миражи”: некоторые участки асфальта, находящиеся впереди автомашины на расстоянии 80-100 м, кажутся покрытыми лужами. При приближении лужи исчезают и снова появляются впереди на других местах примерно на том же расстоянии. Как объясняется это явление?
- Луч света падает нормально на границу раздела двух сред. Чему равен угол отражения луча в градусах?
- Всегда ли световые лучи распространяются в среде прямолинейно?
- Если с самолета, летящего над морем, смотреть на поверхность моря, то непосредственно внизу она более темная, чем вдали. Как это можно объяснить?
- Луч света проходит через три прозрачные среды с показателями преломления n1, n2 и n3 (рис. 1). Каково соотношение между показателями преломления сред?
- В центре полого толстостенного шара из стекла находится точечный источник света. Будут ли преломляться световые лучи, распространяясь от источника через стенки шара?
- Световой луч проходит в вакууме расстояние S1 = 30 см, а в прозрачной жидкости за это же время расстояние S2 = 0,25 м. Определите показатель преломления жидкости.
Примеры решения расчетных задач
Задача 1. Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит стенку CD. До какой высоты h надо заполнить сосуд водой (n = 4/3), чтобы наблюдатель смог увидеть предмет F, находящийся на расстоянии b = 10 см от точки D?
Решение:
Так как, согласно условию задачи, глаз не видит дна сосуда, а сосуд имеет форму куба, угол падения луча зрения на поверхность жидкости равен α = 45° (рис. 2).
Из прямоугольного треугольника NKF видно, что .
Отсюда . (1)
Согласно закону преломления .
Тогда
; . (2)
После подстановки (2) в (1) получим:
Ответ:
Задача 2. Световой луч распространяется в стекле с показателем преломления n = 1,5. На его пути встречается щель, заполненная воздухом. Грани щели плоские и параллельные, расстояние между гранями равно d = 3 см, угол падения луча на грань α = 30°. На какое расстояние сместится световой луч, вышедший из щели, относительно продолжения падающего луча?
Решение:
Из прямоугольного треугольника ADC (рис. 3) видно, что боковое смещение луча равно h = AC·sin(r – α).
Из прямоугольного треугольника АВС выразим АС:
.
Согласно закону преломления , где n0 – показатель преломления воздуха (n0 = 1 ).
Отсюда . Тогда
см.
Ответ: .
Задача 3. На дне стеклянной ванны лежит зеркало, поверх которого налит слой воды высотой d = 20 см. В воздухе на высоте l = 30 см над поверхностью воды висит лампа. На каком расстоянии от поверхности воды смотрящий в воду наблюдатель увидит изображение лампы в зеркале? Показатель преломления воды n = 1,33.
Решение:
Для построения изображения S´ выберем два луча (рис. 4). Луч 1, направленный из точки S по нормали к поверхности воды, не преломляется. Луч 2, направленный под небольшим углом i к нормали, в точке К преломляется. Обозначим угол преломления через r. Преломленный луч падает на зеркало З в точку D под углом i, отражается от зеркала под углом r и на границе вода-воздух в точке С выходит под углом i к нормали. На пересечении луча 1 и продолжения луча 2 в точке S´ находится мнимое изображение точки S.
Из прямоугольного треугольника S´ОС выразим h:
.
Из прямоугольного треугольника SOK получим OK = l · tg i. Из треугольника KCD получим KC = 2d · tg r. Тогда
.
Так как для малых углов tg i ≈ sin i, то , тогда
.
Ответ:.
Задача 4. На нижней стороне плоскопараллельной стеклянной пластинки нанесена чернилами точка, которую наблюдатель видит на расстоянии h = 5 см от верхней поверхности. Определите толщину d пластинки, если луч зрения перпендикулярен к поверхности пластинки, показатель преломления стекла n = 1,6. Считать для малых углов
sin α ≈ tg α ≈α.
Решение:
Чернильное пятно, находящееся в точке А на нижней стороне стеклянной пластинки, рассматривается сверху и, как видно из рис. 5, кажется находящимся в точке A´. Поясним это. Направим в точку А два луча: луч 1 идет по нормали, не преломляясь. Луч 2, направленный под небольшим углом α, преломляется. Обозначим угол преломления через i. Преломленный луч падает в точку В под углом преломления i и выходит из пластинки под углом α. Чернильное пятно кажется находящимся на пересечении луча 1 и продолжения луча 2, проведенного из точки В в точку A´.
Из прямоугольного треугольника АВС видно, что . Из прямоугольного треугольника A´ВС: BC = h · tg α. После подстановки ВС получим для d:
.
Задача 5. В воду опущен прямоугольный стеклянный клин с показателем преломления стекла n = 1,5. При каком минимальном значении угла α (рис. 6) луч света, падающий нормально на грань АВ, достигнет грани АЕ? Под каким углом β он выйдет из призмы?
Решение:
Чтобы луч света полностью вышел из призмы, необходимо, чтобы он падал на грань ВЕ в точке падения С под углом αпред, который по построению равен искомому углу призмы α (рис. 7). В соответствии с законом преломления
Отсюда sin αпред = 0,8888, αпред = α = 62°30´.
Из треугольника CDE, используя свойство, что сумма углов треугольника равна 180°, найдем угол I = 2α – 90°. Снова воспользуемся законом преломления ,
откуда , β ≈ 40°19´.
Ответ: α = 62°30´; β = 40°19´.
Задачи для самостоятельной работы
- Точечный источник S расположен на расстоянии h = 1,5 см от передней поверхности плоскопараллельной пластинки толщиной d = 1,2 см, посеребренной с задней стороны. На каком расстоянии х от источника находится его изображение, получающееся в результате отражения лучей от задней поверхности пластинки? Показатель преломления вещества пластинки n = 1,6. Наблюдение производится по направлению, перпендикулярному к пластинке, под малыми углами..
Ответ:.
- На горизонтальном дне бассейна лежит плоское зеркало. Луч света, преломившись на поверхности воды, отражается от зеркала и выходит в воздух на расстоянии d = 1,5 м от места вхождения. Глубина бассейна h = 2 м, показатель преломления воды n = 1,33. Определите угол падения луча α.
Ответ: α ≈ 28°.
- Сечение стеклянной призмы имеет форму равностороннего треугольника. Луч падает на одну из граней по нормали к ней. Найдите угол φ между падающим лучом и лучом, вышедшим из призмы. Показатель преломления стекла n = 1,5.
Ответ: φ = 120°.
- Параллельный пучок света падает на поверхность воды под углом α = 60°. Ширина пучка в воздухе h = 5 см. Определите ширину пучка в воде, показатель преломления которой n = 1,33.
Ответ: 7,6 см.
- При каких значениях показателя преломления прямоугольной призмы возможен ход луча, изображенный на рис. 8? Сечение призмы – равнобедренный треугольник, луч падает на грань АС нормально.
Ответ: n > 1,41.
Рекомендуемая литература
- Касьянов В.А. Физика. 11 кл.: Учебн. для общеобразоват. учреждений. – 2-е изд., дополн. – М.: Дрофа, 2004. – С. 281-306.
- Элементарный учебник физики /Под ред акад. Г.С. Ландсберга. – Т. 3. – М.: Физматлит, 2000 и предшествующие издания.
- Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Электродинамика. Оптика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 308-334.
- Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 215-237.
- Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараева И.М. Задачи по элементарной физике. – М.: Физматлит, 2000 и предшествующие издания.
Источник
Опубликовано 10 месяцев назад по предмету
Физика
от idana19
Не тот ответ, который вам нужен?
Найди нужный
Самые новые вопросы
Математика – 10 месяцев назад
Сколько здесь прямоугольников
История – 1 год назад
Какое управление было в древнейшем риме? как звали первого и последнего из царей рима?
Литература – 1 год назад
Уроки французского ответе на вопрос : расскажите о герое по следующему примерному плану: 1.почему мальчик оказался в райцентре ? 2.как он чувствовал себя на новом месте? 3.почему он не убежал в деревню? 4.какие отношения сложились у него с товарищами? 5.почему он ввязался в игру за деньги? 6.как характеризуют его отношения с учительницей ? ответе на эти вопросы пожалуйста ! сочините сочинение пожалуйста
Русский язык – 1 год назад
Помогите решить тест по русскому языку тест по русскому языку «местоимение. разряды местоимений» для 6 класса
1. укажите личное местоимение:
1) некто
2) вас
3) ни с кем
4) собой
2. укажите относительное местоимение:
1) кто-либо
2) некоторый
3) кто
4) нам
3. укажите вопросительное местоимение:
1) кем-нибудь
2) кем
3) себе
4) никакой
4. укажите определительное местоимение:
1) наш
2) который
3) некий
4) каждый
5. укажите возвратное местоимение:
1) свой
2) чей
3) сам
4) себя
6. найдите указательное местоимение:
1) твой
2) какой
3) тот
4) их
7. найдите притяжательное местоимение:
1) самый
2) моего
3) иной
4) ничей
8. укажите неопределённое местоимение:
1) весь
2) какой-нибудь
3) любой
4) этот
9. укажите вопросительное местоимение:
1) сколько
2) кое-что
3) она
4) нами
10. в каком варианте ответа выделенное слово является притяжательным местоимением?
1) увидел их
2) её нет дома
3) её тетрадь
4) их не спросили
Русский язык – 1 год назад
Переделай союзное предложение в предложение с бессоюзной связью.
1. океан с гулом ходил за стеной чёрными горами, и вьюга крепко свистала в отяжелевших снастях, а пароход весь дрожал.
2. множество темноватых тучек, с неясно обрисованными краями, расползались по бледно-голубому небу, а довольно крепкий ветер мчался сухой непрерывной струёй, не разгоняя зноя
3. поезд ушёл быстро, и его огни скоро исчезли, а через минуту уже не было слышно шума
Русский язык – 1 год назад
помогите прошу!перепиши предложения, расставляя недостающие знаки препинания. объясни, что соединяет союз и. если в предложении один союз и, то во втором выпадающем списке отметь «прочерк».пример:«я шёл пешком и,/поражённый прелестью природы/, часто останавливался».союз и соединяет однородные члены.ночь уже ложилась на горы (1) и туман сырой (2) и холодный начал бродить по ущельям.союз и соединяет:1) части сложного предложенияоднородные члены,2) однородные членычасти сложного предложения—.поэт — трубач зовущий войско в битву (1) и прежде всех идущий в битву сам (ю. янонис).союз и соединяет:1) части сложного предложенияоднородные члены,2)
Физика – 1 год назад
Вокруг прямого проводника с током (смотри рисунок) существует магнитное поле. определи направление линий этого магнитного поля в точках a и b.обрати внимание, что точки a и b находятся с разных сторон от проводника (точка a — снизу, а точка b — сверху). рисунок ниже выбери и отметь правильный ответ среди предложенных.1. в точке a — «от нас», в точке b — «к нам» 2. в точке a — «к нам», в точке b — «от нас» 3. в обеих точках «от нас»4. в обеих точках «к нам»контрольная работа по физике.прошу,не наугад важно
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
Ответ
Ответ дан
valeravolkogonov
Ответ:
Ответ:27 см
Объяснение: