Малый поршень в сообщающемся сосуде
Определение и принцип гидравлического пресса
Определение
Гидравлический пресс – это машина, которая действует на основе законов движения и равновесия жидкостей.
Закон Паскаля лежит в основе принципа действия гидравлического пресса. Название этого устройства происходит от греческого слова гидравликос – водяной. Гидравлическим прессом называют гидравлическую машину, которая используется для прессования (сдавливания). Гидравлический пресс используют там, где необходима большая сила, например, при выдавливании масла из семян. При помощи современных гидравлических прессов можно получать силу до ${10}^8$ньютонов.
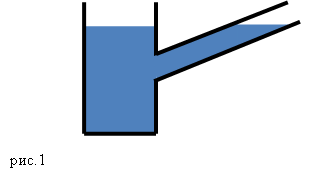
Основу гидравлической машины составляют два цилиндра разного радиуса с поршнями (рис.1), которые соединены трубой. Пространство в цилиндрах под поршнями обычно заполняют минеральным маслом.
Для того чтобы понять принцип действия гидравлической машины следует вспомнить, что такое сообщающиеся сосуды и в чем смысл закона Паскаля.
Сообщающиеся сосуды
Сообщающимися называют сосуды, соединенные между собой и в которых жидкость может свободно перетекать из одного сосуда в другой. Форма сообщающихся сосудов может быть разной. В сообщающихся сосудах жидкость одной плотности устанавливается на одном уровне, если давления над свободными поверхностями жидкости одинаковы.
Из рис.1 мы видим, что конструктивно гидравлическая машина – это два сообщающихся сосуда разного радиуса. Высоты столбов жидкости в цилиндрах будут одинаковыми, если на поршни не действуют силы.
Закон Паскаля
Закон Паскаля говорит нам о том, что давление, которое оказывают внешние силы на жидкость, передаются ей без изменения во все ее точки. На законе Паскаля основано действие многих гидравлических устройств: прессов, тормозных систем, гидроприводов, гидроусилителей и т.д.
Принцип действия гидравлического пресса
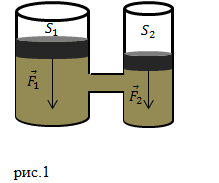
Одним из самых простых и старых устройств основанных на законе Паскаля является гидравлический пресс, в котором небольшая сила $F_1$, прикладываемая к поршню небольшой площади $S_1$, преобразуется в большую силу $F_2$, которая воздействует на площадь большой площади $S_2$.
Давление, которое создает поршень номер один, равно:
[p_1=frac{F_1}{S_1}left(1right).]
Давление второго поршня на жидкость составляет:
[p_2=frac{F_2}{S_2}left(2right).]
Если поршни находятся в равновесии то давления $p_1$ и $p_2$ равны, следовательно, мы можем приравнять правые части выражений (1) и (2):
[frac{F_1}{S_1}=frac{F_2}{S_2}left(3right).]
Определим, каким будет модуль силы, прикладываемой к первому поршню:
[F_1=F_2frac{S_1}{S_2}(4)]
Из формулы (4), видим, что величина $F_1$ больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз.
И так, применяя гидравлический пресс можно небольшой силой уравновесить гораздо большую силу. Отношение $frac{F_1}{F_2}$ показывает выигрыш в силе.
Пресс работает так. Тело, которое необходимо спрессовать, укладывают на платформу, которая лежит на большом поршне. С помощью малого поршня создают высокое давление на жидкость. Большой поршень вместе со сжимаемым телом поднимается, упирается в неподвижную платформу, находящуюся над ними, тело сжимается.
Из малого цилиндра в большой жидкость перекачивают повторным движением поршня малой площади. Делают это следующим образом. Малый поршень поднимается, открывается клапан, при этом в пространство под малым поршнем засасывается жидкость. Когда малый поршень опускается жидкость, оказывая на клапан давление, его закрывает, при этом открывается клапан, который пропускает жидкость в большой сосуд.
Примеры задач с решением
Пример 1
Задание. Каким будет выигрыш в силе у гидравлического пресса, если при действии на малый поршень (площадью $S_1=10 {см}^2$) с силой $F_1=800$ Н, получают силу, воздействия на большой поршень ($S_2=1000 {см}^2$) равной $F_2=72000 $ Н?
Какой выигрыш в силе получался бы у этого пресса, если бы отсутствовали силы трения?
Решение. Выигрышем в силе называют отношение модулей полученной силы к приложенной:
[frac{F_2}{F_1}=frac{72000}{800}=90.]
Используя формулу, полученную для гидравлического пресса:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(1.1right),]
найдем выигрыш в силе при отсутствии сил трения:
[frac{F_2}{F_1}=frac{S_2}{S_1}=frac{1000}{10}=100.]
Ответ. Выигрыш в силе в прессе при наличии сил трения равен $frac{F_2}{F_1}=90.$ Без трения он был бы равен $frac{F_2}{F_1}=100.$
Пример 2
Задание. Используя гидравлический подъемный механизм, следует поднять груз имеющий массу $m$. Какое число раз ($k$) нужно опустить малый поршень за время $t$, если за один раз он опускается на расстояние $l$? Отношение площадей поршней подъемника равно: $frac{S_1}{S_2}=frac{1}{n}$ ($n>1$). Коэффициент полезного действия машины составляет $eta $ при мощности его двигателя $N$.
Решение. Принципиальная схема работы гидравлического подъемника изображена на рис.2., она аналогична работе гидравлического пресса.
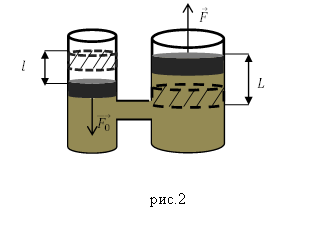
В качестве основы для решения задачи используем выражение, связывающее мощность и работу, но при этом учтем, КПД подъемника, тогда мощность равна:
[N=frac{eta A}{t}to A=eta Ntleft(2.1right).]
Работу производят с целью груз поднять, значит, ее найдем как изменение потенциальной энергии груза, за ноль потенциальной энергии будем считать энергию груза в месте начала его подъема ($E_{p1}$=0), имеем:
[A=E_{p2}-E_{p1}=E_{p2}=mgh left(2.2right),]
где $h$ – высота, на которую подняли груз. Приравняв правые части формул (2.1) и (2.2), найдем высоту, на которую подняли груз:
[eta Nt=mghto h=frac{eta Nt}{mg}left(2.3right).]
Работу, выполняемую силой $F_0$, при перемещении малого поршня найдем как:
[А_1=F_0l left(2.4right),]
Работа силы, которая двигает большой поршень вверх (сжимает гипотетическое тело), равна:
[А_2=FL .] [А_1=А_2to F_0l=FL] [frac{F_0}{F}=frac{L}{l}=frac{S_1}{S_2}left(2.5right),]
где $L$ – расстояние, на которое сдвигается большой поршень за один ход. Из (2.5) имеем:
[frac{S_1}{S_2}=frac{L}{l}to L=frac{S_1}{S_2}l left(2.6right).]
Для того чтобы найти количество ходов поршней (число раз которое опустится малый поршень или поднимется большой) следует высоту поднятия груза разделить на расстояние на которое сдвигается большой поршень за один ход:
[k=frac{h}{L}=frac{eta NtS_2}{mgS_1l}=frac{eta Ntn}{mgl}.]
Ответ. $k=frac{eta Ntn}{mgl}$
Читать дальше: закон Архимеда.
Источник
Чтобы понять принцип работы гидравлического пресса, вспомним правило сообщающихся сосудов. Его автор Блез Паскаль установил, что если они наполнены однородной жидкостью, то ее уровень во всех сосудах одинаков. При этом конфигурация емкостей и их размеры не имеют значения. В статье будут описаны несколько опытов с сообщающимися емкостями, которые помогут нам разобраться в устройстве и принципе работы гидравлического пресса.
Эксперимент
Допустим, у нас есть сообщающиеся сосуды с разной площадью поперечного сечения. Площадь меньшего обозначим s, большего – S. Наполним емкости жидкостью. По закону сообщающихся сосудов поверхности жидкостей находятся на одной высоте.
Вам будет интересно:Население Земли в 1900 году и последующий рост

Закроем сосуды сверху поршнями. Можно считать, что s и S – это площади поршней. Надавим на меньший силой f. Он пойдет вниз, жидкость будет перетекать в больший цилиндр, и поршень слева начнет подниматься. Чтобы не дать ему подниматься, мы тоже приложим к нему силу. Обозначим ее F.
Чтобы приблизиться к пониманию принципа работы гидравлического пресса, попробуем найти связь между этими двумя силами. Будем исходить из условия равновесия. До того, как мы накрыли сосуды поршнями, жидкости находились в равновесии. Давление в емкостях было одинаковым (p=P). Надавим на оба поршня так, чтобы жидкость по-прежнему оставалась в равновесии. Давления p и Р, конечно же, увеличатся. Однако они по-прежнему останутся одинаковыми, потому что увеличатся на одну и ту же дополнительную величину. Это величина давления, создаваемого поршнями. Она по закону Паскаля передается всюду.
Вот условие равновесия: p=Р. Можно рассматривать давление, создаваемое поршнями, или давление столба жидкости. Результат будет один и тот же. Заметим, что давление, создаваемое поршнями, в тысячу раз больше, чем гидростатическое давление столба жидкости. Столбик воды высотой в несколько сантиметров создает давление в сотни паскалей. А давление поршня составляет сотни килопаскалей, а иногда и мегапаскалей. Поэтому в дальнейшем мы будем пренебрегать давлением столба жидкости и считать, что давления p и Р созданы исключительно силами f и F.
Зависимость силы давления поршней от их площади
Выведем формулу, принцип работы гидравлического пресса без нее будет непонятен. p=f/s и аналогично P=F/S. Сделаем подстановку в условие равновесия. f/s=F/S. А теперь сравним силы f и F. Для этого и левую, и правую часть выражения умножим на S и разделим на f. Получим f*S/s*f=F*S/S*f. Сократим f и S в обеих частях. Результатом будет равенство F/f=S/s.
Понятие выигрыша в силе
Вам будет интересно:Сколько лет миру? Гипотезы происхождения жизни на Земле
Если S>s, то сила давления на поршень в большом сосуде будет во столько раз больше силы, которая давит на малый поршень, во сколько раз площадь более крупного поршня превышает площадь малого. Иными словами, прикладывая небольшую силу к маленькому поршню, в большом сосуде мы получим силу, намного превышающую ту, с которой мы давим на маленький поршень. Это эффект, который называется выигрыш в силе. Он показывает, во сколько раз силы отличаются, т. е. чему равно отношение F к f. Если мы возьмем сосуды, площади поперечного сечения которых сильно отличаются, то можем получить выигрыш в силе и в десять, и в тысячу раз. Анализ сил дает понять: выигрыш в силе равен отношению площадей большого и малого поршня.
Движение поршней гидравлической машины
Во многих отраслях используется принцип работы гидравлического пресса: в физике, строительстве, обработке материалов, сельском хозяйстве, автомобилестроении и т. д. Примеры применения гидравлических машин представлены на рисунке.

Рассмотрим все те же два сообщающихся сосуда с поршнями, но теперь мы будем обращать внимание не на силу, а на расстояние, которое проходят поршни при перемещении. Представим, что первоначальное их положение разное. Поршень площадью S расположен ниже поршня площадью s. Переместим меньший поршень на расстоянии h. Вода из меньшего сосуда перешла в больший и надавила на поршень. Он переместился на высоту H.

Зная соотношение между площадями, найдем соотношение между высотами. Объем, который ушел под давлением из левого цилиндра в правый, обозначим v. В правый цилиндр зашла жидкость объемом V. Жидкость несжимаема. Как это можно записать математически? v=V. Выразим объем через площадь и высоту. v=s*h и V=S*H. Значит, s*h=S*H. S/s=h/H. Следовательно, выигрыш в силе F/f=h/H. Это соотношение дает нам понимание принципа работы гидравлического пресса. Мы делаем вывод: поскольку F больше, чем f, то H меньше h, причем во столько же раз.
Допустим, гидравлическая машина дает выигрыш в силе в сто раз. Это значит, что если мы опустим меньший поршень на 100 мм, то другой поршень поднимется всего на 1 мм. А есть машины, которые дают выигрыш в силе в тысячу раз. А как же быть в случаях, когда на поршне стоит автомобиль и его нужно поднять на высоту нескольких метров?

Устройство и принцип работы гидравлического пресса
В поршне небольшой площади находится клапан, который закрывает трубочку, ведущую в резервуар с машинным маслом. Воду в гидравлических прессах обычно не используют, потому что она вызывает коррозию, к тому же у нее сравнительно низкая температура кипения. Поршень приводит в движение рукоятка. Жидкость передается из меньшего цилиндра в больший через трубочку.
В большом сосуде тоже есть клапан и поршень. Когда мы поднимаем рычаг, масло при помощи атмосферного давления всасывается в меньший цилиндр. Когда мы опускаем поршень, клапан закрывается, маслу деваться некуда, поэтому оно переходит в больший сосуд. Оно приподнимает клапан в нем, объем масла увеличивается, из-за этого поднимается поршень. Когда мы снова поднимаем малый поршень, клапан в большом сосуде закрывается, поэтому масло никуда не уходит и поршень остается на месте.

Принцип работы гидравлического пресса таков, что любые колебания малого поршня всегда приводят к движению большого поршня вверх. В устройстве предусмотрен механизм, который позволяет большому поршню опускаться. Это шланг с краном в большем сосуде. Когда мы закрываем кран, мы герметизируем большой цилиндр, а когда открываем, то приводим гидравлический пресс в исходное положение, масло сливается. Оно возвращается в резервуар, что позволяет опустить поршень.
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.

Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
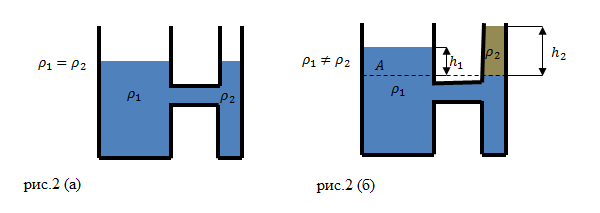
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
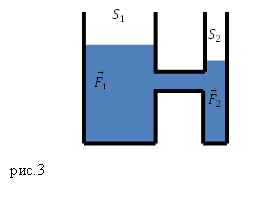
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
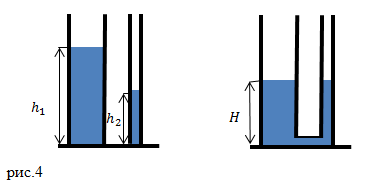
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=] [=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
В этом состоянии сохраняется объем, но не сохраняется форма. Например, если перелить молоко из кувшина в стакан – молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.
Расстояние между молекулами в жидком состоянии чуть больше, чем в твердом, но все равно невелико. При этом частицы не собраны в кристаллическую решетку, а расположены хаотично. Молекулы почти не двигаются, но при нагревании жидкости делают это более охотно.
Вспомните, что происходит, если залить чайный пакетик холодной водой – он почти не заваривается. А вот если налить кипяточку – чай точно будет готов.
Агрегатных состояния точно три?
На самом деле, есть еще четвертое – плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ – газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Сообщающиеся сосуды
Поскольку жидкость принимает форму сосуда, в который ее поместили, имеет место быть такое явление, как сообщающиеся сосуды.
- Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости (в каждом сосуде). Так жидкость может перемещаться из одного сосуда в другой.
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Если в колена сообщающихся сосудов налить жидкости, плотности которых будут различны, то меньший объём более плотной жидкости в одном колене уравновесит больший объём менее плотной жидкости в другом колене сосуда.
Другими словами, высота столба жидкости с меньшей плотностью больше, чем высота столба жидкости с большей плотностью. Давайте рассчитаем, во сколько высота столба жидкости с меньшей плотностью больше высоты столба жидкости с большей плотностью, если эти две несмешивающиеся жидкости находятся в сообщающихся сосудах.
p = ρgh, p1 = p2, ρ1 gh1= ρ2 gh2,
Отсюда:
h1/h2 = ρ1/ρ2
ρ2 = (h1/h2) * ρ1
Применение сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор состоит из двух сообщающихся сосудов: двух вертикальных стеклянных трубок, соединенных между собой третьей изогнутой трубкой.
Одна из вертикальных трубок заполняется жидкостью, плотность которой нужно определить, а другая – жидкостью известной плотности (например, водой, плотность которой равна 1000 кг/м^3). Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).
Также на законе сообщающихся сосудах основаны устройства, которые определяют уровень жидкости в закрытых сосудах: резервуарах, паровых котлах.
Чтобы судно могло переплыть из одной водного бассейна в другой, если уровни воды в них разные, необходимо использовать шлюз. Устройство шлюза также основано на принципе сообщающихся сосудов. В первых воротах шлюза открывается клапан, камера соединяется с водоёмом, они становятся сообщающимися сосудами, уровни воды в них выравниваются. После этого ворота открываются, и судно проходит в первую камеру. Открывается следующий клапан, после выравнивания уровней воды открываются ворота, и так повторяется столько раз, сколько камер имеет шлюз.
Давление столба жидкости
Выведем формулу давления столба жидкости через основную формулу давления.
Давление
p = F/S
p – давление [Па]
F – сила [Н]
S – площадь [м^2]
В случае давления жидкости на дно сосуда мы можем заменить силу в формуле на силу тяжести.
p = mg/S
Также мы можем представить массу жидкости, как произведение плотности на объем:
p = ρ*V*g/S
Из геометрии мы знаем, что объем тела вращения (например, цилиндра) – это произведение площади основания на высоту: V = Sh.
Следовательно, высота будет равна h = V/S. Подставляем в формулу высоту вместо отношения объема к площади.
p = ρ*g*V/S
p = ρgh
В сообщающихся сосудах давление жидкости на одном уровне (на одной и той же высоте) будет одинаковым.
А можно сделать так, чтобы давление было разным?
С помощью перегородки можно сделать так, чтобы уровень жидкости, а следовательно, и давления в сообщающихся сосудах отличались.
Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем дополнительное давление. Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд, где её уровень ниже – до тех пор, пока высота жидкости в обоих сосудах не станет одинаковой.
Этот принцип используют в водонапорной башне. Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.
Задачка
Какой площади необходимо сделать малый поршень в гидравлическом прессе, для того, чтобы выигрыш в силе получился равным 2? Площадь большого поршня равна 10 см^2.
Решение:
Гидравлический пресс – это два цилиндрических сообщающихся сосуда. Площадь большого поршня, с приложенной силой F1, равна 10 см^2.
Площадь малого поршня обозначим Sмал, к нему приложена сила F2.
Давления в сообщающихся сосудах на одинаковой высоте равны: p1 = p2
Подставим формулу давления:
F1/Sбол=F2/Sмал.
Выразим Sмал, получим:
Sмал = (F2/F1) * Sбол
Так как по условию выигрыш в силе F2/F1 равен 2, то:
Sмал=2*Sбол= 2*10 = 20 см^2
Ответ: малый поршень необходимо сделать с площадью равной 20 см^2
Понимать и любить этот мир гораздо проще, когда разбираешься в физике. В этом помогут небезразличные и компетентные преподаватели онлайн-школы Skysmart.
Чтобы формулы и задачки ожили и стали более дружелюбными, на уроках мы разбираем примеры из обычной жизни современных подростков. Приходите на бесплатный вводный урок по физике и начните учиться в удовольствие уже завтра!
Источник
