Масса газа в сосуде не менялась

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
(2)
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1.

Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на –диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре , второй — при температуре .

Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):

Рис. 3. Изотермы на и -диаграммах
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):

Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на –диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5):

Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):

Рис. 6. Изобары на и -диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7):

Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на –диаграмме (рис. 8):

Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):

Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Источник
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
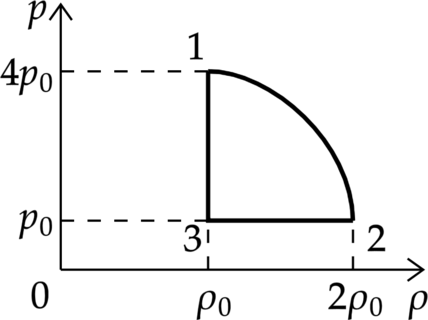
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 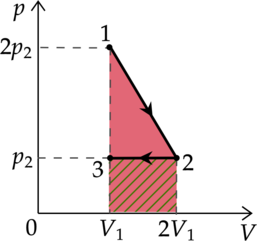
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 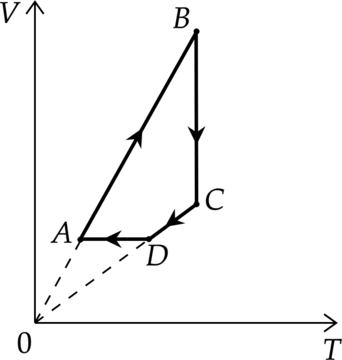
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 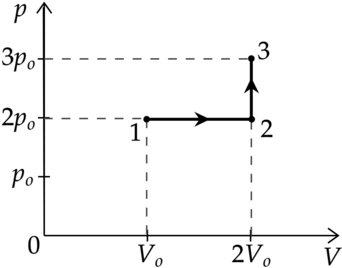
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник
