Медный шарик поместили в откачанный сосуд
Примеры решения задач по квантовой физике
1. Мощность излучения абсолютно черного тела кВт. Найти площадь излучающей поверхности тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны нм.
Дано: | Решение: |
ачт кВт нм | Энергетическая светимость тела по определению: или для тела равномерно излучающего со всей поверхности : , где − мощность излучения, − площадь излучающей поверхности. Энергетическая светимость абсолютно черного тела согласно закону Стефана-Больцмана: где Вт/(м2∙К4) − постоянная Стефана-Больцмана, − абсолютная температура абсолютно черного тела. Согласно закону смещения Вина: ; где − длина волны, на которую приходится максимум испускательной способности ачт, − температура ачт; м∙К − постоянная в законе смещения Вина. Тогда температуру тела можно выразить, как ; и, соответственно, энергетическую светимость . Следовательно, площадь излучающей поверхности тела м. |
Ответ: | м. |
2. Увеличение температуры равновесного излучения на К привело к изменению наиболее вероятной длины волны в его спектре на нм. Какова начальная температура равновесного излучения?
Дано: | Решение: |
К нм | Согласно закону смещения Вина: ; где − длина волны, на которую приходится максимум спектральной плотности излучения, т.е. наиболее вероятная длина волны в спектре излучения, − температура равновесного излучения; м∙К. Так как температура равновесного излучения увеличилась, т.е. , то длина волны уменьшилась, т.е. . Тогда . Так как , то и, следовательно, . Решим уравнение: ; ; ; ; Т.к. температура , то . . |
Ответ: | . |
3. Медный шарик радиусом мм с абсолютно черной поверхностью поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю К. Начальная температура шарика К. Через какое время его температура уменьшится в раза? Удельная теплоемкость меди Дж/(кг∙К).
Дано: | Решение: |
Шарик − ачт: ммм К Дж/(кг∙К) г/см3кг/м3 стенки сосуда: | Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности : , Энергетическая светимость абсолютно черного тела согласно закону Стефана-Больцмана: где Вт/(м2∙К4) − постоянная Стефана-Больцмана, − абсолютная температура ачт. Тогда энергия, излучаемая с поверхности шарика за время : . Т.к. шарик помещен в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю К, то шарик излучает энергию, но не поглощает. Тогда охлаждение шарика происходит при условии, что количество теплоты , теряемое шариком при охлаждении на за время , равно энергии , излучаемой с поверхности шарика за время : ; знак «-» учитывает, что , а ; − удельная теплоемкость материала шарика, − масса шарика. Тогда ; . Проинтегрируем последнее выражение: ; Получим ; . ч. |
Ответ: | ч. |
4. Какую мощность нужно подводить к зачерненному металлическому шарику диаметром см, чтобы поддерживать его температуру на К выше температуры окружающей среды? Температура окружающей среды К. Считать, что тепло теряется только вследствие излучения.
Дано: | Решение: |
Шарик − ачт: смм К К | Энергетическая светимость тела по определению: или для шарика равномерно излучающего со всей поверхности : , где − мощность излучения, − площадь поверхности шарика. Энергетическая светимость абсолютно черного тела согласно закону Стефана-Больцмана: где Вт/(м2∙К4) − постоянная Стефана-Больцмана, − абсолютная температура абсолютно черного тела. Так как шарик можно рассматривать как ачт, то: . Мощность излучения с поверхности шарика (энергия, излучаемая с поверхности шарика за единицу времени): . Так как шарик находится в среде с температурой , то поглощает излучение мощностью: . Чтобы поддерживать температуру шарика постоянной и , необходимо подводить тепловую мощность: . Вт. |
Ответ: | Вт. |
5. Определить, с какой скоростью должен двигаться и какую кинетическую энергию должен иметь электрон, чтобы его импульс был равен импульсу фотона, длина волны которого пм.
Дано: | Решение: |
МэВ кг фотон: пм | Импульс фотона: . Импульс электрона: или . 1) Так как , то ; . Решим квадратное уравнение: ; ; . Кинетическая энергия электронов , тогда: МэВДж. 2) Так как , то ; ; ; м/с. |
Ответ: | МэВДж; м/с.. |
6. Рубиновый лазер излучает в импульсе длительностью мс энергию Дж в виде узкого, почти параллельного пучка монохроматического света. Найти среднее за время импульса давление пучка света, если его сфокусировать в пятнышко диаметром мкм на поверхность, перпендикулярную пучку, с коэффициентом отражения .
Дано: | Решение: |
мсс Дж мкмм | Давление света: ; где − объемная плотность энергии излучения; − площадь светового пятна; − угол падения светового пучка на поверхность . Тогда давление Па. |
Ответ: | Па. |
7. Определить напряжение на рентгеновской трубке и скорость электронов , подлетающих к аноду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра нм.
Дано: | Решение: |
Тормозное рентгеновское излучение нм | Кинетическая энергия электронов , подлетающих к аноду рентгеновской трубки, равна: . Максимальная энергия фотона, излучаемого электроном при резком торможении на аноде рентгеновской трубки: ; . Следовательно, напряжение на рентгеновской трубке: В; кинетическая энергия электронов , подлетающих к аноду рентгеновской |
Источник
При работе с программой обратите внимание на следующее: • заголовок слайда имеет свой оттенок для каждой задачи; • указание номера задачи в формате № 5. *** отсылает нас к задачнику Иродова И. Е. 1988 года издания; • разбор задач рекомендуется проводить с ручкой и бумагой, проверяя все выкладки и расчеты; • появление в правом нижнем углу управляющей кнопки означает, что программа данного слайда выполнена и можно переходить к следующему слайду; • на слайдах с задачами для самостоятельного решения есть кнопки с подсказками, но рекомендуется пользоваться ими только в том случае, если не удается решить задачу самостоятельно; • возвращение к слайду с условием со слайда указания осуществляется при нажатии на управляющую стрелку «назад» ; • ответ на слайде с условием появляется при нажатии кнопки 1 мыши или клавиши ENTER. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Связь энергетической светимости и объёмной плотности излучения Показать, что равновесная спектральная плотность излучения u связана с энергетической светимостью R соотношением где с – скорость света.
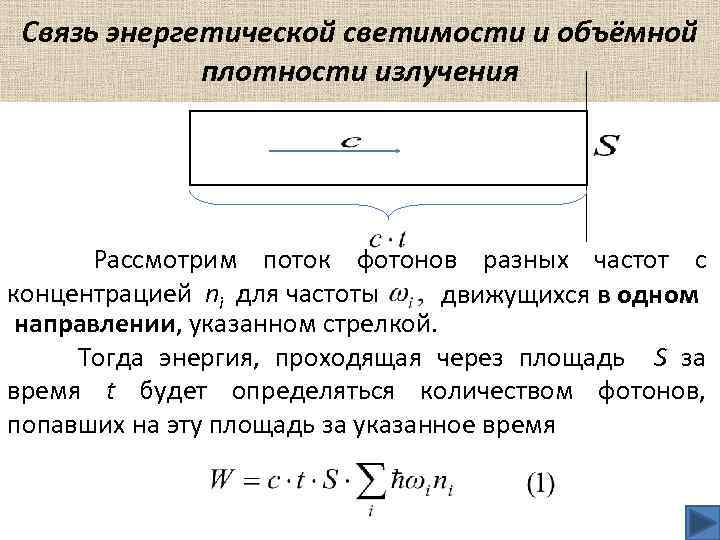Связь энергетической светимости и объёмной плотности излучения Рассмотрим поток фотонов разных частот с концентрацией ni для частоты движущихся в одном направлении, указанном стрелкой. Тогда энергия, проходящая через площадь S за время t будет определяться количеством фотонов, попавших на эту площадь за указанное время
Связь энергетической светимости и объёмной плотности излучения Каждое слагаемое представляет собой энергию всех фотонов частотой находящихся в единице объема, а сумма есть энергия всех фотонов в единице объема, то есть объемная плотность энергии u.
Связь энергетической светимости и объёмной плотности излучения На основании выражений (1) и (2) можно утверждать, что количество энергии, проходящей через площадку S за время t определяется отношением
Связь энергетической светимости и объёмной плотности излучения Рассмотрим теперь полость, заполненную равновесным излучением. Через каждую точку полости проходит бесконечное количество фотонов, направления которых равномерно распределено в пределах телесного угла Половина из них движется к рассматриваемой точке, и только половина – от неё. Поток энергии в пределах полусферы будет определяться выражением или
Связь энергетической светимости и объёмной плотности излучения Количество энергии, выходящей из площадки S, расположенной на границе полости, в единицу времени будет равно тогда Этот поток энергии должен быть таким же, какой излучают абсолютно черные стенки (условие равновесия!), то есть тогда или
№ 5. 263 Имеется два абсолютно черных источника теплового излучения. Температура одного из них найти температуру другого источника, если длина волны, отвечающая максимуму его испускательной способности, на больше длины волны, соответствующей максимуму испускательной способности первого источника.
№ 5. 263 Решение Дано: Для решения задачи используем закон смещения Вина. Запишем его для каждого источника: Выражая длину волны из первого уравнения системы подставим ее во второе уравнение:
№ 5. 263 Решение Дано: Выражая температуру, получаем: Переведем данные в систему СИ и подставим в формулу:
№ 5. 265 Излучение Солнца по своему спектральному составу близко к излучению абсолютно чёрного тела, для которого максимум испускательной способности приходится на длину волны 0, 48 мкм. Найти массу, теряемую Солнцем ежесекундно за счет этого излучения. Оценить время, в течении которого масса Солнца уменьшится на 1%.
№ 5. 265 Решение Дано: Будем решать задачу, предполагая, что за время 1 секунда масса Солнца, его температура и энергетическая светимость меняется незначительно. Аналогичное предположение сделаем для интервала времени, за которое масса Солнца уменьшится на 1% Связь между потерянной массой и испущенной энергии найдем с помощью формулы Эйнштейна:
№ 5. 265 Решение Дано: Испущенную Солнцем энергию выразим через энергетическую светимость: где – площадь поверхности Солнца Объединяя формулы (1) и (2), получаем:
№ 5. 265 Решение Дано: Выразим энергетическую светимость через длину волны, соответствующую максимуму испускательной способности, используя закон Стефана-Больцмана и закон смещения Вина: Отсюда: Подставляя полученное выражение в (3), получаем:
№ 5. 265 Решение Дано: откуда: где радиус Солнца Переведем данные в систему СИ и подставим в формулу:
№ 5. 265 Решение Дано: Для определения времени t за которое Солнце потеряет 1% своей массы, будем считать, что скорость потери массы не зависит от времени и используем результат где масса Солнца Таким образом:
№ 5. 265 Решение Дано: Переведем данные в систему СИ и подставим в формулу: Хотя ответ получен в единицах системы СИ, его имеет смысл выразить в годах, считая, что один год – это примерно Тогда Для справки: согласно данным Википедии, считается, что Солнце сформировалось примерно 4, 59 млрд лет назад
№ 5. 567 Медный шарик диаметра D=1, 2 см поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика Т 0=300 К. Считая поверхность шарика абсолютно черной, найти, через какое время его температура уменьшится в 2 раза. Построить график зависимости температуры от времени.
№ 5. 567 Решение Дано: Будем решать задачу, предполагая, что при остывании объём шара не меняется, то есть механическая работа не совершается. Значит, первый закон термодинамики можно записать так: Тогда изменение внутренней остывания запишем в виде энергии в процессе То же изменение внутренней энергии можно выразить через энергетическую светимость и площадь поверхности:
№ 5. 567 Замечание Обратим внимание на разные знаки в уравнениях (1) и (2). Первое уравнение описывает процесс остывания тела, то есть процесс уменьшения температуры. Тело отдает тепло: Второе уравнение описывает изменение внутренней энергии тела за счет теплового излучения, то есть именно то количество энергии, которое излучено телом: Первое уравнение может быть как со знаком «+» – тело нагревается, так и со знаком «-» – тело остывает, как в нашем случае. Второе уравнение всегда со знаком «+» !
№ 5. 567 Решение Дано: Приравняем левые уравнений (1) и (2): и правые части Используя закон Стефана – Больцмана, выразим связь энергетической светимости с температурой: Подставляя это выражение в (3), получаем:
№ 5. 567 Решение Дано: Разделим переменные (температуру – влево, время и константы – вправо): Заметим, что поскольку в разные моменты времени одному и тому же интервалу времени dt соответствует разное изменение температуры d. T, мы не можем перейти к конечным приращениям, а должны использовать бесконечно малые и интегрировать для нахождения зависимости T(t).
№ 5. 567 Решение Дано: Проинтегрируем выражение (3 а), учитывая, что начальному моменту времени t=0 соответствует температура Т 0, а произвольному моменту времени t температура T(t) После интегрирования получаем:
№ 5. 567 Решение Дано: Подставим пределы интегрирования: Окончательно Откуда
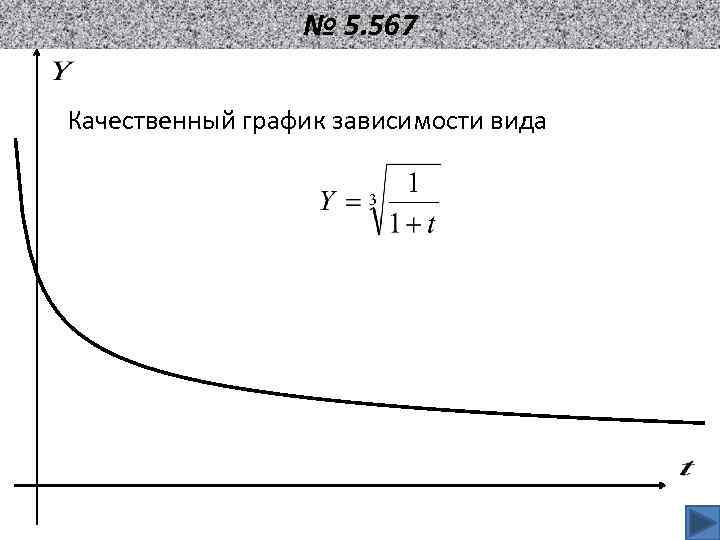№ 5. 567 Качественный график зависимости вида
№ 5. 567 Решение Дано: Вернемся к уравнению (4): и найдем время, за которое температура уменьшится в 2 раза Откуда
№ 5. 567 Решение Дано: Выразив массу m медного шарика через его объем и плотность: окончательно получаем Подставляя численные значения в единицах системы СИ, получим:
Лампа накаливания Определите длину волны, соответствующую максимуму энергии излучения лампы накаливания. Нить накала лампы имеет длину l =15 см и диаметр d=0, 03 мм. Мощность , потребляемая лампой, Р=10 Вт. Нить лампы считать абсолютно черным телом, 20% мощности которого передается другим телам вследствие теплопроводности и конвекции.
Лампа накаливания Решение Дано: По закону смещения Вина: По закону Стефана-Больцмана: Свяжем мощность излучения энергетической светимостью: где площадь поверхности нити Объединим формулы (1), (2) и (3) в систему с
Лампа накаливания Решение Дано: Выражая температуру Т из двух последних уравнений, подставим ее в первое уравнение и найдем длину волны, соответствующую максимуму испускательной способности:
Лампа накаливания Решение Дано: Переведем данные в систему СИ и поставим в формулу:
№ 5. 274 Преобразовать формулу Планка для объёмной от переменной спектральной плотности излучения (линейная частота) и к переменным (длина волны).
№ 5. 274 Решение Запишем связь между переменными Видно, что в выражении (2) взаимосвязь между переменными линейная, а в выражении (3) – нет. На основании выражений (2) и (3) найдем взаимосвязь между бесконечно малыми приращениями переменных:
№ 5. 274 Решение Знак «-» в формуле (5) указывает только на то, что частота убывает с увеличением длины волны, поэтому в дальнейшем мы его опустим и на основании уравнений (4) и (5) запишем: В дальнейшем решении примем во внимание связь между энергетической светимостью и объемной спектральной плотностью энергии: и
№ 5. 274 Решение Эти выражения можно представить производной сложной функции: и С учетом (1), (2), (3), (4 а) и (5 а) получим: в виде
№ 5. 274 Решение Дальнейшие преобразования позволяют получить окончательное выражение для формулы Планка:
Задачи для самостоятельного решения
№ С 1. 1 (5. 264) Энергетическая светимость абсолютно черного тела R=3 Вт/см 2. Определите длину волны, отвечающую максимуму испускательной способности этого тела. Указание 1 Ответ: Указание 2
№ С 1. 2 Мощность излучения абсолютно черного тела Р=105 Вт. Чему равна площадь излучающей поверхности тела, если длина волны, на которую приходится максимум излучения равна Указание 1 Ответ: Указание 2
№ С 1. 3 В следствии изменения температуры тела максимум его спектральной энергетической светимости переместился с до Тело абсолютно черное. Во сколько раз и как изменилась: а) температура тела; б) энергетическая светимость? Указание 1 Ответ: Указание 2
№ С 1. 4 (5. 275) Найти с помощью формулы Планка мощность излучения единицы поверхности абсолютно черного тела, приходящегося на узкий спектральный диапазон вблизи максимума спектральной Плотности излучения, при температуре тела Т=3000 К. Указание 1 Ответ: Указание 2
Указание 1 к № С 1. 1 Используйте закон смещения Вина и закон Стефана-Больцмана 42
Указание 2 к № С 1. 1 С помощью закона Стефана-Больцмана свяжите температуру и энергетическую светимость, с помощью закона смещения Вина – температуру и длину волны. Решите получившуюся систему из двух уравнений. 43
Указание 1 к № С 1. 2 Используйте закон смещения Вина и закон Стефана-Больцмана 44
Указание 2 к № С 1. 2 С помощью закона Стефана-Больцмана свяжите температуру и энергетическую светимость, с помощью закона смещения Вина – температуру и длину волны. Свяжите энергетическую светимость с мощностью излучения. Решите получившуюся систему из трех уравнений. 45
Указание 1 к № С 1. 3 Используйте закон смещения Вина и закон Стефана-Больцмана 46
Указание 2 к № С 1. 3 Если Указания 1 оказалось недостаточно, то попробуйте: • обратиться к друзьям; • прийти на консультацию; • сменить институт . 47
Указание 1 к № С 1. 4 Учтите связь между спектральной плотностью энергии и испускательной способностью 48
Указание 2 к № С 1. 4 Используйте закон смещения Вина и учтите, что в узком спектральном диапазоне при интегрировании по длине волны спектральная испускательная способность практически постоянна 49
Источник
В категории материалов
: 787
Показано материалов
: 321-330
Маховое колесо, имеющее момент инерции 245 кг×м2, вращается, делая 25 об/с. Через 1 минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Определить: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Маховое колесо, имеющее момент инерции 245 кг×м2, вращается, делая 20 об/с. Через 1 минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Определить: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Маятник состоит из очень легкого стержня, на которомзакреплены два одинаковых груза малых размеров: один на расстоянии 30 см от оси, другой нарасстоянии 15 смот оси. Найти период колебаний маятника.
Медный шарик диаметра d = 1,2 см поместили в откачанный сосуд, температура которого поддерживается близкой к абсолютному нулю. Начальная температура шарика Т0 = 300 К. Считая поверхность шарика абсолютно чёрной, найти, через сколько времени его температура уменьшится в 2 раза. Удельная теплоёмкость меди с = 390 Дж/(кг К), плотность меди 8,9×10^3 кг/м3.
Между двумя металлическими пластинами, находящимися на расстоянии d = 6 см друг от друга создана разность потенциалов 200 В. Затем в пространство между пластинами вводится стеклянная пластинка, относительная диэлектрическая проницаемость которой равна 7, а толщина равна d. Найти поверхностную плотность р связанных зарядов, возникших на поверхности пластинки.
Между металлическими пластинами, находящимися на расстоянии d = 1 см друг от друга, создана разность потенциалов 200 В. Затем в пространство между пластинами помещают две плоскопараллельные пластинки: одну из стекла (e1 = 6, d1 = d/2), вторую из парафина (e2 = 2, d2 = d/2). Найти напряжённости поля Е1 и Е2 в каждом диэлектрическом слое, поверхностную плотность 0 свободных зарядов на металличе-ских пластинах и поверхностные плотности р1 и р2 поляризационных зарядов на ди-электрических слоях.
Между обкладками плоского конденсатора находится диэлектрик, удельное сопротивление которого изменяется по линейному закону от 1×10^11 Ом*м до 1×10^10 Ом*м. Найти ток утечки через конденсатор, если разность потенциалов между обкладками U=200 В. Площадь обкладок S=200 см2 и расстояние между ними d=3 мм.
Между обкладками плоского конденсатора, находящимися на расстоянии d = 1 см друг от друга, поддерживается постоянная разность потенциалов 2 кВ. Конденсатор заполняют диэлектриком, восприимчивость которого 1.005. Найти поверхностную плотность связанных зарядов на диэлектрике.
Между обкладками сферического конденсатора, радиусы которых r1 и r2, поддерживается постоянная разность потенциалов U. Пространство между обкладками заполнено однородной средой с удельной проводимостью s. Вычислить сопротивление между обкладками, силу тока и мощность тепловых потерь.
Между обкладками цилиндрического конденсатора с радиусами r1=3 мм и r2=6 мм поддерживается разность потенциалов U=200 В. Пространство между обкладками заполнено однородной средой с удельным сопротивле-нием 1×10^8 Ом м. Найти силу тока через конденсатор, если высота ци-линдров l=6 см.
Источник