Механизм давления газа на стенки сосуда
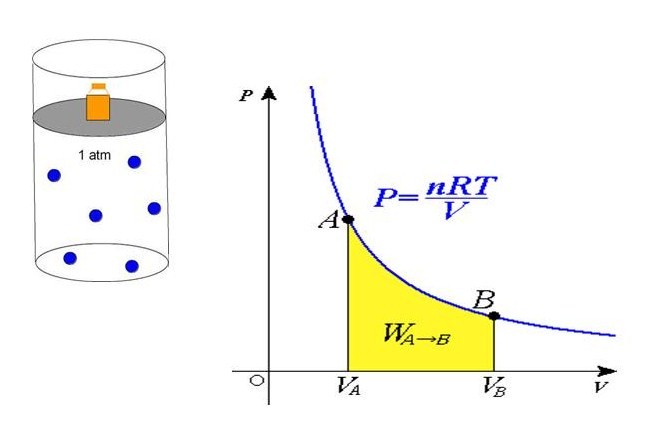
Как объясняют давление газа на основе учения о движении молекул?
Давление газа на стенки сосудов вызывается ударами молекул газа.
У газов нет ни формы ни постоянного объема. Они могут заполнить любой объем.
Количество молекул в каждом кубическом сантиметре увеличивается при сжатии (уменьшается при расширении) от этого число ударов о стенки сосуда увеличивается (уменьшается). Поэтому чем больший сосуд газ заполняет, тем меньше давление и наоборот.
Газ одинаково давит по всем направлениям, как пример -когда надуваешь воздушный шар, то он надувается равномерно.
Если газ находиться в маленьком объеме, то давление на стенки становится огромным, поэтому газ удобнее и безопаснее заключать в специальные прочные стальные баллоны.
Давление газа вызывается ударами молекул о стенки сосуда, т.к. молекулы хаотически движутся и постоянно соударяются друг с другом и со всеми встреченным препятствиями.
По Эйнштейну, чем ближе тело или частица к скорости света, тем огромнее становится его масса. И вот,в Большом адронном коллайдере, протоны и ионы, движутся почти со скоростью света, и что это значит?
Релятивистской массы нет в природе и, согласно релятивистской механике Эйнштейна, масса остаётся инвариантной и равной массе покоя всегда, независимо от скорости (недоверчивым сюда).
Темп роста энергии частицы (E) с ростом скорости β = v/c (в единицах скорости света c) получен мною здесь. Если тело обладало скоростью β₁ = 0,9 при энергии Е₁, то для достижения скорости β₂ = 0,9. 999 (n девятoк после запятой), потребуется энергия E₂ = (3,16)ⁿ⁻¹⋅Е₁. Получается, что с каждой новой девяткой в величине скорости (β), энергия должна быть увеличена в 3,16 раз. Таким образом, неограниченный рост числа девяток (n) в численном значении скорости (β), приводит к неограниченному росту энергии.
Mаксимальная скорость зарегистрированного материального объекта (протона), ускоренного до околосветовых скоростей в космическом пространстве, равна β = 0,9. 999 (всего 23 девятки), а соответствующая энергия, E
10¹¹ ГэВ. Области в галактиках и механизмы ускорения до этих скоростей пока неизвестны. Максимальные энергии столкновения протонов, достигнутые на ускорителе БАК (LHC) в ЦЕРН, равны 1,3×10⁴ ГэВ, что в системе отсчёта неподвижной мишени соответствует энергии протона = 9×10⁷ ГэВ или скорости протона β = 0,999 999 999 999 9999 (16 девяток). В обоих случаях масса протона остаётся неизменной и равной массе покоя, 0.938 ГэВ.
Согласно релятивистской механике, со скоростью света (β = 1) могут лететь только безмассовые частицы (фотоны), но и у них есть недостаток − они не могут лететь медленнее.
Источник
Основное уравнение молекулярно-кинетической теории
Урок 26. Физика 10 класс ФГОС
Конспект урока «Основное уравнение молекулярно-кинетической теории»
Самым простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ и начинают с газов. Интересно, что впервые термин «газ» (а «газ» в переводе с греческого означает ‘хаос’) был введён лишь в начале XVII века нидерландским химиком Яном Баптистом ван Гельмонтом.
На прошлом уроке мы с вами говорили о том, что молекулы газа находятся на значительном расстоянии друг от друга и способны к неограниченному расширению. Даже при редких (в масштабах молекул) столкновениях сил притяжения не хватает, чтобы удержать молекулы друг возле друга. Сталкиваясь, они разлетаются в разные стороны, подобно бильярдным шарам. Всё это приводит к тому, что средняя кинетическая энергия теплового движения молекул газа намного больше средней потенциальной энергии их взаимодействия. Поэтому часто значением последней мы пренебрегаем. Это даёт нам право воспользоваться моделью идеального газа.
Итак, идеальный газ — это модель газа, удовлетворяющая следующим условиям: молекулы газа можно считать материальными точками, которые хаотически движутся; силы взаимодействия между молекулами идеального газа практически отсутствуют (они действуют только при столкновении молекул); при столкновениях молекулы идеального газа ведут себя как абсолютно упругие шарики.
При изучении механики мы с вами вводили понятие «механической системы тел» и говорили о том, что состояние любой механической системы определяется её параметрами — координатами, скоростями и импульсами.
В тепловых процессах основными физическими величинами, характеризующими некоторое количество идеального газа как макроскопическую систему, являются давление, объём и абсолютная температура. Эти физические величины называют макроскопическими параметрами состояния газа.
А к микроскопическим параметрам состояния газа относят индивидуальные характеристики молекул: массу отдельной молекулы, её скорость, импульс и кинетическую энергию теплового движения.
Одна из важнейших задач молекулярно-кинетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами. Найдём эту связь. Для этого предположим, что у нас есть закрытый сосуд в форме куба, в котором находится идеальный одноатомный газ, находящийся в термодинамическом равновесии (так принято называть состояние, в котором все макроскопические параметры газа остаются неизменными во времени по всему объёму). Ещё в седьмом классе мы говорили о том, что газ, находящийся в сосуде, будет оказывать давление на его стенки. С точки зрения молекулярно-кинетической теории это давление вызвано ударом молекул газа о стенки сосуда. Очень слабые силы ударов отдельных молекул складываются для громадного количества молекул в значительную по величине и почти постоянную силу, действующую на тело. Усреднённое по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа.
Итак, пусть молекула идеального газа массой т движется перпендикулярно стенке куба с некоторой постоянной скоростью. В результате абсолютно упругого удара со стенкой сосуда молекула газа передаст участку стенки определённый импульс, а направление скорости молекулы измениться на противоположное. Тогда проекция изменения её импульса будет равна разности проекций импульсов до и после взаимодействия:
Для определения давления на стенку куба необходимо вычислить совокупное воздействие молекул на неё за некоторый промежуток времени.
Для этого необходимо умножить изменение импульса одной молекулы на полное число молекул, ударяющихся о стенку за данный промежуток времени:
Теперь предположим, что в кубе хаотично движется N молекул. Так как газ у нас находится в термодинамическом равновесии, то из-за беспорядочного движения молекул результат их удара о стенки таков, как если бы треть всех молекул двигалась прямолинейно между правой и левой стенкой, треть — между передней и задней стенкой и треть — между верхней стенкой и нижней. А так как все направления в пространстве равноправны, то число молекул, летящих к выбранной грани куба, составляет шестую часть всех молекул, заключённых в сосуде:
Выберем промежуток времени таким образом, чтобы все молекулы, находящиеся в сосуде, успели хотя бы раз столкнуться с одной из граней куба. При этом время полёта молекулы от одной грани до другой будет определяться отношением длины ребра куба к скорости молекулы:
Тогда суммарное изменение импульса молекул за счёт столкновения с выбранной гранью за время ∆t будет определяться выражением, которое вы видите на экране:
С другой стороны, мы с вами знаем, что изменение импульса молекул может быть определено и на основании второго закона Ньютона, записанного в импульсной форме:
Здесь
— это средняя сила реакции, действующая со стороны грани сосуда на молекулы. Она, по третьему закону Ньютона, равна по модулю силе, с которой поток молекул воздействовал на стенку. Теперь вспомним, что по определению давление газа — это средняя сила воздействия его молекул, отнесённая к единице площади:
Значение средней силы мы выразим из второго закона Ньютона:
А время полёта молекулы от одной грани до другой мы с вами нашли ранее. Давайте подставим выражения для промежутка времени и средней силы в формулу давления:
Теперь вспомним, что произведение площади грани на её ребро — это есть объём куба (в нашем случае это объём сосуда, в котором находится газ). А число молекул газа в единице объёма — это концентрация молекул.
Таким образом, мы с вами нашли давление газа для идеального случая. В реальных же условиях молекулы движутся не только хаотически, но и имеют различные скорости, что не было нами учтено. Однако, как показали расчёты, среднее значение модуля этих скоростей имеет вполне определённое значение:
То же самое будет относиться и к среднему значению квадрата скорости молекул:
Перепишем формулу для давления газа с учётом этой поправки:
Полученное нами уравнение носит название основного уравнения молекулярно-кинетической теории газов. Оно связывает макроскопическую величину — давление, которое может быть непосредственно измерено с микроскопическими параметрами молекул: массой и скоростью их хаотичного движения.
А теперь давайте проделаем такую операцию: умножим и разделим на 2 правую часть основного уравнения МКТ
И поменяем местами сомножители:
Множитель
— это средняя кинетическая энергия поступательного движения молекул.
Тогда можно записать, что давление идеального газа равно двум третям средней кинетической энергии поступательного движения всех молекул, заключённых в единице объёма:
Это уравнение тоже можно назвать основным уравнением молекулярно-кинетической теории. Но связывает оно уже другие параметры: макропараметр давление со средней кинетической энергией их поступательного движения, являющейся с микроскопической характеристикой.
Эта формула впервые была получена немецким физиком Рудольфом Клаузиусом, и поэтому её часто называют уравнением Клаузиуса.
Для примера решим с вами задачу. Кислород находится под давлением 95 кПа и имеет плотность 2,1 кг/м 3 . Определите среднюю кинетическую энергию поступательного движения его молекул.
Источник
Давление газа — формула. Формула давления газа в сосуде
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Источник
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
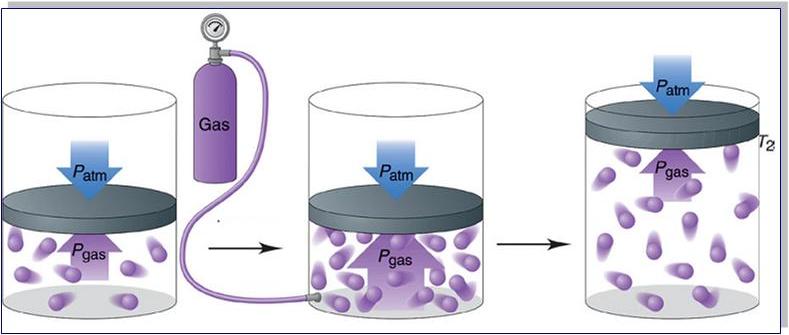
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
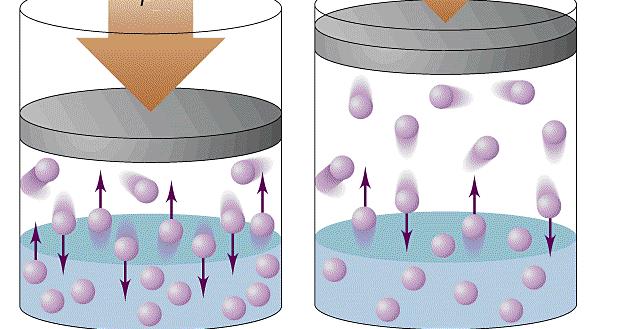
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.

Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
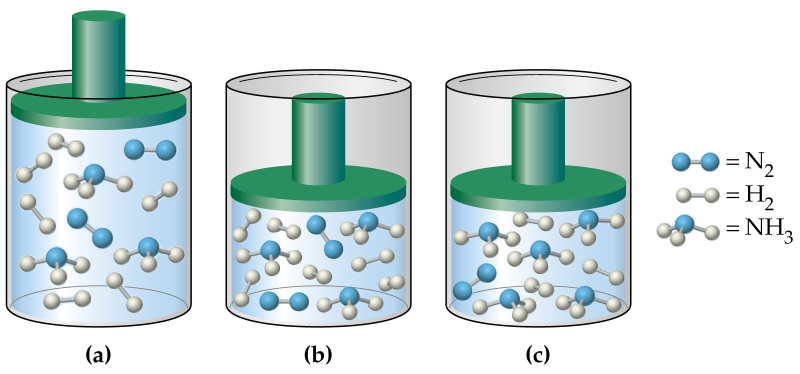
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
