Модель движения крови по сосудам
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Доль А.В.
1
Гуляев Ю.П.
1
Иванов Д.В.
1
1 ФБГОУ ВПО «Саратовский государственный университет имени Н.Г. Чернышевского»
В работе рассматриваются новые подходы к моделированию гемодинамики крупных кровеносных сосудов, которые позволяют сократить число основополагающих гипотез. Предложен алгоритм решения основной замкнутой системы уравнений динамики кровотока, а также приведены результаты расчетов начальных точек дисперсионных кривых для дисперсионного уравнения, полученного в процессе решения данной системы.
математическое моделирование
артерия
упругие стенки
осесимметричное движение крови
1. Моделирование виллизиевого круга человека в норме и при патологии / Д.В. Иванов, А.В. Доль, О.Е. Павлова, А.В. Аристамбекова // Российский журнал биомеханики. 2013. Т. 17. № 3(61). С. 36-49.
2. Педли Т. Гидродинамика крупных кровеносных сосудов / Т. Педли. М.: Мир, 1983. 400 с.
3. Смертность от болезней системы кровообращения в России и экономически развитых странах / В.И. Харченко, Е.П. Какорина, М.В. Корякин и др. // Российский кардиологический журнал. 2005. № 2. С. 5-18.
4. Berger S.A., Jou L.D. Flows in Stenotic Vessels // Annu Rev Fluid Mechanics. 2000. Vol. 32. P. 347-384.
5. Bruin A. Numerical Simulation of blood flow through elastic vessels // Master Thesis, Department of Mathematics University of Groningen. 2003. 24 p.
6. Chen J., Lu X.-Y. Numerical Investigation of the non-Newtonian Pulsatile Blood Flow in a Bifurcation Model With a Non-Planar Branch // Journal of Biomechanics. 2006. Vol. 39. P. 818-832.
7. Tambasco M., Steinman D.A. Path-Dependent Hemodynamics of the Stenosed Carotid Bifurcation // Annals of Biomedical Engineering. 2003. Vol. 31. P. 1054-1065.
8. Numerical issues of modelling blood flow in networks of vessels with pathologies / S. Simakov, V. Salamatova, Yu. Ivanov, T. Dobroserdova // Russian Journal of Numerical Analysis and Mathematical modeling. 2011. Vol. 26. Iss. 6. P. 1-18.
Введение
По статистике, сердечно-сосудистые заболевания являются одной из основных причин инвалидности и смерти жителей большинства современных развитых стран [3]. На долю смертности от заболеваний сердечно-сосудистой системы в общем приходится до 60% от общего числа умерших.
Нередко для восстановления кровообращения в пораженных сосудах помимо медикаментозного лечения проводятся реконструктивные операции, и часто невозможно объективно оценить, какой тип оперативного вмешательства будет оптимальным для конкретного пациента, а также насколько близок будет кровоток в сосуде к нормальному после операции. Основная проблема при выполнении таких расчетов состоит в определении механических свойств стенок сосудов, параметров кровотока и др.
Еще одной важной проблемой при прогнозировании результатов лечения является скорость расчетов: как правило, большинство современных математических моделей требуют численного решения, причем во многих случаях вычисления получаются затратными по времени и требуют довольно мощные компьютеры [8]. При этом снижение времени расчетов путем упрощений может привести к неточности полученных результатов, что, безусловно, недопустимо [5].
Часто для численных расчетов применяют метод конечных элементов. Однако решение задач гемодинамики с помощью МКЭ требует больших затрат по времени [5].
Таким образом, актуальной является задача построения математической модели гемодинамики, которая бы достаточно полно описывала движение крови в кровеносных сосудах, учитывая взаимодействие жидкости со стенкой, и являлась легко адаптируемой под конкретного пациента.
Материалы и методы
Рассмотрим осесимметричное движение крови, которая принимается вязкой несжимаемой жидкостью, в круглом сосуде постоянного радиуса R. Движение происходит в цилиндрической системе координат (x, r, θ), причем ось x совпадает с осью симметрии потока [2]. Материал стенки считаем идеально упругим, изотропным.
Основная система уравнений динамики кровотока в гибких цилиндрических сосудах в таком случае будет иметь вид:
, (1)
, (2)
, (3)
, (4)
, (5)
, (6)
, (7)
, ,
где p – давление; ρ – плотность крови; μ – вязкость крови; vx – осевая компонента скорости крови; vr – радиальная компонента скорости крови; R – радиус сосуда; t – время; u, w – перемещения стенки в продольном и поперечном направлениях; Sʹ, Tʹ – силы натяжения в окружном и продольном направлениях соответственно; S0, T0 – начальные значения сил натяжения в окружном и продольном направлениях; E – модуль Юнга стенки; ν – коэффициент Пуассона; h – толщина стенки сосуда; ρ0 – массовая плотность материала стенки сосуда.
На стенке записываем условия кинематического контакта стенки сосуда с жидкостью:
(8)
В случае моделирования гемодинамики крупных кровеносных сосудов в большинстве современных работ кровь полагается ньютоновской жидкостью [4, 7]. При этом в [6] показано, что разница значений (в случае крупных кровеносных сосудов), которые получаются для ньютоновской и неньютоновской жидкостей, не превышает 10%.
Уравнения (4)-(7) позволяют учесть податливость сосудистой стенки, а контактные условия (8) позволяют учесть взаимодействие стенки с потоком.
Такой подход к моделированию гемодинамики широко известен, однако основная система уравнений в этом случае не позволяет учесть конвективную составляющую ускорения частиц жидкости, а это, в свою очередь, для сосудистого русла с несколькими узлами бифуркации может оказать существенное влияние на результаты расчетов.
Основная система уравнений динамики вязкой несжимаемой жидкости в кровеносных сосудах с гибкими стенками в трехмерной постановке может быть записана в виде уравнений для направленных потоков.
Будем, как и раньше, полагать, что задача осесимметрична, а кровь является ньютоновской жидкостью.
Для направленных потоков жидкости в тонких трубках с упругими стенками на основе известного способа линеаризации возможен учет конвективного ускорения частиц жидкости в рамках линейной теории. В случае осесимметричных направленных потоков уравнения Навье-Стокса имеют следующий вид:
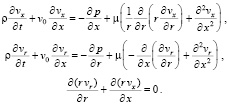 (9)
(9)
Здесь v0 – основная скорость направленного потока, вокруг которой происходит малая пульсация составляющих скоростей: vx = v0 + vʹ; vr = vʹ.
Динамические уравнения осесимметричных колебаний предварительно натянутой круглой цилиндрической оболочки записываются в виде:
(10)
где .
Условия «прилипания» частиц жидкости к стенкам сосуда заменим условием стесненного их скольжения по поверхности контакта:
(11)
λ – коэффициент вязкого трения материала оболочки и жидкости.
Рассмотрим систему уравнений (9), (10) с контактными условиями (11). Умножим уравнение (1) на r и продифференцируем по x. Далее второе уравнение системы также умножим на r и продифференцируем по r, после чего сложим левые и правые части полученных уравнений. В результате получим уравнение для давления:
. (12)
Запишем преобразованную систему уравнений:
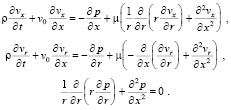 (13)
(13)
Для дальнейшего упрощения предложенной системы уравнений в трехмерной постановке можно вместо уравнений Навье-Стокса (9) использовать уравнения Эйлера для описания движения направленного потока идеальной несжимаемой жидкости, полагая при этом, что вязкое стесненное трение жидкости о стенку сосуда будет происходить в бесконечно тонком слое (погранслой) на контактной поверхности.
(14)
Вязкие свойства жидкости в погранслое будут описываться упрощенным одномерным уравнением, записанным на основании первого уравнения Навье-Стокса:
. (15)
При этом на границе погранслоя функция давления может испытывать конечный скачок. Касательные напряжения на стенке будут иметь вид:
(16)
Тогда уравнения движения оболочки примут вид:
(17)
В качестве контактных условий для идеальной жидкости можно взять условия непроницаемости стенки и условия прилипания частиц жидкости вдоль стенки:
. (18)
Из системы уравнений (14)-(17) путем простых преобразований может быть получено уравнение для давления в виде (12).
Запишем преобразованную систему уравнений:
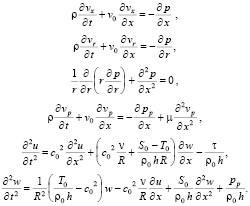 (19)
(19)
Система (19) с контактными условиями (18) представляет собой упрощенный вариант системы уравнений динамики кровотока в сосудах с упругими стенками, так как уравнения Навье-Стокса здесь заменяются уравнениями Эйлера для идеальной жидкости, которые имеют более простой вид.
Решение основной системы уравнений для случая пульсирующего кровотока как для системы (9)-(10), так и для системы (19) можно искать в виде простых гармонических волн:
, (20)
, (21)
где ω – частота пульсации кровотока, χ – волновое число.
Подставляя выражения (21) в уравнения движения жидкости основной системы, получим базовые решения для амплитуд компонент скорости и давления. В этом случае сумма базовых решений для каждой волновой гармоники даст общее решение основной системы.
Неизвестные константы необходимо определять из контактных условий, уравнений движения стенки, а также из граничных условий на входе и выходах из сосудистой системы. Это напрямую связано с решением дисперсионных уравнений, возникающих при подстановке выражений (20) в основную систему.
Были получены начальные точки (рис. 1 и 2) дисперсионных кривых для дисперсионного уравнения, полученного при решении системы (1)-(7). На рисунках значения по осям а и b – это действительная и мнимая части волнового числа.
Используя полученные точки в качестве начальных приближений для построения решения дисперсионного уравнения, можно построить необходимые дисперсионные кривые, что позволит завершить решение полной краевой задачи с учетом краевых и контактных условий и найти необходимое число констант интегрирования.
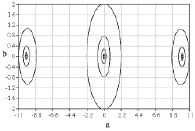
Рис. 1. Начальные точки дисперсионных кривых в случае малой вязкости
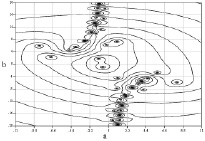
Рис. 2. Начальные точки дисперсионных кривых в случае большой вязкости
Такой алгоритм поиска общего решения системы (1)-(7) вполне подходит для решения систем (9)-(10) и (19). Таким образом, предложенные математические модели могут использоваться для исследования кровотока в системе кровеносных сосудов.
Результаты и обсуждение
Предложенные варианты постановки задач гемодинамики в системе кровеносных сосудов позволяют уменьшить количество основополагающих предположений и упростить основную систему уравнений. В случае, когда проводится учет направленных потоков жидкости, отпадает необходимость пренебрежения конвективной составляющей ускорения частиц, что повышает точность результатов.
Новый вид кинематических контактных условий стесненного скольжения (11), по мнению авторов, более адекватно описывает процесс взаимодействия потока со стенкой. В реальном сосуде в случае выполнения условий прилипания частиц неизбежным был бы процесс образования атеросклеротических отложений, который является патологическим. Таким образом, математические модели, в которых взаимодействие крови со стенкой описывается подобным образом, не могут достоверно описывать процесс гемодинамики.
Замена уравнений Навье-Стокса уравнениями Эйлера в системе (19) существенно упрощает основную систему, при этом уравнение для тонкого погранслоя вблизи стенки сосуда (15) позволяет учесть все возникающие в этой области процессы.
Таким образом, предложен ряд упрощений и уточнений, позволяющий более точно и адекватно моделировать движение крови в системе кровеносных сосудов человека.
Выводы
Предложены новые варианты постановки задач о движении крови в сосудах с упругими стенками, позволяющие уменьшить количество основополагающих гипотез и, тем самым, повысить строгость и реалистичность предлагаемых математических моделей.
Кроме того, предложен новый вид кинематических контактных условий, позволяющих более точно описать процесс взаимодействия потока крови с сосудистой стенкой.
Библиографическая ссылка
Доль А.В., Гуляев Ю.П., Иванов Д.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ КРОВИ В СИСТЕМЕ СОСУДОВ С УПРУГИМИ СТЕНКАМИ // Успехи современного естествознания. – 2014. – № 9-1. – С. 79-84;
URL: https://natural-sciences.ru/ru/article/view?id=34193 (дата обращения: 05.01.2021).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Источник
ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ г. СЕМЕЙ
Методическое пособие по теме:
Физические основы гемодинамики.
Закономерности движения крови в артериальном и венозном русле.
Составитель: Преподаватель
Ковалева Л.В.
Основные вопросы темы:
1.Понятие гемодинамики.
2. Физическая модель сосудистой системы. Работа сердца.
3. Физические основы клинического метода измерения давления крови.
4. Движение крови по сосудам. Непрерывность кровотока.
5. Систолическое и диастолическое давление, пульсовое давление крови.
6. Систолический и минутный объем кровотока.
7. Биофизические особенности аорты. Распространение пульсовой волны по стенке
артерий. Венный пульс.
8. Биофизические особенности артериол большого круга кровообращения.
Гемодинамика.
Гемодинамика один из разделов биомеханики, изучающий законы движения крови по кровеносным сосудам. Задача гемодинамики – установить взаимосвязь между основными гемодинамическими показателями, а также их зависимость от физических параметров крови и кровеносных сосудов. К основным гемодинамическим показателям относятся давление и скорость кровотока. Давление – это сила, действующая со стороны крови на сосуды, приходящаяся на единицу площади. Различаю объемную и линейную скорость кровотока. Объемной скоростью кровотока Q называют величину, численно равную объему жидкости, протекающему в единицу времени через данное сечение трубы : Q=V/t
Линейная скорость представляет путь, проходимый частицами крови в единицу времени : v=l/t. Поскольку скорость крови неодинакова по сечению сосудов, то речь пойдет о средней скорости. Линейная и объемная скорости связаны простым соотношением Q=vS, где S площадь поперечного сечения потока жидкости.
Для сплошного течения несжимаемой жидкости выполняется условие неразрывности струи: через любое сечение струи в единицу времени протекают одинаковые объемы жидкости: Q=vS=const. Для гемодинамики этот закон можно сформулировать так: в любом сечении сердечно-сосудистой системы объемная скорость кровотока одинакова.
Физическая модель сосудистой системы. Работа сердца.
Физическую модель сердечно-сосудистой системы можно представить в виде замкнутой (не имеющей сообщения сатмосферой), многократно разветвленной и заполненной жидкостью системы трубок с эластичными стенками, движение жидкости в которой происходит под действием ритмически работающего нагнетательного насоса (на рис. в виде резиновой груши). При сжатии груши содержащийся в ней объем жидкости проталкивается через отверстие клапана К1в систему трубок состороны Л,вызывая в них продвижение жидкости в сторону Б, затем клапан К1запирается, груша расширяется и через клапан К2в нее поступает соответствующий объем жидкости со стороны Б системы.
Особенностьюданной системы является, прежде всего, постепенное и множественное разветвление трубок, особенно в ее средней части. Последняя состоит из весьма большого числа коротких параллельных трубок малого сечения, общий просвет которых имеет настолько большое сечение, что скорость жидкости здесь снижается почти до нуля. Однако внутреннее трение в пристеночных слоях этих трубок настолько велико, что именноэта средняя часть системы представляет наибольшее сопротивление течению жидкости и обусловливает максимальное падение давления.
Другой особенностью системы является эластичность стенок трубок, благодаря которой при ритмической работе насоса ток жидкости в ней принимает равномерный характер. Допустим, что при сжатии груши некоторое количество жидкости поступает в трубку А, уже заполненную жидкостью под некоторым давлением. Давление в трубке А повышается,эластичные стенки ее растягиваются и вмещают избыток жидкости. Затем стенки трубки А постепенно сокращаются и прогоняют избыток жидкости в следующее звено системы, стенки которого также сначала растягиваются затем сокращаются и таким образом проталкивают жидкость в последующие звенья системы трубок. В результате течение жидкости постепенно принимает равномерный характер. Иллюстрацией подобного явления может служить следующий опыт. Две трубки {Б — жесткая и А — с эластичными стенками) с помощью тройника Т присоединены к насосу-груше Г {В — резервуар с водой). На конце трубок имеются пробки Я с небольшими отверстиями, препятствующие свободному вытеканию воды. При работе грушей можно наблюдать, как из трубы Б вытекает прерывистая струя, а из трубы А, стенки которой при этом периодически растягиваются и сокращаются — непрерывная.
Переходим к сосудистой системе. Начальное давление, необходимое для продвижения крови по всей сосудистой системе, создается работой сердца.
Рассмотрим схематически явления, происходящие в большом круге кровообращения. При каждом сокращении левого желудочка сердца в аорту, уже заполненную кровью под соответствующим давлением, выталкивается так называемый ударный объем крови, в среднем разный 65—70 мл. Затем клапаны аорты закрываются.
Поступивший в аорту дополнительный объем крови повышает давление в ней и соответственно растягивает ее стенки. Волна повышенного давления, которое называется систолическим, вызывает колебания сосудистых стенок, распространяющиеся вдоль более крупных артерий в виде упругой волны. Эта волна давления называется пульсовой волной,скорость ее распространения зависит от упругости сосудистых стенок и имеет порядок 6—8 м/с.
Затем в, период расслабления сердечной мышцы (диастола, давление крови в этот момент называется диастолическим) стенки аорты постепенно, сокращаются до исходного положения и проталкивают поступивший объем крови в более отдаленные крупные артерии. Стенки последних в свою очередь растягиваются и затем, сокращаясь, проталкивают кровьв последующие звенья сосудистой системы. В результате ток крови принимает непрерывный характер со скоростью в крупных сосудах порядка.0,3—0,5 м/с.
При таком механизме продвижения крови только часть энергии, развеваемой сердечной мышцей при сокращении, передается непосредственно массе крови в аорте и переходит в ее кинетическую энергию. Остальная часть энергии переходит в потенциальную энергию деформации растяжения эластичных стенок крупных сосудов (преимущественно аорты) и затем уже постепенно по мере возвращения их в исходное положение передается массе крови в период расслабления сердечной мышцы. Существует также такое понятие как пульсовое давление крови, равное разности систолического и диастолического давления, составляющее в большом круге кровообращения примерно 40 мм рт. ст.
Количество Q крови, протекающее через поперечное сечение участка сосудистой системы в единицу времени и называемое объемной скоростью кровотока, зависит от разности давлений в начале и конце участка и его сопротивления току крови. При расчетах объемной скорости на отдельных участках сосудистой системы в первом приближении пользуются формулой Гагена — Пуазейля, хотя сопротивление току крови в сосудистой системе выше, чем следует по формуле, вследствие потерь энергии при деформации ее эластичных стенок, а также неизбежных завихрений в местах разветвления. Точный расчет с учетом этих условий весьма сложен.
Сопротивление току крови, следовательно, и падение давления на различных участках сосудистой системы весьма различны. Оно зависит от общего просвета и числа сосудов в разветвлении. Наибольшее падение давления крови — не менее 50% от начального давления — происходит в артериолах. Число артериол в сотни раз больше числа крупных артерий при сравнительно небольшом увеличении общего просвета сосудов. Поэтому потери давления от пристеночного трения в них весьма велики. Общее число капилляров еще больше, однако длина их настолько мала, что падение давления крови в них хотя и существенно, но меньше, чем в артериолах.
В сети венозных сосудов, площадь сечения которых в среднем в два раза больше площади сечения соответствующих артерий, скорость течения крови невысока и падения давления незначительны. В крупных венах около сердца давление становится на несколько миллиметров ртутного столба ниже атмосферного. Кровь в этих условиях движется под влиянием присасывающего действия грудной клетки при вдохе.
На рис. схематически показано распределение давления крови в отдельных частях системы сосудов большого круга кровообращения. На рис. приведены графики изменения давления и скорости движения крови в основных частях сосудистой системы. Движение крови по сосудам, особенно распределение ее между различными частями самой сосудистой системы, зависит не только от работы сердца, но и от общего просвета сосудов, обусловленного тонусом сосудистых стенок. В эластичных стенках сосуда имеются гладкие мышечные волокна, от степени сокращения которых зависит просвет сосуда. Имеют значение также общее количество циркулирующей крови, ее вязкость и т. п. Все эти факторы находятся под регулирующим влиянием центральной нервной системы. Таким образом, физиологические факторы, накладываясь на физические закономерности, регулируют кровообращение в различных частях организма.
В норме сосудистая система замкнута и не имеет сообщения с атмосферой. Сосуды располагаются в различных направлениях, причем артериальные и венозные сосуды, по которым кровь движется в противоположных направлениях, большей частью параллельны.
Эти сосуды сообщаются между собой через капилляры, поэтому в первом приближении можно считать, что гидростатическое давление крови в них, как в сообщающихся сосудах, взаимно уравновешивается, и в качестве модели можно рассматривать систему горизонтальных трубок.
В случае повреждения сосудистой стенки может образоваться сообщение сосуда с атмосферой, и тогда проявляется действие гидростатического давления крови. Общеизвестно, например, что для ослабления кровотечения из пораненного сосуда конечности ей следует придать возвышенное положение.
Течение крови в сосудистой системе в нормальных условиях имеет ламинарный характер. Оно может переходить в турбулентное при нарушении этих условий, например при резком сужении просвета сосуда. Подобные явления могут иметь место при неполном открытии или, наоборот, при неполном закрытии сердечных или аортальных клапанов. При этом появляются звуки, называемые сердечными шумами, которые являются одним из характерных признаков этого явления.
Работа, совершаемая сердцем, в основном складывается из работы при сокращении желудочков, главным образом левого. (Работа правого желудочка принимается равной 0,2—0,15 от работы левого.)
Работа сердечной мышцы при каждом сокращении левого желудочка затрачивается на сообщение объему выталкиваемой крови энергии, необходимой для его продвижения по всему кругу кровообращения. Эта энергия состоит из потенциальной энергии давления, которое должно быть создано вначале для преодоления сопротивления движению крови по всему ее пути, и кинетической энергии для сообщения массе крови необходимой скорости движения. На основании данных эта энергия может быть представлена формулой
где р — среднее давление, под которым кровь выбрасывается в аорту, р = 100 мм рт. ст=105 100/760 =1,3·104 Па; ρ = 1,05· 103 кг/м3 — плотность крови; — скорость крови в аорте, в состоянии покоя ; ударный объем крови в покое в среднем , Аж= 0,95 Дж
Учитывая работу правого желудочка, для сердца в целом найдем Ас=1,2∙Аж=1,14 Дж
Время сокращения желудочков Тогда мощность, развиваемая сердцем при сокращении, будет NC= Ас/tж=3,4 Вт
Считая в среднем 60 сокращений сердца в 1 мин, получим, что за 1 мин оно совершает работу .
При расчете работы сердца можно вместо ударного учитывать минутный Vмин объем крови, равный произведению ударного объема на число N сокращений сердца в 1 мин:
. В нашем примере мл/мин, или 4,2 л/мин.
При мышечной работе средней интенсивности минутный объем крови увеличивается примерно в пять раз, т. е. 20 л/мин. При этом соответственно возрастает скорость течения крови в аорте: . Тогда работа, совершаемая сердцем в 1 мин, будет Ас≈360 Дж.
Источник
