Модель идеального газа в сосуде
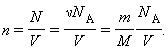
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма – частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
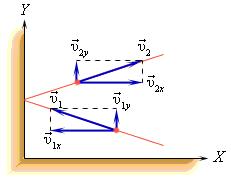
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
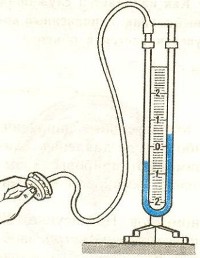
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый – для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

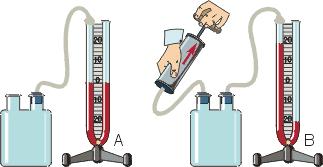
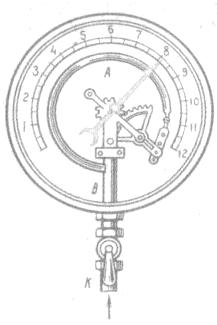
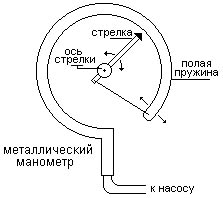
Металлический манометр – для измерения больших давлений.
Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 – масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 – средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим или
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Источник
Идеальный газ – это модель разреженного газа, в которой пренебрегается взаимодействием между молекулами. Силы взаимодействия между молекулами довольно сложны. На очень малых расстояниях, когда молекулы вплотную подлетают друг к другу, между ними действуют большие по величине силы отталкивания. На больших или промежуточных расстояниях между молекулами действуют сравнительно слабые силы притяжения. Если расстояния между молекулами в среднем велики, что наблюдается в достаточно разреженном газе, то взаимодействие проявляется в виде относительно редких соударений молекул друг с другом, когда они подлетают вплотную. В идеальном газе взаимодействием молекул вообще пренебрегают.
Теория создана немецким физиком Р. Клаузисом в 1957 году для модели реального газа, которая называется идеальный газ. Основные признаки модели:
- ·
расстояния
между молекулами велики по сравнению с их размерами; - ·
взаимодействие
между молекулами на расстоянии отсутствует; - ·
при
столкновениях молекул действуют большие силы отталкивания; - ·
время
столкновения много меньше времени свободного движения между столкновениями; - ·
движения
подчиняются законом Ньютона; - ·
молекулы –
упругие шары; - ·
силы
взаимодействия возникают при столкновении.
Границы применимости модели идеального газа зависят от рассматриваемой задачи. Если необходимо установить связь между давлением, объемом и температурой, то газ с хорошей точностью можно считать идеальным до давлений в несколько десятков атмосфер. Если изучается фазовый переход типа испарения или конденсации или рассматривается процесс установления равновесия в газе, то модель идеального газа нельзя применять даже при давлениях в несколько миллиметров ртутного столба.
Давление газа на стенку сосуда является следствием хаотических ударов молекул о стенку, вследствие их большой частоты действие этих ударов воспринимается нашими органами чувств или приборами как непрерывная сила, действующая на стенку сосуда и создающая давление.
Пусть одна молекула находится в сосуде, имеющем форму прямоугольного параллелепипеда (рис. 1). Рассмотрим, например, удары этой молекулы о правую стенку сосуда, перпендикулярную оси Х. Считаем удары молекулы о стенки абсолютно упругими, тогда угол отражения молекулы от стенки равен углу падения, а величина скорости в результате удара не изменяется. В нашем случае при ударе проекция скорости молекулы на ось У не изменяется, а проекция скорости на ось Х меняет знак. Таким образом, проекция импульса изменяется при ударе на величину, равную , знак «-» означает, что проекция конечной скорости отрицательна, а проекция начальной – положительна.
Определим число ударов молекулы о данную стенку за 1 секунду. Величина проекции скорости не изменяется при ударе о любую стенку, т.е. можно сказать, что движение молекулы вдоль оси Х равномерное. За 1 секунду она пролетает расстояние, равное проекции скорости . От удара до следующего удара об эту же стенку молекула пролетает вдоль оси Х расстояние, равное удвоенной длине сосуда 2L. Поэтому число ударов молекулы о выбранную стенку равно . Согласно 2-му закону Ньютона средняя сила равна изменению импульса тела за единицу времени. Если при каждом ударе о стенку частица изменяет импульс на величину , а число ударов за единицу времени равно , то средняя сила, действующая со стороны стенки на молекулу (равная по величине силе, действующей на стенку со стороны молекулы), равна , а среднее давление молекулы на стенку равно , где V – объем сосуда.
Если бы все молекулы имели одинаковую скорость, то общее давление получалось бы просто умножением этой величины на число частиц N, т.е. . Но поскольку молекулы газа имеют разные скорости, то в этой формуле будет стоять среднее значение квадрата скорости, тогда формула примет вид: .
Квадрат модуля скорости равен сумме квадратов ее проекций, это имеет место и для их средних значений: . Вследствие хаотичности теплового движения средние значения всех квадратов проекций скорости одинаковы, т.к. нет преимущественного движения молекул в каком-либо направлении. Поэтому , и тогда формула для давления газа примет вид: . Если ввести кинетическую энергию молекулы , то получим , где – средняя кинетическая энергия молекулы.
Согласно Больцману средняя кинетическая энергия молекулы пропорциональна абсолютной температуре , и тогда давление идеального газа равно или
. (1)
Если ввести концентрацию частиц , то формула перепишется так:
. (2)
Число частиц можно представить в виде произведения числа молей на число частиц в моле, равное числу Авогадро , а произведение . Тогда (1) запишется в виде:
. (3)
Уравнения (1), (2) и (3) – это разные формы записи уравнения состояния идеального газа, они связывают давление, объем и температуру газа. Эти уравнения применимы как к чистым газам, так и к смесям газов, в последнем случае под N, n и ν следует понимать полное число молекул всех сортов, суммарную концентрацию или полное число молей в смеси. Для чистого газа число молей , где М – масса газа, а μ – масса одного моля (молярная масса). Тогда уравнение (3) примет вид:
. (4)
Уравнение состояния в этой форме называют уравнением Клапейрона–Менделеева.
Рассмотрим частные газовые законы. При постоянной температуре и массе из (4) следует, что , т.е. при постоянной температуре и массе газа его давление обратно пропорционально объему. Этот закон называется законом Бойля и Мариотта, а процесс, при котором температура постоянна, называется изотермическим.
Для изобарного процесса, происходящего при постоянном давлении, из (4) следует, что , т.е. объем пропорционален абсолютной температуре. Этот закон называют законом Гей-Люссака.
Для изохорного процесса, происходящего при постоянном объеме, из (4) следует, что , т.е. давление пропорционально абсолютной температуре. Этот закон называют законом Шарля.
Эти три газовых закона, таким образом, являются частными случаями уравнения состояния идеального газа. Исторически они сначала были открыты экспериментально, и лишь значительно позднее получены теоретически, исходя из молекулярных представлений.
Источник
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма – частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.

Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый – для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума


Металлический манометр – для измерения больших давлений.
Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.


Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 – масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 – средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим или
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Источник
