Моделирование сосудов по давлению
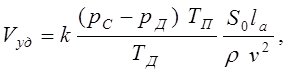
Доплер сосудов для начинающих (лекция на Диагностере)
Объект в движении меняет волны частоту. Когда кровяное тельце стремится К излучателю – отраженная частота выше, ОТ излучателя – отраженная частота ниже.
Источник и приемник УЗ-волны находятся в датчике. Прибор замеряет допплеровский сдвиг частоты: ΔF=(Fд-Fо), где Fд – частота датчик, Fо – отраженная частота.
Нажимайте на картинки, чтобы увеличить.
УЗ-волна ложится на вектор скорости под ∠α. ΔF определяет проекция вектора скорости на УЗ-луч (V·cosα): ΔF=2Fд·V·cosα/C, С – скорость звука в мягких тканях 1540 м/с.
Для оценки скорости кровотока используют уравнение Доплера: V=ΔF·C/2Fд·cosα. Когда УЗ-луч проникает в сосуд под ∠90° ⇒ cosα=0, невозможно оценить скорость кровотока.
Для ∠0-60° величина cosα от 1 до 0,5; для ∠60-90° величина cosα от 0,5 до 0. Коротко от 90° величина Vcosα мала ⇒ ΔF небольшой ⇒ скорость неточная.
Когда ∠α ниже 25°, УЗ-луч почти полностью отражается от стенки сосуда. Чтобы определить скорость потока, направляете УЗ-луч под углом 25-60°.
Дуплексное и триплексное сканирование сосудов
Три уровня УЗИ сосудов: серая шкала (В-режим), цветное доплеровское картирование (ЦДК) и спектральная доплерография (D-режим).
Дуплексное сканирование сосудов – В-режим и ЦДК, B-режим и D-режим; триплексное сканирование сосудов – В-режим, ЦДК и D-режим.
ЦДК кодирует скорость и направление в оттенки красного и синего: темные и светлые тона – низкие и высокие скорости. Когда зашкаливает cкорость, пропадает цвета чистота.
Радужные переливы (элайзинг) указывают высокоскоростной поток в месте стеноза. Настройте шкалу скорости: 4 см/с – низкая, 115 см/с – высокая, 39 см/с – правильная.
Энергетический доплер кодирует скорость, но не направление, в оттенки одного цвета; полезный в извитых сосудах и на маленьких скоростях.
Задача.
Спектр получают из ворот в центре сосуда. Вертикальная ось – шкала скорости; горизонтальная – время; базовая линия обрезает поток К и ОТ датчика.
Спектр может пересекать базовую линию; составляющие по разные стороны называют фазами. Спектр может быть моно-, би-, трех- и четырехфазный.
Как измерить скорость кровотока
1. Ворота поместите в центр сосуда (трэкбол), длину установите на 2/3-4/5 просвета (SVlength);
2. Угол между УЗ-лучом и осью сосуда 25-60°, курсор вдоль потока;
3. Спектр занимает 2/3-4/5 шкалы скорости (PRF), временная развертка на 2-3 цикла;
4. Для артерий спектр располагают выше базовой линии, для вен – ниже (Invert).
5. Отрегулируйте усиление (GAIN), чтобы контур спектра был четкий.
6. Обведите спектр и получите отчет – Vps, Ved, RI, PI и др.
Задача. УЗ-луч и сосуд под ∠90° (1) – спектр неясный; исправим наклон датчика (2) – PSV 43,3 см/сек; курсив вдоль потока (3) – правильная PSV 86,6 см/сек. RI и PI не требуют коррекции угла.
Количественные характеристики спектра
Vps – пиковая систолическая скорость;
Ved – максимальная конечная диастолическая скорость;
TAMX – усредненная по времени максимальная скорость кровотока;
TAV – усредненная по времени средняя скорость кровотока;
RI=(Vps-Ved)/Vps – индекс резистивности отражает сопротивление потоку далее места измерения;
PI=(Vps-Ved)/TAMX – индекс пульсативности отражает упругоэластические свойства артерий;
В воротной вене PI=PSV/EDV;
PI’=(Vps-Ved)/TAV – модифицированный индекс пульсативности;
SBI=(Vps-TAV)/Vps=1-TAV/Vps – индекc спектрального расширения отражает турбулентность потока;
SBI’=(Vps-TAV)/TAMX – модифицированный индекc спектрального расширения;
S/D – систолодиастолическое соотношение;
AT – время ускорения;
AI – индекс ускорения.
Задача. Измерение пиковая систолическая, максимальная конечная диастолическая скорости, TAMX, TAV для артерий с высоким и низким сопротивлением.
PSV и EDV высокие в месте стеноза; RI растет перед и падает после стеноза. После стеноза спектр имеет форму tardus-parvus: PSV поздняя – ТРТ>70 мс, PSV/TTP 0,7; в сосудах с низким сопротивлением в диастолу поток значимый, RI 0,55-0,7.
Сосуды с высоким сопротивлением: наружная сонная и артерии конечностей, а так же верхняя и нижняя брыжеечные артерии у голодного.
Сосуды с низким сопротивлением: внутренняя сонная, почечная, печеночная, яичковая артерии, а так же брыжеечные артерии у сытого.
Нормальная форма спектра в сосудах
Аномальная форма спектра в сосудах
Берегите себя, Ваш Диагностер!
Источник
Моделирование газа в физическом симуляторе
Дата публикации: 03.02.2015 2015-02-03
Статья просмотрена: 1417 раз
Библиографическое описание:
Данилов, О. Е. Моделирование газа в физическом симуляторе / О. Е. Данилов. – Текст : непосредственный // Молодой ученый. – 2015. – № 4 (84). – С. 20-26. – URL: https://moluch.ru//84/15493/ (дата обращения: 17.10.2020).
Учебные компьютерные модели (программы, предназначенные для обучения) позволяют наблюдать явления и процессы в динамике [3; 4; 6]. В то же время такие программы предоставляют возможность увидеть на экране компьютера абстрактные объекты и явления, которые в реальном мире не существуют, а являются лишь моделями реальных объектов и явлений [2]. Возможно создание таких моделей с помощью языков программирования высокого уровня и специальных компьютерных приложений [2; 3; 4; 6]. В последнее время получила широкое распространение постановка модельного эксперимента в так называемых виртуальных средах. Такое моделирование не требует от экспериментатора знания языков программирования и может быть использовано в обучении различным дисциплинам. В своей практике мы используем физический симулятор Algodoo (https://www.algodoo.com/).
Рис. 1. Создание стенки сосуда
Рассмотрим, как с помощью этого симулятора создать модель одноатомного газа [1, с. 4-14]. Напомним, что идеальный газ – это математическая модель газа (то есть абстракция), в которой в рамках молекулярно-кинетической теории предполагается, что: 1) потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объем частиц газа пренебрежимо мал (их можно считать материальными точками); 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда являются абсолютно упругими; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. Именно такой объект и будет создан нами в виртуальной среде. В расширенной модели идеального газа частицы, из которого он состоит, могут иметь более сложную форму (являться системой связанных материальных точек), что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц. Это также может быть реализовано с помощью программы Algodoo, но требует дополнительных усилий.
Рис. 2. Сосуд для газа
Начнем с того, что выключим (так это называется в Algodoo) гравитацию, выталкивающую силу и трение воздуха, то есть зададим параметры внешней среды. Затем создадим сосуд, в котором будет находиться газ. Симулятор позволяет создавать только двумерные модели, поэтому моделируемый нами газ будет плоским. В этом случае стенками сосуда будут обычные прямоугольники. Создаем первый прямоугольник (рис. 1), выбирая следующие его свойства: трение – 0, упругость – 1. Это нужно для того, чтобы столкновения молекул газа со стенками сосуда были абсолютно упругими. После этого клонируем (именно так называется действие в Algodoo, соответствующее созданию копии объекта) стенку с указанными свойствами три раза и размещаем получившиеся стенки сосуда так, как показано на рис. 2. Делаем их неподвижными, закрепляя на фоне окна программы с помощью специальной функции, имеющейся в выпадающем меню программы. Сосуд готов.
Рис. 3. Создание частицы газа
Следующий этап – создание газа внутри сосуда. Для этого создаем круг нужного диаметра с такими же свойствами, как и у стенок сосуда: трение – 0, упругость – 1 (рис. 3). Это и будет молекула газа. Задаем начальные характеристики движения: проекции начальной скорости на вертикальное и горизонтальное направления должны быть небольшими по величине, то есть находиться в некотором диапазоне, таком, что за небольшой промежуток, соответствующий минимальному шагу по времени, молекула газа не оказывалась вне сосуда. Это определяется экспериментальным образом (рис. 4). Затем клонируем молекулу нужное количество раз (рис. 5) и изменяем начальные скорости молекул таким образом, чтобы они как можно лучше соответствовали случайному распределению их абсолютных величин и направлений в пространстве (рис. 6).
Рис. 4. Наблюдение движения частицы газа
Рис. 5. Клонирование частиц газа
Рис. 6. Изменение скоростей частиц газа
Запускаем симулятор и наблюдаем движение частиц газа в сосуде (рис. 7). Модель готова. Усложнив ее, можно изучать различные процессы, протекающие в газах, такие, как диффузия и самодиффузия [6; 7, с. 19], расширение газа в пустоту, сжатие и расширение газа с помощью поршня [6] и др.
Симулятор позволяет создать и модель броуновского движения. Для этого необходимо создать броуновскую частицу – фигуру произвольной формы, имеющую существенно большие размеры и массу, чем молекулы газа (рис. 8). Чтобы движение в сосуде не прекращалось, необходимо вновь задать свойства для вещества, из которого состоит частица: трение – 0, упругость – 1. Также задаются начальные проекции скорости (рис. 9). Программа предоставляет возможность проследить траекторию движения объектов, поэтому задав соответствующий параметр в свойствах частицы, мы можем организовать наблюдение траектории ее движения (рис. 10 и 11).
Рис. 7. Наблюдение движения частиц газа
Рис. 8. Создание броуновской частицы
Специфика использования данного симулятора в процессе обучения физике может быть следующей. Во-первых, преподаватель может использовать симулятор для динамических демонстраций, что невозможно сделать с помощью традиционных наглядных пособий, используемых в обучении. Преимущество таких демонстраций очевидно. К тому же, они вызывают живой интерес у обучающихся и желание рассмотреть различные моделируемые ситуации. Во-вторых, существует возможность проведения лабораторного и индивидуального модельного эксперимента. Тем самым могут быть решены проблема недостатка оборудования и проблема проведения технически сложного и, в связи с этим, не всегда понятного обучающимся натурного эксперимента [5, с. 4-16].
Рис. 9. Задание характеристик броуновской частицы
Рис. 10. Наблюдение траектории движения броуновской частицы
Рис. 11. Сложный характер движения броуновской частицы
1. Антонова Н. П. Физика 10: Молекулярная физика: Рабочая тетрадь / Н. П. Антонова, О. Е. Данилов, Е. Г. Московкина; Под ред. В. В. Майера. – Глазов: ГГПИ, 1997. – 80 с.
2. Данилов О. Е. Использование компьютерных моделей при обучении физике / О. Е. Данилов // Проблемы школьного и дошкольного образования: Материалы III регионального науч.-практ. семинара «Достижения науки и практики – в деятельность образовательных учреждений». – Глазов: Глазов. гос. пед. ин-т, 2012. – С. 101-102.
3. Данилов О. Е. Компьютерное моделирование движения молекул газа / О. Е. Данилов // Проблемы учебного физического эксперимента: Сборник научных и методических работ. Выпуск 2. – Глазов: ГГПИ, 1996. – С. 78-80.
4. Данилов О. Е. Компьютерное моделирование идеального газа с помощью метода drag-and-drop / О. Е. Данилов // Учебный физический эксперимент: Актуальные проблемы. Современные решения: Программа и материалы одиннадцатой Всероссийской научно-практической конференции. – Глазов: ГГПИ, 2006. – С. 32.
5. Данилов О. Е. Лабораторный практикум: Молекулярная физика и термодинамика. Рабочая тетрадь студента / О. Е. Данилов. – Глазов: ГГПИ, 2007. – 84 с.
6. Данилов О. Е. Разработка обучающих программ с помощью инструментов для создания компьютерных игр / О. Е. Данилов // Молодой ученый. – 2014. – № 3. – С. 899-901.
7. Данилов О. Е. Физика 7: Строение вещества. Взаимодействие тел: Рабочая тетрадь / О. Е. Данилов, Е. Г. Московкина; Под ред. В. В. Майера. – Глазов: ГГПИ, 1997. – 80 с.
Источник
Источник
1.1.2. Модели функционирования сердечно-сосудистой системы
1.1.2.1. Модель О. Франка.
С позиции механики, точнее, гидродинамики, сердечно-сосудистую систему можно представить как совокупность следующих элементов:
1) ритмически работающий насос (сердце),
2) камера стабилизации давления (аорта и крупные артерии),
3) камера сопротивления (периферические сосуды),
4) камера распределения крови в тканях (капиллярная сеть),
5) камера емкости (венозный сосудистый отрезок).
Одной из первых моделей сердечно-сосудистой системы, построенной на основе таких представлений, является модель О. Франка (1899 г.).
В модели О. Франка система крупных сосудов артериальной части большого круга кровообращения моделируется одной упругой камерой, а система мелких сосудов – жесткой трубкой. Сердце представляется механическим насосом, соединенным с упругой камерой клапаном (рис.1. 6).
Работая в рамках модели О. Франка, можно найти формулу для оценки ударного объема крови – одного из важных параметров состояния сердечно-сосудистой системы. Ударным объемом крови называют объем крови, выбрасываемый левым желудочком сердца в аорту за период систолы.
Согласно модели О. Франка, объем крови, выходящий из сердца со скоростью Q (объемная скорость) за время dt (dt®0), равен сумме изменения объема крови в упругой камере (dV) и объема крови, протекающего через жесткую трубку за время dt со скоростью Q0:
Ударный объем крови по определению равен:
где Тп- период пульса.
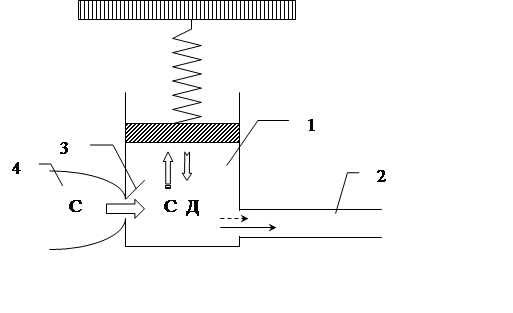 |
Рис.1. 6. Модель О. Франка.
1 – упругая камера (крупные артерии), представляющая собой цилиндр с поршнем, соединенным с упругой пружиной;
2 – жесткая трубка (периферические сосуды);
3 – клапан;
4 – насос (левый желудочек сердца).
Стрелки С и Д показывают направление поступления крови в разные части системы в период систолы и диастолы (соответственно).
С учетом упругих свойств крупных сосудов и законов движения жидкости по жесткой трубе формула для определения ударного объема крови выглядит следующим образом:
(1.3)
где k – коэффициент пропорциональности, введение которого связано со сделанными упрощениями; pC, pД – систолическое и диастолическое давления;
S0 – эффективная площадь поперечного сечения крупных артерий; lа – эффективная длина крупных артерий; TП, TД – период пульса и период диастолы соответственно; r – плотность крови; v – скорость крови.
Хотя формула (1.3) отражает основной характер зависимости ударного объема крови от вышеуказанных параметров, однако, вследствие множества упрощений, сделанных при ее выводе, она не может использоваться для количественных расчетов в медицинской практике. Существуют также трудности в измерениях на практике некоторых параметров, входящих в формулу, что делает ее использование целесообразным только в академических целях.
1.1.2.2. Гидродинамическая модель движения крови по кровеносному руслу.
Можно моделировать функционирование отдельных элементов сердечно-сосудистой системы. Рассмотрим модель движения крови по кровеносному руслу на основе законов механики. Пусть кровь по кровеносному руслу распространяется как жидкость в жесткой трубе. Кроме того, в продвижении крови по кровеносному руслу участвуют упруго деформирующиеся стенки сосудов.
Представим кровеносный сосуд как трубку с радиусом просвета (поперечного сечения) r. Движение малого объема крови (цилиндра – радиусом r и высотой dx) (рис.1.7), описывается вторым законом Ньютона (первое уравнение системы 1.4). Давление крови внутри сосуда уравновешивается силой упругости стенок сосуда (второе уравнение системы 1.4).
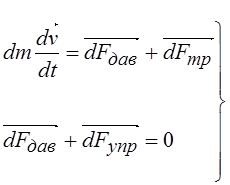 (1.4)
(1.4)
где dm – масса объема крови, v – скорость, dFдав – сила давления, dFтр – сила вязкого трения, dFупр – сила упругости.
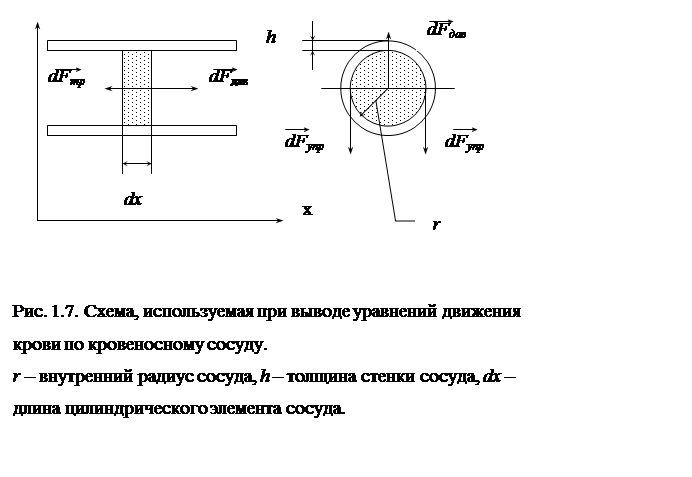
Рассмотрим первое из уравнений системы (1.4). Возьмем проекцию этого уравнения на ось x. Учтем, что
где r – плотность крови, S – площадь просвета сосуда (S=pr2), dp»Dp=p2-p1 – изменение давления на участке dx в связи с малостью этого участка приблизительно равно дифференциалу функции давления.
Для элементарного объема крови сила трения является силой вязкого трения, которую можно рассчитать по формуле Ньютона с использованием формулы Пуазейля:
где h – вязкость крови, Q=S.v – объемная скорость крови.
Тогда первое уравнение системы (1.4) с учетом введенных величин можно записать в виде:
Рассмотрим второе уравнение системы (1.4).
Плоскостью, проходящей через диаметр, условно разделим рассматриваемый объем крови и прилегающие к нему стенки сосуда на две половины (рис. 1.7). Образовавшееся сечение имеет площадь 2rdx. На эту площадь действует сила давления
dFдав=p.2rdx.
Силы давления стремятся разъединить обе половинки сосуда, в результате чего в сосудистой стенке возникают силы, препятствующие этому – упругие силы:
dFупр= s .2hdx,
где s- тангенциальное напряжение в стенке сосуда, 2hdx – сумма площадей продольных сечений стенки, к которым приложены упругие силы.
dFдав=dFупр,
p2rdx=s .2hdx,
pr=sh Þ p=sh/r.
Учитывая закон Гука (ds=Edr/r, где Е – модуль упругости Юнга) и выражение площади поперечного сечения сосуда (S=pr2, dS=2prdr), найдем дифференциал функции давления:
Разделим левую и правую части этого уравнения на dt и учтем, что dS= -dQ dt/dx:
Тогда система из системы уравнений (1.4) получим систему уравнений (1.5):
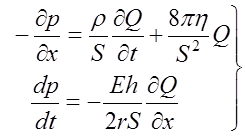 (1.5)
(1.5)
Система уравнений (1.5) описывает движение крови по кровеносному сосуду в рамках механического подхода. Система состоит из двух уравнений и содержит две неизвестные (Q и р), поэтому разрешима. Решение системы уравнений (1.5) выходит за рамки нашего курса, поэтому здесь приведем лишь конечные формулы, являющиеся решением данной системы уравнений.
Источник
Расчет сосуда под давлением
Автор Leadstar, 07.12.15, 13:41:50
« предыдущая – следующая »
0 Пользователей и 1 гость просматривают эту тему.
Вниз Страницы 1 2 3 4 5 6
А есть ещё радиальные силы от резьбы…
P.S.: “Старослужащие”! Пожалуйста, не спешите! Пусть “молодёжь” хорошо подумает и смело выступит!
Что, молодЁжь, страшно?! Это хорошо, если страшно! Если “инженер” – инженер, то страх – его неразлучный спутник… В принципе, не так всё и страшно… Если аккуратно посчитать в соответствии с приведённой схемой, то ориентировочное значение растягивающего напряжения составит 1900кгс/кв.см. Это: с учётом коэф. “нераскрытия стыка” = “1”, в предположении, что отсутствуют ударно-волновые процессы ( приведшие к катастрофе на СШГЭС )… В строительстве вполне допускается работа конструкций за “пределами” предела упругости. Иногда: с последствиями наподобие “Трансвааля”… Сам, слава богу, не проверял, но бают: струя масла под давлением 250техн. атм. с расстояния в полметра пробивает ладонь…
Цитата: Ё
Сам, слава богу, не проверял, но бают: струя масла под давлением 250техн. атм. с расстояния в полметра пробивает ладонь…
Бают Через пол метра там не будет 250 атм, более того – когда струя вышла в атмосферу, давление там упало до атмосферного
А вот скорость струи – другое дело, но это не сколько от давления, сколько от потока зависит. Это как у пули – дело в скорости и массе, а не давлении газов в стволе.
ЗЫ А давление в 200 атм – это обычное давление, простой насос для смазки его спокойно выдает (новый и 400 может выдать, пока не сношен).
Молодой человек! У Вас есть что “по делу”?! Или Вы привыкли “ля-ля” справлять”?!
Старый человечек, вы что – уже ревнуете, что еще кто-то кроме вас поучает, да еще кого – лично вас?!!!
ЗЫ во первых, близко к делу, во вторых – комментарий к вашему “не по делу”
Добрый вечер! Подскажите, пожалуйста, методику расчета выгибания фланца поз 1 (придание бочкообразности). Представим, что левая и правая стороны заглушены.
Насколько я понимаю, сначала нужно высчитать силу, которая будет приложена к фланцу давлением 21 МПа. Площадь приложения считать по резиновому кольцу круглого сечения (200мм). Площадь круга = 31415 мм2.
F=P*S. F= 21 Н/мм2 (МПа) * 31415мм2= 659715Н. Материал, например, имеет сигму временную около 600 МПа.
Дальнейший расчет вводит в ступор. Задача – либо подобрать материал с определенной сигмой временной, либо увеличить толщину фланца, либо и то и другое.
Тут вопрос скорее не в расчете а в вашей картинке – такое соединение я считаю неправильным для указанного давления – 21 МПа – указанное давление не соответствует изображенному соединению – все госты на подобные фланцы указывают максимальное рабочее давление в 20 МПа, и более того применение резиновых колец на такое давление во фланцах недопустимо. Для давлений от 20 до 100 Мпа используются например резьбовые фланцы по ГОСТ 9399 с линзовыми прокладками которые устанавливается между труб по ГОСТ 9400.
По ГОСТ 28919 фланцы и 21, и 35, и даже 105 МПа держат, с прокладками 8угольного сечения либо овального. Конструкция верная, это середина дисковой задвижки, которые широко распространены. Резиновые кольца в статике держат до 50МПа.
Так что вопрос именно в подборе мех. свойств и размеров фланца.
Ровно то, что Вам нужно: https://chem21./page/177132188005196222048097114165008165099255164228/
(Уплотнение фланцев кольцами КРУГЛОГО сечения при пульсирующем давлении до 300 атм. применяется с 80-х годов прошлого века даже в банальных сельхозмашинах – трансмиссия ГСТ-90. Так вот там есть проблема: фланцы малы, а трубы – жЁсткие. И не всегда получается надЁжное прижатие фланцев.)
Здесь основной момент: а) нераскрытие стыка более какой-то величины; б) отсутствие ползучести материалов фланца и болтов.
Это конечно все хорошо. Но мой основной вопрос в расчете именно на вздутие фланца. Остальное все посчитано, испытано, все работает.
Резиновые кольца держат давление 35МПа в данной конструкции при испытаниях (рабочее же будет 21макс). Фланец же немножко поддувает.
Как расчитать минимально необходимую толщину фланца при известном временном сопротивлении, чтобы его не начало выгибать – этот вопрос открыт. Логично предположить, что если фланец будет рассчитан и не будет выгибаться, то резиновое уплотнение станет еще надежнее.
Цитата: Leadstar от 21.01.17, 19:54:43
…
Как расчитать минимально необходимую толщину фланца при известном временном сопротивлении, чтобы его не начало выгибать – этот вопрос открыт. …
Конечно: ОТКРЫТ! А Вы как хотели?! В советские времена над такими вопросами целые институты работали! Для назначения КОЭФФИЦИЕНТОВ ЗАПАСА! Что значит: “его не начало выгибать”?! Выгибать его будет В ЛЮБОМ СЛУЧАЕ! Весь вопрос: а) НА СКОЛЬКО и б) какие при этом получаются ДЕЙСТВУЮЩИЕ напряжения? НА СКОЛЬКО – это: сможет ли работать рез. кольцо? А ДЕЙСТВУЮЩИЕ напряжения – это: как будет идти накопление деформаций с течением времени? ( Или, вообще: когда произойдЁт усталостное разрушение? ) И здесь: самый верный выбор – смотреть на опробованные конструкции и считать, какие там получаются РАСЧЁТНЫЕ напряжения. А также: смотреть материалы по испытаниям тех сплавов, из которых будет делаться Ваша конструкция. С учЁтом того, что там у Вас – сварка?
Для того Вы и ИНЖЕНЕР, чтобы ПРИНИМАТЬ РЕШЕНИЯ!
P.S.: и потом: для одних материалов “сигма врем.” – характеристический показатель, а для др. – сугубо теоретическая величина.
Да верно, с таким гостом не сталкивался – так что конструкция норм., а по поводу чтобы не выгибало фланец, можно сделать расчет по ГОСТ Р 52857.2-2007 – п. 7.2 схема 11 по типу как плоская крышка с отверстием ослабляющим – ну и по результатам расчета взять толщину фланца, для успокоения – сделать трехмерную модель и нагрузить ее давлением – в солиде или апм перепроверить. несложная задача. я бы начал с модельки и понагружал ее давлением – там будет видно сразу насчет приблизительной толщины
ЦитироватьВыгибать его будет В ЛЮБОМ СЛУЧАЕ!
Разве? Необходимое условие – чтоб не выгибало фланец более, чем на величину допуска на соединения резинового кольца с канавкой.
При достаточной толщине внутренние напряжения материала не будут превышать предел прочности на изгиб/растяжение или даже не знаю что там за деформация происходит, комплексная какая-то. При этих условиях первый пункт выполним, фланец не выгнет за пределы допусков. Или я где-то неверно мыслю? Понимаю, что все нюансы не учесть, и эффект бабочки сыграть может Но хотя бы методику теоретически вычислить варианты быть должны.
westdm
Да, прорисовал модель, установил APM, день поковырялся в нем. Комп завис) Разбил на слишком мелкие сегменты. Увеличил размер сегментов, жду)
В ГОСТах на фланцы был расчет, там и с выворачиванием было.
Так же в инете книжка есть – Резьбовые и фланцевые соединения. Биргер, Иосилевич, 1990 г.
А не хотите сделать плавный переход от фланца к трубе. большой фаской? Жесткость возрастет, а масса не атк сильно.
Можно еще сделать уплотнения меньшего диаметра, вокруг самих труб – тогда площадь резко уменьшится, а с ней и нагрузки. Зачем вообще такой огромный фланец к таким небольшим трубам?
Либо сделать поясок и уплотнение по цилиндру – стык раскрываться почти не будет.
ЗЫ резиновые О-ринги и 100 МПа держат, используем, но правда резины потверже (хотя там всеравно фторопластовые кольца подложены) и по цилиндру уплотнение.
Восьмиугольные стальные кольца применять пробовали, но проблем больше – они твердоваты (самодельные, могут не отжигать) и уплотняют плохо (пришлось под них капролоновые подкладывать), проще оказалось О-ринги по цилиндру применить. Хотя может с покупными восьмигранными и норм было бы.
Kirilius83
Фланцы такого диаметра необходимы для того, чтобы внутри них, в полости, вращался шибер – это задвижка дисковая, нуждающаяся в доработке.
Про плавный переход – так и поступлю. Уже прорисовал в АПМ, но возникли вопросы.
Про уплотнения вокруг труб не понял. Труба и фланец – единая деталь (отливка).
Появился вопрос по APM – он всегда визуально деформирует детали от нагрузки, независимо от механических свойств материала?
Цитата: Leadstar от 23.01.17, 15:09:22
Kirilius83
…
Появился вопрос по APM – он всегда визуально деформирует детали от нагрузки, независимо от механических свойств материала?
Что бы это значило…
ЦитироватьЧто бы это значило…
Вот. В самом АПМ не разобрался, где смотреть материал. Помню, в одной из операций у меня вылезло сообщение, что то вроде “не удалось получить доступ к библиотеке материалов, поэтому выбран материал по умолчанию – сталь”. Какая сталь в сообщении указано не было.
Поэтому вопрос можно расшифровать так: на картинке показано, как деформируется тело при превышении определенных нагрузок, или это выгибание напрямую связано с механическими свойствами материала, заданным “по умолчанию”?
такими программами как апм и прочие расчетные приложения нужно пользоваться только вместе с классическим расчетом( я выше писал ГОСТ), в расчетах МКЭ много подводных камней и нужны знания (там и разбиение влияет и типы элементов в различных зонах) апм весьма примитивная в этом плане программа – хотите серьезного расчета МКЭ – это ансис, но там нужно знания как что считать, очень много специфики, а в таком серьезной деле как изделия с высоким давлением – пользуйтесь формулами и гостовскими методиками расчета! не надейтесь на МКЭ!
Цитировать( я выше писал ГОСТ)
В том ГОСТе тоже не полное соответствие с моим вариантом, Мой вариант ослаблен отверстием, но усилен трубой снаружи этого отверстия. Если б не отверстие, то один в один. Но и по этой методике посчитаю, спасибо.
Вверх Страницы 1 2 3 4 5 6
Источник
