Моделирование течения крови в сосудах
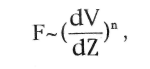
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Доль А.В. 1 Гуляев Ю.П. 1 Иванов Д.В. 1
1 ФБГОУ ВПО «Саратовский государственный университет имени Н.Г. Чернышевского»
В работе рассматриваются новые подходы к моделированию гемодинамики крупных кровеносных сосудов, которые позволяют сократить число основополагающих гипотез. Предложен алгоритм решения основной замкнутой системы уравнений динамики кровотока, а также приведены результаты расчетов начальных точек дисперсионных кривых для дисперсионного уравнения, полученного в процессе решения данной системы.
математическое моделирование
артерия
упругие стенки
осесимметричное движение крови
1. Моделирование виллизиевого круга человека в норме и при патологии / Д.В. Иванов, А.В. Доль, О.Е. Павлова, А.В. Аристамбекова // Российский журнал биомеханики. 2013. Т. 17. № 3(61). С. 36-49.
2. Педли Т. Гидродинамика крупных кровеносных сосудов / Т. Педли. М.: Мир, 1983. 400 с.
3. Смертность от болезней системы кровообращения в России и экономически развитых странах / В.И. Харченко, Е.П. Какорина, М.В. Корякин и др. // Российский кардиологический журнал. 2005. № 2. С. 5-18.
4. Berger S.A., Jou L.D. Flows in Stenotic Vessels // Annu Rev Fluid Mechanics. 2000. Vol. 32. P. 347-384.
5. Bruin A. Numerical Simulation of blood flow through elastic vessels // Master Thesis, Department of Mathematics University of Groningen. 2003. 24 p.
6. Chen J., Lu X.-Y. Numerical Investigation of the non-Newtonian Pulsatile Blood Flow in a Bifurcation Model With a Non-Planar Branch // Journal of Biomechanics. 2006. Vol. 39. P. 818-832.
7. Tambasco M., Steinman D.A. Path-Dependent Hemodynamics of the Stenosed Carotid Bifurcation // Annals of Biomedical Engineering. 2003. Vol. 31. P. 1054-1065.
8. Numerical issues of modelling blood flow in networks of vessels with pathologies / S. Simakov, V. Salamatova, Yu. Ivanov, T. Dobroserdova // Russian Journal of Numerical Analysis and Mathematical modeling. 2011. Vol. 26. Iss. 6. P. 1-18.
Введение
По статистике, сердечно-сосудистые заболевания являются одной из основных причин инвалидности и смерти жителей большинства современных развитых стран [3]. На долю смертности от заболеваний сердечно-сосудистой системы в общем приходится до 60% от общего числа умерших.
Нередко для восстановления кровообращения в пораженных сосудах помимо медикаментозного лечения проводятся реконструктивные операции, и часто невозможно объективно оценить, какой тип оперативного вмешательства будет оптимальным для конкретного пациента, а также насколько близок будет кровоток в сосуде к нормальному после операции. Основная проблема при выполнении таких расчетов состоит в определении механических свойств стенок сосудов, параметров кровотока и др.
Еще одной важной проблемой при прогнозировании результатов лечения является скорость расчетов: как правило, большинство современных математических моделей требуют численного решения, причем во многих случаях вычисления получаются затратными по времени и требуют довольно мощные компьютеры [8]. При этом снижение времени расчетов путем упрощений может привести к неточности полученных результатов, что, безусловно, недопустимо [5].
Часто для численных расчетов применяют метод конечных элементов. Однако решение задач гемодинамики с помощью МКЭ требует больших затрат по времени [5].
Таким образом, актуальной является задача построения математической модели гемодинамики, которая бы достаточно полно описывала движение крови в кровеносных сосудах, учитывая взаимодействие жидкости со стенкой, и являлась легко адаптируемой под конкретного пациента.
Материалы и методы
Рассмотрим осесимметричное движение крови, которая принимается вязкой несжимаемой жидкостью, в круглом сосуде постоянного радиуса R. Движение происходит в цилиндрической системе координат (x, r, θ), причем ось x совпадает с осью симметрии потока [2]. Материал стенки считаем идеально упругим, изотропным.
Основная система уравнений динамики кровотока в гибких цилиндрических сосудах в таком случае будет иметь вид:
, (1)
, (2)
, (3)
, (4)
, (5)
, (6)
, (7)
, ,
где p – давление; ρ – плотность крови; μ – вязкость крови; vx – осевая компонента скорости крови; vr – радиальная компонента скорости крови; R – радиус сосуда; t – время; u, w – перемещения стенки в продольном и поперечном направлениях; Sʹ, Tʹ – силы натяжения в окружном и продольном направлениях соответственно; S0, T0 – начальные значения сил натяжения в окружном и продольном направлениях; E – модуль Юнга стенки; ν – коэффициент Пуассона; h – толщина стенки сосуда; ρ0 – массовая плотность материала стенки сосуда.
На стенке записываем условия кинематического контакта стенки сосуда с жидкостью:
(8)
В случае моделирования гемодинамики крупных кровеносных сосудов в большинстве современных работ кровь полагается ньютоновской жидкостью [4, 7]. При этом в [6] показано, что разница значений (в случае крупных кровеносных сосудов), которые получаются для ньютоновской и неньютоновской жидкостей, не превышает 10%.
Уравнения (4)-(7) позволяют учесть податливость сосудистой стенки, а контактные условия (8) позволяют учесть взаимодействие стенки с потоком.
Такой подход к моделированию гемодинамики широко известен, однако основная система уравнений в этом случае не позволяет учесть конвективную составляющую ускорения частиц жидкости, а это, в свою очередь, для сосудистого русла с несколькими узлами бифуркации может оказать существенное влияние на результаты расчетов.
Основная система уравнений динамики вязкой несжимаемой жидкости в кровеносных сосудах с гибкими стенками в трехмерной постановке может быть записана в виде уравнений для направленных потоков.
Будем, как и раньше, полагать, что задача осесимметрична, а кровь является ньютоновской жидкостью.
Для направленных потоков жидкости в тонких трубках с упругими стенками на основе известного способа линеаризации возможен учет конвективного ускорения частиц жидкости в рамках линейной теории. В случае осесимметричных направленных потоков уравнения Навье-Стокса имеют следующий вид:
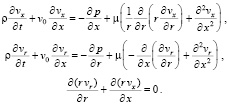 (9)
(9)
Здесь v0 – основная скорость направленного потока, вокруг которой происходит малая пульсация составляющих скоростей: vx = v0 + vʹ; vr = vʹ.
Динамические уравнения осесимметричных колебаний предварительно натянутой круглой цилиндрической оболочки записываются в виде:
(10)
где .
Условия «прилипания» частиц жидкости к стенкам сосуда заменим условием стесненного их скольжения по поверхности контакта:
(11)
λ – коэффициент вязкого трения материала оболочки и жидкости.
Рассмотрим систему уравнений (9), (10) с контактными условиями (11). Умножим уравнение (1) на r и продифференцируем по x. Далее второе уравнение системы также умножим на r и продифференцируем по r, после чего сложим левые и правые части полученных уравнений. В результате получим уравнение для давления:
. (12)
Запишем преобразованную систему уравнений:
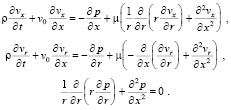 (13)
(13)
Для дальнейшего упрощения предложенной системы уравнений в трехмерной постановке можно вместо уравнений Навье-Стокса (9) использовать уравнения Эйлера для описания движения направленного потока идеальной несжимаемой жидкости, полагая при этом, что вязкое стесненное трение жидкости о стенку сосуда будет происходить в бесконечно тонком слое (погранслой) на контактной поверхности.
(14)
Вязкие свойства жидкости в погранслое будут описываться упрощенным одномерным уравнением, записанным на основании первого уравнения Навье-Стокса:
. (15)
При этом на границе погранслоя функция давления может испытывать конечный скачок. Касательные напряжения на стенке будут иметь вид:
(16)
Тогда уравнения движения оболочки примут вид:
(17)
В качестве контактных условий для идеальной жидкости можно взять условия непроницаемости стенки и условия прилипания частиц жидкости вдоль стенки:
. (18)
Из системы уравнений (14)-(17) путем простых преобразований может быть получено уравнение для давления в виде (12).
Запишем преобразованную систему уравнений:
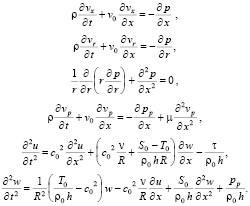 (19)
(19)
Система (19) с контактными условиями (18) представляет собой упрощенный вариант системы уравнений динамики кровотока в сосудах с упругими стенками, так как уравнения Навье-Стокса здесь заменяются уравнениями Эйлера для идеальной жидкости, которые имеют более простой вид.
Решение основной системы уравнений для случая пульсирующего кровотока как для системы (9)-(10), так и для системы (19) можно искать в виде простых гармонических волн:
, (20)
, (21)
где ω – частота пульсации кровотока, χ – волновое число.
Подставляя выражения (21) в уравнения движения жидкости основной системы, получим базовые решения для амплитуд компонент скорости и давления. В этом случае сумма базовых решений для каждой волновой гармоники даст общее решение основной системы.
Неизвестные константы необходимо определять из контактных условий, уравнений движения стенки, а также из граничных условий на входе и выходах из сосудистой системы. Это напрямую связано с решением дисперсионных уравнений, возникающих при подстановке выражений (20) в основную систему.
Были получены начальные точки (рис. 1 и 2) дисперсионных кривых для дисперсионного уравнения, полученного при решении системы (1)-(7). На рисунках значения по осям а и b – это действительная и мнимая части волнового числа.
Используя полученные точки в качестве начальных приближений для построения решения дисперсионного уравнения, можно построить необходимые дисперсионные кривые, что позволит завершить решение полной краевой задачи с учетом краевых и контактных условий и найти необходимое число констант интегрирования.
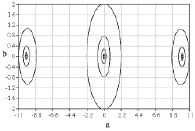
Рис. 1. Начальные точки дисперсионных кривых в случае малой вязкости
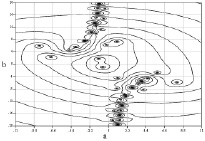
Рис. 2. Начальные точки дисперсионных кривых в случае большой вязкости
Такой алгоритм поиска общего решения системы (1)-(7) вполне подходит для решения систем (9)-(10) и (19). Таким образом, предложенные математические модели могут использоваться для исследования кровотока в системе кровеносных сосудов.
Результаты и обсуждение
Предложенные варианты постановки задач гемодинамики в системе кровеносных сосудов позволяют уменьшить количество основополагающих предположений и упростить основную систему уравнений. В случае, когда проводится учет направленных потоков жидкости, отпадает необходимость пренебрежения конвективной составляющей ускорения частиц, что повышает точность результатов.
Новый вид кинематических контактных условий стесненного скольжения (11), по мнению авторов, более адекватно описывает процесс взаимодействия потока со стенкой. В реальном сосуде в случае выполнения условий прилипания частиц неизбежным был бы процесс образования атеросклеротических отложений, который является патологическим. Таким образом, математические модели, в которых взаимодействие крови со стенкой описывается подобным образом, не могут достоверно описывать процесс гемодинамики.
Замена уравнений Навье-Стокса уравнениями Эйлера в системе (19) существенно упрощает основную систему, при этом уравнение для тонкого погранслоя вблизи стенки сосуда (15) позволяет учесть все возникающие в этой области процессы.
Таким образом, предложен ряд упрощений и уточнений, позволяющий более точно и адекватно моделировать движение крови в системе кровеносных сосудов человека.
Выводы
Предложены новые варианты постановки задач о движении крови в сосудах с упругими стенками, позволяющие уменьшить количество основополагающих гипотез и, тем самым, повысить строгость и реалистичность предлагаемых математических моделей.
Кроме того, предложен новый вид кинематических контактных условий, позволяющих более точно описать процесс взаимодействия потока крови с сосудистой стенкой.
Библиографическая ссылка
Доль А.В., Гуляев Ю.П., Иванов Д.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ КРОВИ В СИСТЕМЕ СОСУДОВ С УПРУГИМИ СТЕНКАМИ // Успехи современного естествознания. – 2014. – № 9-1. – С. 79-84;
URL: https://natural-sciences.ru/ru/article/view?id=34193 (дата обращения: 07.06.2021).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Источник
. . . . .
, , , , .
https://www.allbest.ru/
̻
( 12)
: . -03-1 ..
: . . . ..
2006
:
1. , , 1.1 .
2. .
3. : , , .
4. . ( 10).
5. . .
6. .
1.1
35 ., 6 ., 4 , 7 , 5 .
, , , . , , , , .
.
– . .
, , LAB 7.0.1 MathWorks, Inc.
1.
2.
2.1
2.2
2.3
3. .
3.1 .
3.2
3.3
1
2
. m-,
. m-,
. m- F-
, . , , , . , , .
.
. .
: . , . .
1.
1 2 .
( ), , . , , , , , . , , , , ( ). , , , , . .
. () (), . -, .
: , . . , . ( ), . , . , , . , , , , – , , .
– . , . – , , .
. . , . , , , , , – . , , , , . , . , , , , . . , , , , , , . , , – . , , .. .
. , .. . () ( ) . . . , , , – . , . , . () . ( ) .
. 2,5 . , , . , . , , – , . , ( ) . . – – , , , . – , – ; , .
, , . , , , , . , . ; , , . – , , .
, , , . ; , (), (7 ).
. , , . 5% , . , , , . , . , ( ) . () (36,8-37). , , ; , (). , , , , , . .
. , , . , , . , . , , , : , ; , ; , .
, – , , . , .
() , , , , . , , , – , .. . – , , .
2.
2.1
, , . 5 – 10 /. , (0,3) 1,5 – 3,00, . , . . (0,3 – 0,5 /) . , . , (V), .
(2.1)
– – ;
0 – ;
– , ;
w – , –
(2.2)
– ;
h – ;
– ;
d – .
2.2
2.1. [1,5]
2.1
, | Dmax=16.60 Dmin=9.55 | Dmax=5.73 Dmin=3.18 | Dmax=8.28 Dmin=4.77 |
, | 13 | 9 | 45 |
, | 0.78 | 1.32 | 0.16 |
, /3 | 600 | 600 | 600 |
, | 2.40 | 1.50 | 0.90 |
, / | 72 | 72 | 72 |
, | 60 | 30 | 220 |
, / | 45 | 45 | 45 |
: – – | 115 75 | 130 87 | 127 83 |
2.3
:
2.1
2.2
:
2.3
2.4
:
2.5
2.6 –
m- ( ).
3. .
3.1 .
, , . (P) :
(3.1)
k – ;
V0 – .
(Q). Q-0. , . .
(3.2)
, .
:
(3.3)
1 2 – ;
l – ;
R – ;
– .
– .
(3.4)
:
, (3.5)
– ;
– .
, =0, (3.3) :
(3.6)
–
(3.7)
, ( ). . , . .
, .
Q=0
.
(3.8)
, .
3.2
:
3.1
P1=6552 P2=6555 P3=6557 P4=6561 P5=6563 P6=6566 P7=6570 P8=6573 P9=6575 P10=6578 | t1 = 3.1887 t2 = 3.1800 t3 = 3.1748 t4 = 3.1652 t5 = 3.1608 t6 = 3.1546 t7 = 3.1469 t8 = 3.1414 t9 = 3.1378 t10 = 3.1327 | T = 3.1887 3.1800 3.1748 3.1652 3.1608 3.1546 3.1469 3.1414 3.1378 10.0000 | X = 1.0000 3.1887 1.0000 3.1800 1.0000 3.1748 1.0000 3.1652 1.0000 3.1608 1.0000 3.1546 1.0000 3.1469 1.0000 3.1414 1.0000 3.1378 1.0000 10.0000 | Y = 8.7875 8.7880 8.7883 8.7889 8.7892 8.7897 8.7903 8.7907 8.7910 8.7915 |
B = 8.7883
0.0364
b1 = 8.7883
b2 = -0.0364
y=8.78-0.03x
:
3.2
P1=6544 P2=6547 P3=6549 P4=6552 P5=6554 P6=6556 P7=6570 P8=6574 P9=6576 P10=6579 | t1 = 3.2269 t2 = 3.2075 t3 = 3.1991 t4 = 3.1887 t5 = 3.1828 t6 = 3.1773 t7 = 3.1469 t8 = 3.1396 t9 = 3.1361 t10 = 3.1310 | T = 3.2269 3.2075 3.1991 3.1887 3.1828 3.1773 3.1469 3.1396 3.1361 3.1310 | X = 1.0000 3.2269 1.0000 3.2075 1.0000 3.1991 1.0000 3.1887 1.0000 3.1828 1.0000 3.1773 1.0000 3.1469 1.0000 3.1396 1.0000 3.1361 1.0000 3.1310 | Y = 8.7863 8.7868 8.7871 8.7875 8.7878 8.7881 8.7903 8.7909 8.7912 8.7916 |
B = 8.9770
-0.0593
b1 = 8.9770
b2 =-0.0593
y=8.97-0.05x
:
3.3
P1=6547 P2=6550 P3=6552 P4=6556 P5=6559 P6=6562 P7=6565 P8=6568 P9=6571 P10=6575 | t1 = 3.2075 t2 = 3.1954 t3 = 3.1887 t4 = 3.1773 t5 = 3.1699 t6 = 3.1630 t7 = 3.1567 t8 = 3.1507 t9 = 3.1450 t10 = 3.1378 | T = 3.2075 3.1954 3.1887 3.1773 3.1699 3.1630 3.1567 3.1507 3.1450 3.1378 | X = 1.0000 3.2075 1.0000 3.1954 1.0000 3.1887 1.0000 3.1773 1.0000 3.1699 1.0000 3.1630 1.0000 3.1567 1.0000 3.1507 1.0000 3.1450 1.0000 3.1378 | Y = 8.7868 8.7872 8.7875 8.7881 8.7886 8.7891 8.7895 8.7900 8.7904 8.7910 |
B = 8.9846
-0.0618
b1 = 8.9846
b2 = -0.0618
y=8.98-0.06x
m-, ( ).
3.3
(F- )
.
F=S12/S22
F F
=1-
–
F?F, ( ) ( ).
R – , .
iyi- c
–
F1 – ,
n –
i- . i
yi –
– . . , .
F?F, , .
.
. .
:
:
Pras1 = 6563.6; Pras2 = 6563.6; Pras3 = 6563.6; Pras4 = 6563.6; Pras5 = 6563.6; Pras6 = 6563.6; Pras7 = 6563.5; Pras8 = 6563.5; Pras9 = 6563.5; Pras10 = 6563.5
Sost2 = 105.5628
:
Pras1 = 6.543.0; Pras2 = 6546.7; Pras3 = 6549.0; Pras4 = 6552.4; Pras5 = 6554.6; Pras6 = 6556.7; Pras7 = 6570.4; Pras8 = 6574.0; Pras9 = 6575.8; Pras10 = 6578.4
Sost2 = 0.4071;
:
Pras1 = 6545.8; Pras2 = 6549.8; Pras3 = 6552.2; Pras4 = 6556.7; Pras5 = 6559.8; Pras6 = 6562.7; Pras7 = 6.65.4; Pras8 = 6568.1; Pras9 = 6.5706; Pras10 = 6573.9 Sost2 = 0.6517
m-, F- ( ).
– . , .
1 , , , . , ( 2). , 2.1, , , , LAB. 2.2 , . 2.3 : (4-5) , – . m-, . 3 . . 3.1- . 3.2- (m- ).
.
1. .. .. : . . .: . ., 2004. 390 .
2. .. .., .. : . .-5- ., . .: , 2004. 560 .
3. . .: , 2001. 300 .
4. .. MATLAB 7.. .: , 2006. 256 .
5. https://www.exponenta.ru.
6. https://www.diarea.ru.
7. https://www.med2000.ru.
1
2
https://www.allbest.ru/
m-, :
Pa=6650%
Po=127%
pi=3.14
ksy=0.5%
f=1.2
w=2*pi*f%
E=0.9%
h=0.16%
ro=600%
d=4.77%
t=0:pi/50:1*pi%
x=0.22%
v=sqrt(E*h/ro*d)%
P=Pa+Po*exp(-ksy*x)*(cos(w*(t-x/v)))%
grid on
plot(t,P)
[3,4]
m-, :
P1=6552
P2=6555
P3=6557
P4=6561
P5=6563
P6=6566
P7=6570
P8=6573
P9=6575
P10=6578
t1=((acos((P1-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t2=((acos((P2-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t3=((acos((P3-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t4=((acos((P4-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t5=((acos((P5-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t6=((acos((P6-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t7=((acos((P7-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t8=((acos((P8-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t9=((acos((P9-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t10=((acos((P10-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
T=[t1 t2 t3 t4 t5 t6 t7 t8 t9 10]’
ed=[1 1 1 1 1 1 1 1 1 1]’
X=[ed T]
Y=[log(P1) log(P2) log(P3) log(P4) log(P5) log(P6) log(P7) log(P8) log(P9) log(P10)]’
B=((X’*X)^(-1))*X’*Y
b1=B(1)
b2=B(2)
m-, :
P1=6544
P2=6547
P3=6549
P4=6552
P5=6554
P6=6556
P7=6570
P8=6574
P9=6576
P10=6579
t1=((acos((P1-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t2=((acos((P2-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t3=((acos((P3-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t4=((acos((P4-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t5=((acos((P5-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t6=((acos((P6-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t7=((acos((P7-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t8=((acos((P8-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t9=((acos((P9-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t10=((acos((P10-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
T=[t1 t2 t3 t4 t5 t6 t7 t8 t9 t10]’
ed=[1 1 1 1 1 1 1 1 1 1]’
X=[ed T]
Y=[log(P1) log(P2) log(P3) log(P4) log(P5) log(P6) log(P7) log(P8) log(P9) log(P10)]’
B=((X’*X)^(-1))*X’*Y
b1=B(1)
b2=B(2)
m-, :
P1=6547
P2=6550
P3=6552
P4=6556
P5=6559
P6=6562
P7=6565
P8=6568
P9=6571
P10=6575
t1=((acos((P1-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t2=((acos((P2-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t3=((acos((P3-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t4=((acos((P4-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t5=((acos((P5-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t6=((acos((P6-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t7=((acos((P7-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t8=((acos((P8-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t9=((acos((P9-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
t10=((acos((P10-Pa)/(Po*exp(-ksy*x))))/w)+(x/v)
T=[t1 t2 t3 t4 t5 t6 t7 t8 t9 t10]’
ed=[1 1 1 1 1 1 1 1 1 1]’
X=[ed T]
Y=[log(P1) log(P2) log(P3) log(P4) log(P5) log(P6) log(P7) log(P8) log(P9) log(P10)]’
B=((X’*X)^(-1))*X’*Y
b1=B(1)
b2=B(2)
m- F-:
Pras1=exp(b1+b2*t1)
Pras2=exp(b1+b2*t2)
Pras3=exp(b1+b2*t3)
Pras4=exp(b1+b2*t4)
Pras5=exp(b1+b2*t5)
Pras6=exp(b1+b2*t6)
Pras7=exp(b1+b2*t7)
Pras8=exp(b1+b2*t8)
Pras9=exp(b1+b2*t9)
Pras10=exp(b1+b2*t10)
Sost2=((Pras1-P1)^2+(Pras2-P2)^2+(Pras3-P3)^2+(Pras4-P4)^2+(Pras5-P5)^2+(Pras6-P6)^2+(Pras7-P7)^2+(Pras8-P8)^2+(Pras9-P9)^2+(Pras10-P10)^2)/(10-2-1)
Allbest.ru
…
Источник
14
БИОФИЗИКА СИСТЕМЫ КРОВООБРАЩЕНИЯ.
Для описания процессов, происходящих в системе кровообращения, применяются методы физического, аналогового и математического моделирования.
Гемодинамические показатели кровотока определяются собственными характеристиками сердечной деятельности (например ударным объемом крови), структурными особенностями сосудов (их радиусом и эластичностью) и свойствами самой крови (вязкостью).
Реологические свойства крови
Реология (от греч. rheos- течение, поток, logos- учение) – это наука о деформациях и текучести вещества. Под реологией крови (гемореологией) будем понимать изучение биофизических особенностей крови как вязкой жидкости.
Вязкость (внутреннее трение) жидкости – свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. Вязкость жидкости обусловлена, межмолекулярным взаимодействием. Наличие вязкости приводит к диссипации энергии внешнего источника, вызывающего движение жидкости, и переходу ее в теплоту.
Основной закон вязкого течения был установлен И. Ньютоном:
(15.1)
где F [H] – сила внутреннего трения (вязкости), возникающая между слоями жидкости при сдвиге их относительно друг друга;
[Па-с] – коэффициент динамической вязкости жидкости, характеризующий сопротивление жидкости смещению ее слоев;
[1/с] – градиент скорости, показывающий, на сколько изменяется скорость V при изменении на единицу расстояния в направлении Z при переходе от слоя к слою;
S- площадь соприкасающихся слоев .
Наряду с коэффициентом динамической вязкости рассматривают так называемый коэффициент кинематической вязкости (плотность жидкости).
Жидкости делятся по вязким свойствам на два вида: ньютоновские и неньютоновские.
Ньютоновской называется жидкость, коэффициент вязкости которой зависит только от её природы и температуры. Для ньютоновских жидкостей сила вязкости прямо пропорциональна градиенту скорости . Для них непосредственно справедлива формула Ньютона (15.1), коэффициент вязкости в которой является постоянным параметром.
Неньютоновской называется жидкость, коэффициент вязкости которой зависит не только от природы вещества и температуры, но также и от условий течения жидкости, в частности от градиента скорости. Коэффициент вязкости в этом случае не является константой вещества. Зависимость силы вязкости от градиента скорости становится нелинейной:
(15.1а)
где n характеризует механические свойства вещества при данных условиях течения. Примером неньютоновских жидкостей являются суспензии. Если имеется жидкость, в которой равномерно распределены твердые невзаимодействующие частицы, то такую среду можно рассматривать как однородную, если мы интересуемся явлениями, характеризующимися расстояниями, большими по сравнению с размером частиц. Свойства такой среды в первую очередь зависят от жидкости. Для случая малых концентраций частиц С справедлива формула : (15.2)
где К геометрический фактор – коэффициент, зависящий от геометрии частиц (их формы, размеров), для сферических частиц К вычисляется по формуле:
(15.2а)
(R – радиус шара). Для эллипсоидов К увеличивается и определяется значениями его полуосей и их соотношениями. Если структура частиц изменится (например, при изменении условий течения), то и коэффициент К в (15.2), а следовательно и вязкость такой суспензии также изменится. Подобная суспензия представляет собой неньютоновскую жидкость. Увеличение вязкости всей системы связано с тем, что работа внешней силы при течении суспензий затрачивается не только на преодоление вязкости, обусловленной межмолекулярным взаимодействием в жидкости, но и на преодоление взаимодействия между ней и структурными элементами.
Кровь – неиьютоновская жидкость, т.к. она обладает внутренней структурой, где 93% форменных элементов составляют эритроциты, и при упрощенном рассмотрении кровь – это суспензия эритроцитов в физиологическом растворе. Характерным свойством эритроцитов является тенденция к образованию агрегатов. Если нанести мазок крови на предметный столик микроскопа, то можно видеть, как эритроциты “склеиваются” друг с другом, образуя агрегаты, которые получили название монетных столбиков. Условия образования агрегатов различны в крупных и мелких сосудах. Это связано в первую очередь с соотношением размеров сосуда, агрегата и эритроцита (характерные размеры: dэр8 мкм, darp10 d3p).
Здесь возможны три варианта. 1. Крупные сосуды {аорта, артерии):
При этомградиент dV/dZ небольшой, эритроциты собираются в агрегаты в виде монетных столбиков. В этом случае вязкость крови= 0,005 Па-с.
2. Мелкие сосуды {мелкие артерии, артериолы):
В них градиент dV/dZ значительно увеличивается и агрегаты распадаются на отдельные эритроциты, тем самым уменьшая вязкость системы. Для этих сосудов чем меньше диаметр просвета, тем меньше вязкость крови. В сосудах диаметром около 5 d3p вязкость крови составляет примерно 2/3 вязкости крови в крупных сосудах.
3. Микрососуды {капилляры):
Наблюдаетсяобратный эффект: с уменьшением просвета сосуда вязкость возрастает в 10-100 раз. В живом сосуде эритроциты легко деформируются и проходят, не разрушаясь, через капилляры даже диаметром 3 мкм. При этом они сильно деформируются, становясь похожими на купол. В результате поверхность соприкосновения эритроцитов со стенкой капилляра увеличивается по сравнению с недеформированным эритроцитом, способствуя обменным процессам.
Таким образом, внутренняя структура крови, а следовательно и ее вязкость (15.2), оказывается неодинаковой в зависимости от условий течения вдоль кровеносного русла, поэтому кровь – неньютоновская жидкость. Зависимость силы вязкости от градиента скорости для течения крови по сосудам является нелинейной.
Вязкость, характерная для течения крови в крупных сосудах: в норме;при анемии, при
полицитемии . Вязкость плазмы
Вязкость воды
Как и у любой жидкости, вязкость крови возрастает при снижении температуры. Например, при уменьшении температуры с 37до 17вязкость крови возрастает на 10%.
Режимы течения крови
Режимы течения жидкости разделяют на ламинарное и турбулентное. Ламинарное течение- это упорядоченное течение жидкости, при котором она перемещается как бы слоями, параллельными направлению течения. С увеличением скорости движения ламинарное течение в некоторый момент внезапно переходит в турбулентное течение, при котором происходит интенсивное перемешивание между слоями жидкости, в потоке возникают многочисленные вихри различных размеров. При этом изменяются свойства течения, в частности структура потока, профиль скоростей (рис. 15.1), закон сопротивления.
Режим течения жидкостихарактеризуется числом Рейнольдса Re. Для течения жидкости в круглой цилиндрической трубе:

Рис. 15.1. Профиль скоростей при ламинарном (а) и турбулентном (б; течениях
(15.3)
где V – скорость течения, средняя по поперечному сечению, R радиус трубы.
Когда значение Re меньше критического, имеет место ламинарное течение жидкости, если, то течение становится турбулентным. Как правило, движение крови по сосудам является ламинарным.
Однако в ряде случаев возможно возникновение турбулентности. Турбулентное движение крови в аорте может быть вызвано турбулентностью кровотока у входа в нее: вихри потока уже изначально существуют, когда кровь выталкивается из желудочка в аорту, что хорошо наблюдается при доплер кардиографии. У мест разветвления сосудов, а также при возрастании скорости кровотока (например, при мышечной работе) течение может стать турбулентным и в артериях.
Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, поэтому в кровеносной системе это может привести к дополнительной нагрузке на сердце.
Гемодинамика- один из разделов биомеханики, изучающий законы движения крови по кровеносным сосудам. Задача гемодинамики – установить взаимосвязь между основными гемодинамическими показателями, а также их зависимость от физических параметров крови и кровеносных сосудов.
К основным гемодинамическим показателям относятся давление и скорость кровотока.
Давление – это сила, действующая со стороны крови на сосуды, приходящаяся на единицу площади: Р = F / S.
Скорость кровотока: различают объемную и линейную. Объемной скоростью называют объем жидкости, протекающей в единицу времени через данное сечение трубы= v/t , единица измерения – . Линейная скорость представляет путь, проходимый частицами крови в единицу времени V = 1/t, единица измерения – [м/с]. Поскольку линейная скорость неодинакова по сечению трубы, то в дальнейшем речь будет идти только о линейной скорости, средней по сечению . Линейная и объемная скорости связаны простым соотношением, где S площадь поперечного сечения потока жидкости.
Так как жидкость несжимаема (то есть плотность ее всюду одинакова), то через любое сечение трубы и в единицу времени протекают одинаковые объемы жидкости:
(9.4)
Это называется условием неразрывности струи. Оно вытекает из закона сохранения массы для несжимаемой жидкости. Уравнение неразрывности струи относится в равной мере к движению всякой жидкости, в том числе и вязкой. При описании физических законов течения крови по сосудам вводится допущение, что количество циркулирующей крови в организме постоянно. Отсюда следует, что объемная скорость кровотока в любом сечении сосудистой системы также постоянна:
В реальных жидкостях (вязких) по мере движения их по трубе потенциальная энергия расходуется на работу по преодолению внутреннего трения, поэтому давление жидкости вдоль трубы падает. Для стационарного ламинарного течения реальной жидкости в цилиндрической трубе постоянного сечения справедлива формула (закон) Гагена – Пуазейля:
(9.5)
где- падение давления, то есть разность давлений у входа в трубуи на выходе из нее на расстоянии 1. (Данная закономерность была эмпирически установлена учеными Гагеном (1839 г.) и Пуазейлем (1840 г.) независимо друг от друга. Часто носит название закон Пуазейля.) Величина
(9.6)
называется гидравлическим сопротивлением сосуда. Выражение (9.5) можно представить как
(9.5а)
Из закона Пуазейля (9.5) следует, что падение давления крови в сосудах зависит от объемной скорости кровотока и в сильной степени от радиуса сосуда. Так уменьшение радиуса на 20% приводит к увеличению падения давления более чем в 2 раза. Даже небольшие изменения просветов кровеносных сосудов сильно сказываются на падении давления. Не случайно основные фармакологические средства нормализации давления направлены прежде всего на изменение просвета сосудов.
Границы применимости закона Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4)удаленное расстояние от источников возмущений (от входа, изгибов, сужений).
Гемодинамические показатели в разных частях сосудистой системы
Гидравлическое сопротивление
Гидравлическое сопротивление w в значительной степени зависит от радиуса сосуда (9.6). Отношения радиусов для различных участков сосудистого русла:
Поскольку гидравлическое сопротивление в сильной степени зависит от радиуса сосуда: , то можно записать соотношение:
Линейная скорость кровотока
Рассмотрим закон неразрывности (9.4). Площадь суммарного просвета всех капилляров в 500-600 раз больше поперечного сечения аорты. Это означает, что. Именно в капиллярной сети при медленной скоростидвижения происходит обмен веществ между кровью и тканями.
На рис. 9.2 приведена кривая распределения линейных скоростей вдоль сосудистой системы.

Рис. 9.2. Линейная скорость в различных участках сосудистого русла
Распределение среднего давления
При сокращении сердца давление крови в аорте испытывает колебания (см. п. 9.3). Падение среднего давления крови за период вдоль сосудов может быть описано законом Пуазейля (9.5а). Сердце выбрасывает кровь под средним давлением Роср . По мере продвижения крови по сосудам среднее давление падает. Поскольку, а , то для средних значений давления:
На протяжении крупных сосудов среднее давление падает всего на 15%, а в мелких на 85%. Это означает, что большая часть энергии, затрачиваемой левым желудочком сердца на изгнание крови, расходуется на ее течение по мелким сосудам.
Распределение давления (превышение над атмосферным) в различных отделах сосудистого русла представлено на рис. 9.3. Отрицательное значение давления означает, что оно несколько ниже атмосферного

Рис. 9.3. Распределение давления (превышение над атмосферным) в различных участках сосудистого русла (штриховкой обозначено область колебания давления в систолу и диастолу, пунктиром – среднее давление), 1 – давление в аорте, 2 – в крупных артериях, 3 – в мелких артериях, 4 – в артериолах, 5 – в капиллярах
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
