Модуль упругости стенки сосуда
Стенка всех кровеносных сосудов, за исключением капилляров, построена из вязкоэластического материала. Поэтому крупные сосуды способны к значительным обратимым изменениям размера при действии на их стенку внешней деформирующей силы, а также при активном сокращении и расслаблении гладкой мускулатуры самой стенки.
Для выяснения общих механических свойств сосудистой стенки и их изменения при патологических состояниях изучают ее изолированные полоски; при этом определяют кривые растяжения (см. рис. 83) при тангенциальной (по направлению окружности поперечного сечения) или продольной (вдоль длинной оси сосуда) деформации под действием соответственно сил f01 и f. Статические кривые растяжения сосудистой стенки (рис. 82) подобны соответствующим характеристикам деформации скелетной мышцы (см. рис.78).
Наибольший интерес представляет деформация целого сосуда. Ее обычно наблюдают в условиях, когда деформирующая сила создается внутренним избыточным давлением р. При варьировании р в основном изменяется просвет (площадь поперечного сечения) сосуда, а длину можно считать постоянной величиной. Такое явление происходит в организме в естественных условиях течения крови по кровеносным сосудам и играет большую роль в гемодинамических процессах (см. гл. 12). Найдем количественную связь между параметрами кровеносного сосуда и внутренним давлением.
Примем, что сосуд имеет цилиндрическую форму. Рассмотрим сегмент такого сосуда длиной l с внутренним радиусом поперечного сечения г и толщиной стенки h (рис. 83). Плоскостью, проходящей через диаметр, условно разделим сосуд в продольном направлении на две половины. Образовавшееся внутреннее сечение имеет площадь. На эту площадку действует сила f, обусловленная давлением: f = р ? 2rl. Сила f стремится разъединить две половины сосуда, в результате чего в сосудистой стенке появляются упругие силы, направленные тангенциально (по касательной) к окружности поперечного сечения и перпендикулярно площадкам продольного сечения стенки. Суммарная тангенциальная упругая сила ft , очевидно, определяется выражением ft = ут ? 2hl, где ут – тангенциальное напряжение в стенке; 2hl – сумма площадей продольных сечений стенки, к которым приложена fт.
Силы f и fт уравновешивают друг друга, так что
Это выражение носит название уравнения Ламе. Оно описывает равновесное состояние сосуда при данном давлении р.
В общем случае при сдвиге р изменяются и r и h. Однако можно считать, что объем стенки, равный 2рrhl при r ?h, представляет собой неизменную величину, поскольку l = const, произведение rh тоже можно принять в качестве неизменного параметра. Тогда уравнение Ламе можно записать в виде
где a = rh и не зависит от р и r. Проанализируем теперь состояние сосуда после изменения давления на dp, которому соответствуют изменения тангенциального напряжения на d ут и радиуса на dr. В этом состоянии давление, напряжение и радиус равны соответственно (р + dp), (ут+ dут) и (r + dr) и, согласно соотношению Ламе,
Раскрывая скобки в правой части этого уравнения и пренебрегая членами, содержащими dpdr или (dr)2, получаем
Вычитая (10.10) из (10.12), имеем
В этом выражении dут – это то тангенциальное напряжение, которому соответствует изменение длины стенки по окружности на 2р(r + dr) – 2рr. По закону Гука
где Е – эффективный модуль упругости сосудистой стенки. При объединении уравнений (10.14) и (10.13) получается, что
Это выражение легко преобразовать в зависимость изменения просвета сосуда от dp. Исходная величина просвета s равна рr2, его изменение ds = d(рr2) = 2рrdr. Отсюда dr = ds/2рr, и подстановка этого соотношения в (10.15) дает:
Выражения (10.15) и (10.16) – основные уравнения деформации кровеносного сосуда: расширения при увеличении давления на dp или сужения при уменьшении давления на dp.
При высоком модуле упругости сосудистой стенки часто оказывается, что второй член в скобках в уравнениях (10.15) и (10.16) гораздо меньше первого члена и им можно пренебречь. Тогда уравнения деформации принимают более простой вид:
Эти выражения широко используются при описании течения крови, распространения пульса по кровеносным сосудам (см. гл. 12). Уравнения (10.15) и (10.16), а также (10.17) и (10.18) применяются для расчета эффективного модуля упругости сосудистой стенки, характеризующего тангенциальную деформацию. Для этого, как видно из указанных выражений, в эксперименте необходимо измерить давление внутри сосуда, его радиус, толщину стенки и изменение давления и радиуса.
Деформация сосудов артериальной части системы кровообращения протекает в организме в динамических условиях: подъем давления и последующий его спад совершаются за непродолжительное время. В этих условиях, как говорится на с. 197, модуль упругости зависит от времени и всегда выше модуля упругости, рассчитанного для состояния равновесия [см. уравнение (10.7)]. Для определения зависящего от времени динамического модуля упругости используются два метода. При первом методе искусственно вызывают периодическое изменение радиуса путем циклического механического сжатия сосуда и измеряют dp и dr, а затем рассчитывают модуль упругости по уравнению типа (10.15). В зависимости от частоты деформации динамический модуль упругости отражает упругие свойства стенки в разные моменты времени после начала деформации. Скажем, при частоте 5Гц это время равно примерно 0,1 с.
Другой способ косвенный. Он состоит в измерении скорости распространения по сосуду волны давления (см. гл. 12, уравнение 12.18). На рис. 84 в качестве примера показана зависимость модуля упругости нижней полой вены собаки от напряжения ут при исследовании в эксперименте in situ.
Оказалось, что динамический модуль упругости резко возрастает при увеличении напряжения в сосудистой стенке (давления внутри сосуда) и, что особенно важно, может по крайней мере на порядок превосходить статический модуль упругости (см. рис. 84). Аналогичная картина наблюдается на артериях человека. Например, динамический модуль упругости (определяемый первым способом при частоте деформации 10 Гц) восходящей дуги аорты может составлять в зависимости от возраста 106 – 3? 106Н/м2, а статический – всего около 5 ? 104 Н/м2. Совершенно ясно, что быстропротекающие процессы деформации кровеносных сосудов в организме необходимо описывать динамическим, а не статическим модулем упругости.
Источник
Эластиновые нити обладают сравнительно высокой растяжимостью, т. е. низким модулем упругости при растяжении вдоль волокна (0,4—1,0) 10 Н/м . Коллагено-вые нити имеют на порядок более высокий модуль упругости (0,5—1,0) 10 Н/м , т. е. характеризуются более низкой способностью к растяжению. Считают, что в тканях волокна эластина находятся под напряжением уже при умеренном растяжении. Коллагеновые волокна сами по себе оказываются в состоянии натяжения лишь при сильной деформации тканей Обладая высоким модулем упругости и прочностью, эти волокна предотвращают разрыв сухожилий, стенок кровеносных сосудов и других тканей при больших механических нагрузках, а в легких обеспечивают тканевую стабилизацию альвеол при больших объемах. При слабой деформации тканей нити коллагена не растянуты, но при этом деформируется их сеть. [c.211]
Существует много других подтверждений правильности линейной модели кровотока. Например, согласно уравнению (12.18), скорость распространения волны давления по крупным сосудам должна возрастать с увеличением модуля упругости сосудистой стенки Е. Это подтверждается опытом. Известно, что у человека Е увеличивается с возрастом. Соответственно этому скорость распространения пульсовой волны у пожилых выше, чем в молодом возрасте. Впрочем, известны и отклонения от линейной теории, связанные с тем, что сосудистая стенка не является идеально упругим материалом, а обладает также и вязкостным свойством. [c.236]
Эти выражения широко используются при описании течения крови, распространения пульса по кровеносным сосудам (см. гл. 12). Уравнения (10.15) и (10.16), а также (10.17) и (10.18) применяются для расчета эф( №ктивного модуля упругости сосудистой стенки, характеризующего тангенциальную деформацию. Для этого, как видно из указанных выражений, в эксперименте необходимо измерить давление внутри сосуда, его радиус, толщину стенки и изменение давления и радиуса. [c.204]
При плавлении твердого тела происходит скачок в величине текучести. Наличие этого свойства не является качественным отличием жидкости от твердого тела, так как последнее обладает ползучестью. Вместе с тем механизм ползучести совершенно отличен от механизма текучести. Наличие упругости у твердого тела ие является его качественным отличием от жидкости. Жидкость также можно упруго расширять и сжимать. Од1 ако измерению подобных явлений изменений препятствует текучесть жидкости. Если, однако, тщательно заполнить жидкостью некоторый, предварительно откачанный сосуд, а затем охладить его, то жидкость не оторвется от стенок из-за уменьшения объема и окажется растянутой. Такнм путем измеряли модуль упругости жидкости. Потеря дальнего порядка при плавлении определяет скачкообразное изменение свойств жидкости. Объяснение скачкообразности переходов является одной пз задач теории жидкого состояния. Основным отличием жидкости от газа является наличие границы между жидкого [c.207]
Строго говоря, величины параметров ц, Е к тем более 5 и г в уравнениях (12.5) и (12.9) могут изменяться при сдвиге давления в сосуде. Однако при высоких скоростях кровотока, характерных для магистральных сосудов, вязкость крови можно считать постоянной величиной (см. раздел 12.1). При быстрых изменениях давления, характерных для пульса, величина эффективного модуля упругости стенки кровеносных сосудов Е достигает высоких величин (см. гл. 10) и, следовательно, 5 изменяется незначительно. Наконец, сам модуль Е можно считать постоянной величиной при небольших изменениях 5. Таким образом, можно принять за постоянные величины все параметры сосуда и крови, стоящие перед производными в выражениях (12.5) и (12.9). Введем новые постоянные [c.231]
Е — модуль упругости первого рода, кГ мм (при температуре стенки сосуда) [c.99]
В этих формулах приняты следующие обозначения а — коэффициент удлинения Е — модуль упругости в кГ/см -, в—температура внутренней стенки сосуда в °С н — температура наружной стенки сосуда в °С гп — коэф- [c.147]
Для сосудов н аппаратов, работающих под наружным избыточным давлением, гидравлическое давление допускается определять как Рпр = = 1,25Я( 2о/ ), если значения 1,25 Р( [ff]2o/[ r]) или 0,2 МПа вызывают необходимость утолщения стенки аппарата ( 20 — модуль упругости при 20 °С Е — модуль упругости при расчетной температуре). [c.373]
Сохраняя методику определения толщин стенок сосудов и аппаратов, работающих под давлением и с коэффициентами линейного расширения обоих слоев Oj я Oj, и модулями упругости Е2, необходимо за расчетную толщину принимать суммарную толщину обоих слоев, т. е. толщину s = + s . [c.175]
Ей Ег, Vl2, У21 — модули упругости и коэффициенты поперечной деформации в осевом и окружном направлениях, Ri — радиус срединной поверхности сосуда, соответствующий /-му значению ро к — толщина стенки. [c.133]
Расчетную схему аневризмы построим при следующих допущениях 1) материал аневризмы однородный изотропный 2) купол аневризмы осесимметричен (рис. 3.23, а), а стенка аневризмы однослойная с конструктивным модулем упругости Еу”, 3) основание аневризмы жестко закреплено в сосуде 4) геометрические размеры аневризмы и внутреннее давление в ней рассматриваются в физиологическом диапазоне. [c.137]
Если растянутая макромолекула закреплена, как показано на рис. 4.16, то на точки закрепления вследствие теплового движения и перехода от одних конформаций к другим будут действовать различные мгновенные силы (по модулю и направлению), стремящиеся в целом стянуть концы макромолекулы -(аналогично тому, как действуют на стенку сосуда удары молекул газа, летящих с различными скоростями в разных направлениях, но в целом приводящие к возникновению нормальной силы или давления газа). В результате на концах макромолекулы действуют средние значения упругих сил, приложенных к прямой, соединяющей оба конца, и стремящихся стянуть эти концы. Так как концы закреплены, то на них возникают реакции, т. е. внешние силы , направленные противоположно упругим силам макромолекулы. Таким образом, векторы Т и Ь коллинеарны. [c.103]
Деформация сосудов артериальной части системы кровообращения протекает в организме в динамических условиях подъем давления и последующий его спад совершаются за непродолжительное время. В этих условиях, как говорится на с. 197, модуль упругости зависит от времени и всегда выше модуля упругости, рассчитанного для состояния равновесия (см. уравнение (10.7)]. Для определения зависящего от времени динамического модуля упругости используются два метода. При первом методе искусственно вызывают периодическое изменение радиуса путем циклического механического сжатия сосуда и измеряют йр и йг, а затем рассчитывают модуль упругости по уравнению типа (10.15). В зависимости от частоты деформации динамический модуль упругости отражает упругие свойства стенки в разные моменты времени после начала деформации. Скажем, при частоте 5Гц это время равно примерно 0,1 с. [c.204]
Выводы линейной теории кровотока по упругим сосудам тем не менее могут использоваться для изучения ряда характеристик системы кровообращения. Например, измеряя скорость распространения пульса, можно определить модуль упругости сосудистой стенки Е по уравнению (12.18). Измеряя давление в двух близко расположенных участках сосуда и зная / и можно рассчитывать по уравнению (12.11) импульс объемного расхода крови. [c.236]
Здесь S — толщина стенки оболочки, м Епр =У н/м — приведенный модуль упругости биметалла D — внутренний диаметр сосуда, ж I — расчетная длина обечайки, ж Рр — рабочее давление, н1мР- [р] — допускаемое давление н1м С Со i — поправки, учитывающие коррозию, округление расчетной толщины листа и способ изготовления аппарата. [c.137]
Здесь / — момент инерции кольца жесткости относительно оси, проходящей через центр тяжести его поперечного сечения и параллельной образующей цилиндрического корпуса, в см можно принимать, что с приваренным кольцом жесткости работает совместно и часть стенки сосуда или аппарата протяженностью по 4—8 толщин стенки на сторону от приварного элемента К — радиус по центру тяжести поперечного сечения кольца жесткости в см для предварительных расчетов К принимают равным внутреннему радиусу цилиндрического корпуса в см Е — модуль упругости материала в кПсм . [c.360]
Источник
Лекция 4. Реологические свойства биологических об ъектов. Гемодинамика • Биологические жидкости и их характеристики • Уравнение Ньютона. Вязкость жидкостей. • Ньютоновские и неньютоновские жидкости • Вязкость крови и методы ее измерения • Характер течения жидкости. Число Рейнольдса • Объемная скорость течения. Уравнение Пуазейля. Гидравлическое сопротивление сосудов
Биореология. Вязкость. • Биореология – наука о деформациях и текучести жидких сред организма. • При течении жидкостей отдельные ее слои взаимодействуют между собою с силами, направленными по касательным к слоям. Это явление называют вязкостью ( ).
Физический смысл вязкости • Физический смысл вязкости находят из уравнения Ньютона. • Вязкостью называют силу, действующую на единицу площади слоев жидкости при градиенте их скоростей равном единице
Ньютоновские и неньютоновские жидкости • Ньютоновскими называют жидкости, коэффициент вязкости которых зависит только от их природы и температуры. • Неньютоновскими называют жидкости, коэффициент вязкости которых зависит не только от природы вещества и температуры, но также и от условий течения жидкости, в частности от градиента скорости.
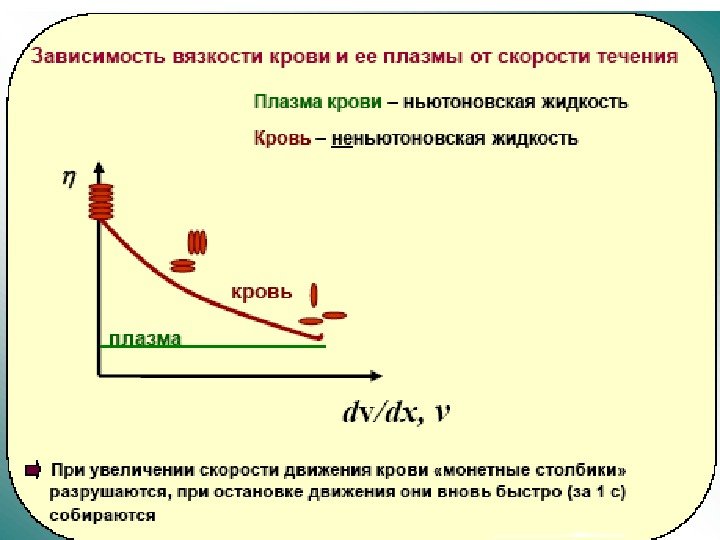
Методы измерения вязкости крови • Совокупность методов измерения вязкости жидкости называется вискозиметрией. Прибор для измерения вязкости называется вискозиметром. В зависимости от метода измерения вязкости используют следующие типы вискозиметров.
Метод Стокса Вискозиметр Гесса Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость помещается в малый зазор между двумя телами, необходимый для сдвига исследуемой среды.
Уравнение неразрывности • Условие неразрывности струи: при стационарном течении несжимаемой жидкости через любые сечения трубки тока каждую секунду протекают одинаковые объемы жидкости, равные произведению площади сечения на среднюю скорость движения ее частиц. • Q 1 =Q 2 =Q 3 =(Sn vn )=…=const • v 2 =(S 1 v 1 )/S 2 =(r 1 /r 2 ) 2 ∙ v 1 =(d 1 /d 2 ) 2 ∙ v
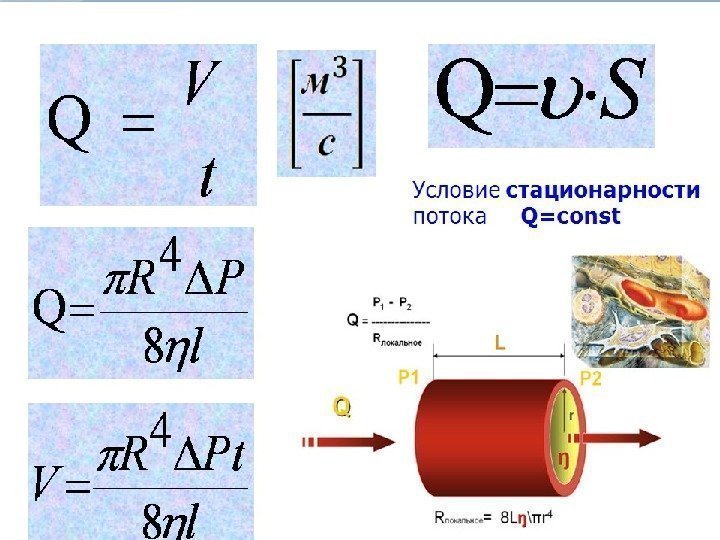
• Гемодинамика – раздел биомеханики, который изучает законы движения крови по сосудам. • Основной причиной движения крови по сосудам является разность давлений в начале и конце сосудистого русла. • Разность давлений обеспечивает такой важный гемодинамический параметр как объемная скорость кровотока.
Основные положения гемодинамики Основной причиной движения крови по сосудам является разность давлений в начале и конце сосудистого русла, которая определяет такой гемодинамический параметр, как объемная скорость кровотока ( Q ): l Pr X P Q
Работа и мощность сердца • Работа, совершаемая сердцем, затрачивается на преодоление сил давления и сообщение крови кинетической энергии. Рассчитаем работу, совершаемую при однократном сокращении левого желудочка. Изобразим V y д — ударный объем крови — в виде цилиндра. Можно считать, что сердце продавливает этот объем по аорте сечением S на расстояние I при среднем давлении р. Так как работа правого желудочка принимается равной 0, 2 от работы левого, то работа всего сердца при однократном сокращении равна:
• Ударным объемом Vуд называют объем крови, который выталкивается из левого желудочка в аорту во время систолы. В норме его величина составляет 60 мл = 6∙ 10 -6 м 3 • Среднее давление в норме 13 10 3 Па, средняя скорость движения крови в аорте составляет 0, 5 м/с. При ЧСС= 60 уд/мин за одно сокращение сердце выполняет работу в 1 Дж, а мощность сердца равна 3, 3 Вт Работа и мощность сердца
Измерение артериального давления • Одним из основных гемодинамических показателей является артериальное давление. • Давление — это сила, действующая со стороны крови на сосуды, приходящаяся на единицу площади: Р= F / S • Максимальное Р с и минимальное Р д давление находят при помощи метода Короткова или осцилляторным методом. Среднее давление крови находят по формуле:
Среднее артериальное давление 3 dc dpc PP PP
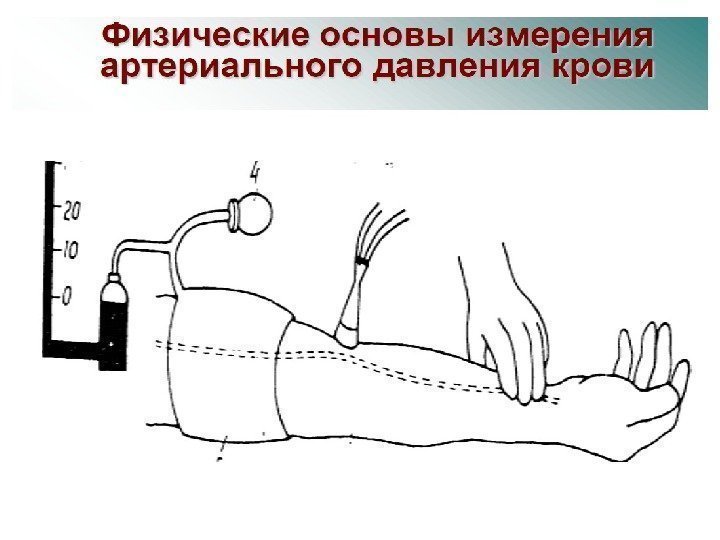
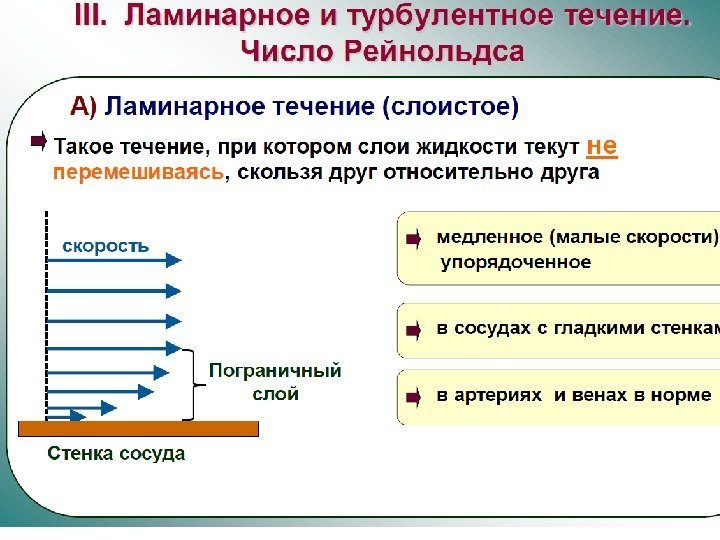
Клинический метод измерения АД • Клинический метод измерения АД основан на регистрации систолического давления по появлению звука, вызванного турбулентным течением крови через сдавленную артерию и диастолического давления по исчезновению звука, вызванного переходом течения крови от турбулентного к ламинарному.
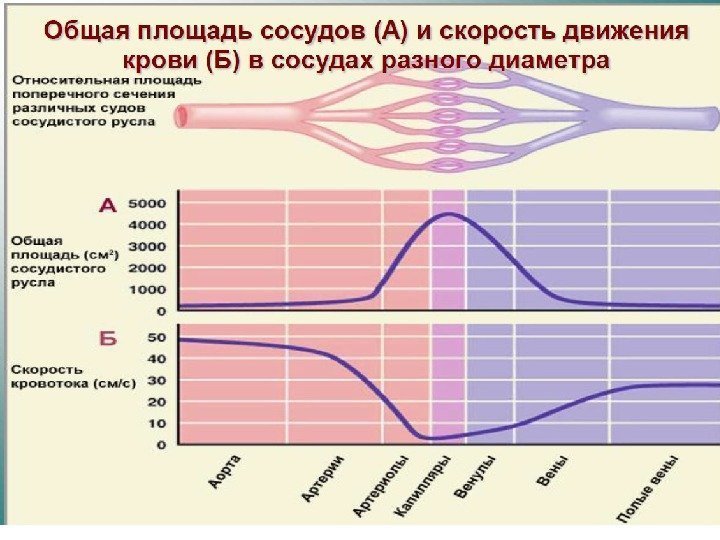
Физическая функция каждого элемента сердечно-сосудистой системы • Основная функция сердечно-сосудистой системы — обеспечение непрерывного движения крови по капиллярам, где происходит обмен веществ между кровью и тканями. Артериолы — резистивные сосуды. Легко изменяя свой просвет, они регулируют гемодинамические показатели кровотока в капиллярах. Артериолы — «краны» сердечно-сосудистой системы.
• Сердечно-сосудистая система замкнута, поэтому для обеспечения течения крови в ней должен быть периодически действующий насос. Эту роль выполняет сердце. Периодическое поступление крови из сердца превращается в постоянное поступление ее в мелкие сосуды с помощью крупных сосудов: часть крови, поступающей из сердца во время систолы, резервируется в крупных сосудах благодаря их эластичности, а затем во время диастолы выталкивается в мелкие сосуды.
• Крупные сосуды являются согласующим элементом между сердцем и мелкими сосудами. При этом аорта и артерии выполняют роль проводников, позволяя подводить кровь к различным частям тела. По венам кровь возвращается в сердце.
Механические характеристики сосудов • Прохождение крови по сосудам вызывает их деформацию ─ изменение размеров или формы тела под действием внешней нагрузки. . . Упругая деформация ─ деформация, которая исчезает после снятия внешней нагрузки (т. е. тело полностью восстанавливает форму и размеры). • Пластическая деформация ─ деформация, которая не исчезает после снятия внешней нагрузки (т. е. тело не восстанавливает форму и размеры).
Закон Гука • Упругие деформации в теле подчиняются закону Гука ( закону упругих деформаций ): механическое напряжение ( = F/S ) , возникающее в теле при его деформации, прямо пропорционально величине его относительной деформации ( ) : • = E; • где: = l/l 0 = (l — l 0 )/l 0 – относительная деформация; E – модуль упругости (модуль Юнга)
Уравнение Лапласа • Т= (Р вн — Р нар ) r/h • Где Т- тонус сосуда; • Р вн — внутреннее давление; • Р нар — наружное давление; • r – радиус сосуда; • h – толщина стенки сосуда
Пульсовая волна Пульсовой волной называют волну повышенного давления, вызванную выбросом крови из левого желудочка в период систолы и распространяющуюся по аорте и артериям.
• Задача 1. • Скорость пульсовой волны в артериях составляет 10 м/с. Чему равен модуль упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки сосуда равна 8, а плотность крови равна 1, 05∙ 10 3 кг/м 3 .
• Решение. • v= E h/(2 ∙r). Следовательно: • E h=2 ∙r∙v 2 , откуда: • E =(2 ∙r∙v 2 )/h • Проверка размерности: • [ Па ] =[ кг ∙ м 2 / м 4 ∙ с 2 ] = [ Па ] Ответ: E =( 2∙ 1, 05∙ 10 3 ∙ 8∙ 10 2 =1, 68∙ 10 6 Па
• Задача 2. • 2. Как изменится скорость распространения пульсовой волны в сосуде при изменении толщины стенки сосуда от 0, 4 мм до 0, 5 мм. • Решение 12, 125, 1 1 2 h h v v
3. Скорость потока крови в капиллярах равна примерно v 1 = 30 мм/мин, а скорость потока крови в аорте v 2 = 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты. • Решение • Согласно уравнению неразрывности: • S 2 /S 1 =v 1 / v 2 = (45/0, 05)=
4. Найти скорость верхнего слоя жидкости, вязкость которой составляет 1 м. Па с, если при движении потока в ысотой 5 м она д ействует силой 20 м. Н на 200 м 2 дна русла. Решение. Согласно уравнению Ньютона : F=( S v в )/h. v в = ( F h )/( S )=(20 10 -3 5)/ (200 10 -3 )= =0, 5(м/с). Ответ: v в = 0, 5(м/с).
Решение Согласно формуле для числа Рейнольдса: Re=( v d)/ ; откуда: d =( Re )/ ( v ) m=( V)=( v d 2 t)/4 ; т. о. : v =4 m / ( d 2 t ), тогда: d =( Re d 2 t )/4 m. Следовательно: d = 4 m /( Re t )=(4 0, 36)/ (2 10 3 4 10 -3 3, 14 2) 0, 029(м). Ответ: d 0, 029(м)5. Какой диаметр аорты, если прохождении через нее крови массой 0, 36 кг за 2 с течение сохранялось ламинарным? Вязкость крови 4 м. Пас, а критическое число Рейнольдса 2000.
• СПАСИБО • ЗА ЗА ВНИМАНИЕ!
Источник