На дне непрозрачного сосуда высотой

#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
Условие задачи:
Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит заднюю вертикальную стенку. Сколько воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет, находящийся на расстоянии 10 см от задней стенки сосуда на его дне? Ребро сосуда 40 см.
Задача №10.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(l=10) см, (a=40) см, (V-?)
Решение задачи:
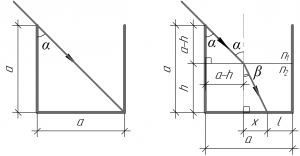 Разумеется, сначала нужно сделать рисунки к задаче. Рассмотрим рисунок слева, он поможет нам найти угол падения луча (alpha). Так как сосуд имеет форму куба, то синус угла (alpha) можно найти следующим образом:
Разумеется, сначала нужно сделать рисунки к задаче. Рассмотрим рисунок слева, он поможет нам найти угол падения луча (alpha). Так как сосуд имеет форму куба, то синус угла (alpha) можно найти следующим образом:
[sin alpha = frac{a}{{sqrt {{a^2} + {a^2}} }}]
[sin alpha = frac{{sqrt 2 }}{2};;;;(1)]
Теперь займемся правым рисунком. Из равенства (1) следует, что угол (alpha) равен 45°, и это очень важный вывод. Значит в прямоугольном треугольнике, образованном лучом, стенкой сосуда и поверхностью воды, оба катета равны (left( {a – h} right)) (смотрите рисунок справа).
Для ситуации на рисунке справа запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin alpha = {n_2}sin beta;;;;(2)]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.
Попытаемся найти синус угла (beta), для чего найдем противолежащий катет (x) в соответствующем прямоугольном треугольнике.
[x = a – l – left( {a – h} right)]
[x = h – l]
Сделаем важную оговорку: так как (x) не может быть меньше нуля, то ({h} > {l}), это пригодится нам в дальнейшем решении.
Тогда синус угла (beta) найдем по формуле (гипотенузу в том же прямоугольном треугольнике найдем по теореме Пифагора):
[sin beta = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }};;;;(3)]
Подставим в уравнение (2) выражения (1) и (3):
[frac{{sqrt 2 {n_1}}}{2} = frac{{{n_2}left( {h – l} right)}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Как Вы должны понимать, физика в этой задаче закончилась, осталась только математика – нужно решить данное уравнение. Перепишем его в следующем виде:
[frac{{sqrt 2 {n_1}}}{{2{n_2}}} = frac{{h – l}}{{sqrt {{{left( {h – l} right)}^2} + {h^2}} }}]
Возведем в квадрат обе части этого уравнения:
[frac{{n_1^2}}{{2n_2^2}} = frac{{{{left( {h – l} right)}^2}}}{{{{left( {h – l} right)}^2} + {h^2}}}]
Перемножим “крест-накрест”:
[n_1^2{left( {h – l} right)^2} + n_1^2{h^2} = 2n_2^2{left( {h – l} right)^2}]
Раскроем скобки в обеих частях уравнения:
[n_1^2{h^2} – 2n_1^2hl + n_1^2{l^2} + n_1^2{h^2} = 2n_2^2{h^2} – 4n_2^2hl + 2n_2^2{l^2}]
Перенесем все в правую часть и сгруппируем:
[left( {2n_2^2 – 2n_1^2} right){h^2} – left( {4n_2^2 – 2n_1^2} right)hl + left( {2n_2^2 – n_1^2} right){l^2} = 0]
Поделим все на (l^2):
[left( {2n_2^2 – 2n_1^2} right){left( {frac{h}{l}} right)^2} – left( {4n_2^2 – 2n_1^2} right)left( {frac{h}{l}} right) + left( {2n_2^2 – n_1^2} right) = 0]
Решим данное квадратное уравнение относительно (frac{h}{l}), для чего перейдем к нахождению дискриминанта:
[D = {left( {4n_2^2 – 2n_1^2} right)^2} – 4left( {2n_2^2 – 2n_1^2} right)left( {2n_2^2 – n_1^2} right)]
Раскрываем скобки:
[D = 16n_2^4 – 16n_1^2n_2^2 + 4n_1^4 – 16n_2^4 + 8n_1^2n_2^2 + 16n_1^2n_2^2 – 8n_1^4]
[D = 8n_1^2n_2^2 – 4n_1^4]
[D = 4n_1^2left( {2n_2^2 – n_1^2} right)]
Учитывая численные значения показателей преломления, нетрудно сделать вывод, что дискриминант – положительный. Тогда корни уравнения следующие:
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm sqrt {4n_1^2left( {2n_2^2 – n_1^2} right)} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
[frac{h}{l} = frac{{4n_2^2 – 2n_1^2 pm 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}]
Посчитаем численное значение корней:
[left[ begin{gathered}
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 2,686 hfill \
frac{h}{l} = frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} – 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}} = 0,614 hfill \
end{gathered} right.]
Как Вы видите, второй корень не удовлетворяют условию ({h} > {l}). Значит уровень воды (h) равен:
[h = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right)l]
Искомый объем воды легко найти по формуле:
[V = {a^2}h]
Окончательно получим:
[V = left( {frac{{4n_2^2 – 2n_1^2 + 2{n_1}sqrt {2n_2^2 – n_1^2} }}{{2left( {2n_2^2 – 2n_1^2} right)}}} right){a^2}l]
[V = left( {frac{{4 cdot {{1,33}^2} – 2 cdot {1^2} + 2 cdot 1 cdot sqrt {2 cdot {{1,33}^2} – {1^2}} }}{{2left( {2 cdot {{1,33}^2} – 2 cdot {1^2}} right)}}} right) cdot {0,4^2} cdot 0,1 = 0,043;м^3 = 43;л]
Ответ: 43 л.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
- Главная
- Вопросы & Ответы
- Вопрос 6960545
Энджелл
более месяца назад
Просмотров : 32
Ответов : 2
Лучший ответ:
Васян Коваль
comment
более месяца назад
Смотри еще 1 ответ ниже
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Еще ответы и пояснения:
Онтонио Веселко
–
более месяца назад
comment
Другие вопросы:
Суррикат Мими
Изобразите векторы скоростей, значения которых равны v1 = 2/3 м/с, v2 = -1 м/с, v3 = 2 м/с, v4 = 1/3 м/с, v5 = 4/3 м/с, v6 = ~4/3 м/с, v7 = -2 м/с Изобразите векторы скоростей, значения которых равны v1 = 2/3 м/с, v2 = -1 м/с, v3 = 2 м/с, v4 = 1/3 м/с, v5 = 4/3 м/с, v6 = ~4/3 м/с, v7 = -2 м/с. Прими…
более месяца назад
Смотреть ответ
Просмотров : 46
Ответов : 1
Васян Коваль
Рассчитайте изменения координат тел за разные промежутки времени при различных значениях скорости. Рассчитайте изменения координат тел за разные промежутки времени при различных значениях скорости.
более месяца назад
Смотреть ответ
Просмотров : 46
Ответов : 1
Онтонио Веселко
Выразите скорости тел в км/ч: а) 10 км/мин = б) 5 км/с = в) 10 м/с = 15 км/мин = 1 км/с = Выразите скорости тел в км/ч:
а) 10 км/мин =
б) 5 км/с =
в) 10 м/с =
15 км/мин = 1 км/с =
15 м/с =
1 км/мин =
0,5 км/с = _
0м/с =
более месяца назад
Смотреть ответ
Просмотров : 24
Ответов : 1
Мари Умняшка
Выразите скорости тел в м/с: а) 10 мм/с = _ б) 30 м/мин = в) 72 км/ч = _ 15 см/с = 180 м/ч = 18 км/ч = Выразите скорости тел в м/с:
а) 10 мм/с = _
б) 30 м/мин =
в) 72 км/ч = _
15 см/с = 180 м/ч = 18 км/ч =
40 км/с =
8640 м/сут = 144 км/ч =
более месяца назад
Смотреть ответ
Просмотров : 18
Ответов : 1
Главный Попко
Придумайте задачу, в которой используется закон прямолинейного равномерного движения. Постройте график такого движения (рис. 13). Придумайте задачу, в которой используется закон прямолинейного равномерного движения. Постройте график такого движения (рис. 13).
более месяца назад
Смотреть ответ
Просмотров : 24
Ответов : 1
Источник
Страница 1 из 2
5. Оптика. Квантовая природа излучения
1. На горизонтальном дне бассейна глубиной h = 1,5 м лежит плоское зеркало. Луч света входит в воду под углом i1 = 45°. Определите расстояние s от места вхождения луча в воду до места выхода его на поверхность воды после отражения от зеркала. Показатель преломления воды n = 1,33.
2. Луч света падает на плоскую границу раздела двух сред, частично отражается и частично преломляется. Определите угол падения, при котором отраженный луч перпендикулярен преломленному лучу.
3. На плоскопараллельную стеклянную (n = 1,5) пластинку толщиной d = 5 см падает под углом i = 30° луч света. Определите боковое смещение луча, прошедшего сквозь эту пластинку.
4. Между двумя стеклянными пластинками с показателями преломления n1 и n2 находится тонкий слой жидкости. Луч света, распространяющийся в первой пластинке под углом i1, (меньше предельного), выходя из слоя жидкости, входит во вторую пластинку под углом i2. Докажите, что в данном случае выполняется закон преломления sin i1 / sin i2 = n2/n1 независимо от присутствия слоя жидкости между пластинами.
5. Человек с лодки рассматривает предмет, лежащий на дне водоема (n = 1,33). Определите его глубину, если при определении “на глаз” по вертикальному направлению глубина водоема кажется равной 1,5 м.
6. Человек с лодки рассматривает предмет, лежащий на дне. Глубина водоема везде одинакова и равна H, показатель преломления воды равен n. Определите зависимость кажущейся глубины h предмета от угла i, образуемого лучом зрения с нормалью к поверхности воды.
7. Предельный угол полного отражения на границе стекло—жидкость iпр = 65°. Определите показатель преломления жидкости, если показатель преломления стекла n = 1,5.
8. Луч света выходит из стекла в вакуум. Предельный угол iпр = 42°. Определите скорость света в стекле.
9. На дне сосуда, наполненного водой (n = 1,33) до высоты h = 25 см, находится точечный источник света. На поверхности воды плавает непрозрачная пластинка так, что центр пластинки находится над источником света. Определите минимальный диаметр пластинки, при котором свет не пройдет сквозь поверхность воды.
10. Длинное тонкое волокно, выполненное из прозрачного материала с показателем преломления n = 1,35, образует световод. Определите максимальный угол α к оси световода, под которым световой луч еще может падать на торец, чтобы пройти световод с минимальным ослаблением.
11. Расстояние a от предмета до вогнутого сферического зеркала равно двум радиусам кривизны. Определите положение изображения предмета и постройте это изображение.
12. На рисунке показаны положения главной оптической оси MN сферического зеркала, светящейся точки S и ее изображения S’. Определите построением положение центра сферического зеркала и его фокуса. Укажите вид использованного зеркала.
14. Вогнутое сферическое зеркало дает действительное изображение, которое в три раза больше предмета. Определите фокусное расстояние зеркала, если расстояние между предметом и изображением равно 20 см.
15. Выпуклое сферическое зеркало имеет радиус кривизны 60 см. На расстоянии 10 см от зеркала поставлен предмет высотой 2 см. Определите: 1) положение изображения; 2) высоту изображения. Постройте чертеж.
25. Выпукло-вогнутая тонкая линза (показатель преломления n) с радиусами кривизны R1 (передняя поверхность) и R2 (задняя поверхность) находится в однородной среде с показателем преломления n1. Выведите формулу этой линзы, рассматривая последовательное преломление света на двух сферических поверхностях.
26. Необходимо изготовить плосковыпуклую линзу с оптической силой Ф = 4 дптр. Определите радиус кривизны выпуклой поверхности линзы, если показатель преломления материала линзы равен 1,6.
28. Определите расстояние a от двояковыпуклой линзы до предмета, при котором расстояние от предмета до действительного изображения будет минимальным.
29. Двояковыпуклая линза с показателем преломления n = 1,5 имеет одинаковые радиусы кривизны поверхностей, равные 10 см. Изображение предмета с помощью этой линзы оказывается в 5 раз больше предмета. Определите расстояние от предмета до изображения.
30. Из тонкой плоскопараллельной стеклянной пластинки изготовлены три линзы. Фокусное расстояние линз 1 и 2, сложенных вместе, равно -f’, фокусное расстояние линз 2 и 3 равно -f”. Определите фокусное расстояние каждой из линз.
31. Двояковыпуклая линза из стекла (n = 1,5) обладает оптической силой Ф = 4 дптр. При ее погружении в жидкость (n1 = 1,7 ) линза действует как рассеивающая. Определите: 1) оптическую силу линзы в жидкости; 2) фокусное расстояние линзы в жидкости; 3) положение изображения точки, находящейся на главной оптической оси на расстоянии трех фокусов от линзы (a = 3f) для собирающей линзы и рассеивающей линзы. Постройте изображение точки для обоих случаев.
Источник
