На дне сосуда в виде усеченного конуса с основаниями
Цель: закрепление изученного
материала и применение его к решению задач.
План урока.
- Дополнительная информация о конусе
(электронное сообщение). 3 мин. - Интеллектуальная разминка. 5 мин.
- Повторение основных сведений о конусе. 5 мин.
- Графический диктант. 7 мин.
- Решение задач по теме. 10 мин.
- Проверочная самостоятельная работа. 10 мин.
- Подведение итогов урока. 3 мин.
- Домашнее задание (подготовка к ЕГЭ.) 2мин.
Ход урока
1. Дополнительная информация о конусе. Материал
заимствован из газеты “Математика”, №42, 2002г.
Электронное сообщение в виде презентации.
А) В геологии существует понятие “конус
выноса”. Это форма рельефа, образованная
скоплением обломочных пород (гальки, гравия,
песка), вынесенными горными реками на предгорную
равнину или в более плоскую широкую долину.
Б) В биологии есть понятие “ конус нарастания”.
Это верхушка побега и корня растений, состоящая
из клеток образовательной ткани.
В) “ Конусами” называется семейство морских
моллюсков подкласса переднежаберных. Раковина
коническая (2-16см), ярко окрашенная. Конусов свыше
500 видов. Живут в тропиках и субтропиках, являются
хищниками, имеют ядовитую железу. Укус конусов
очень болезнен. Известны смертельные случаи.
Раковины используются как украшения, сувениры.
Г) По статистике на Земле ежегодно гибнет от
разряда молний 6 человек на 1000000 жителей (чаще в
южных странах). Этого бы не случилось, если бы
везде были громоотводы, так как образуется конус
безопасности. Чем выше громоотвод, тем больше
объем такого конуса. Некоторые люди пытаются
спрятаться от разрядов под деревом, но дерево не
проводник, на нем заряды накапливаются, и дерево
может быть источником напряжения.
Д) В физике встречается понятие “ телесный
угол”. Это конусообразный угол, вырезанный в
шаре. Единица измерений телесного угла – 1
стерадиан. 1 стерадиан – это телесный угол,
квадрат радиуса которого равен площади части
сферы, которую он вырезает. Если в этот угол
поместить источник света в 1 канделу (1 свечу), то
получим световой поток в 1 люмен. Свет от
киноаппарата, прожектора распространяется в
виде конуса.
2. Интеллектуальная разминка.
а) Ознакомление учащихся с планом урока.
б) Каждой паре учащихся раздаются кроссворды (рисунок
1, рисунок 2). Необходимо угадать принцип
составления кроссвордов и зашифрованные слова.
Слова означают геометрические термины,
относящиеся к стереометрии.
Кроссворд-фантом
Рисунок 1
Кроссворд
Рисунок 2
3. Повторение основных сведений о конусе.
Заполнение опорных листочков. (Заранее
раздается каждому ученику листочек – заготовка.
По желанию, ученики могут сами себе изготовить
опорные листочки).
| Цилиндр | Конус | Усеченный конус |
l – | l – | r – |
4. Графический диктант.
Ответьте на вопросы. Если вы согласны с ответом
или утверждением, то поставьте “__”, иначе “ ”. Первому, правильно
выполнившему все задания, оценка ставиться в
журнал. Все остальные сдают листочки с ответами
на проверку.
- Радиус основания конуса 3 м, высота 4 м. Найдите
образующую. Ответ: 5 м. - Образующая конуса L наклонена к плоскости
основания под углом в 300. Найдите высоту.
Ответ: 2L. - Развертка конуса состоит из треугольника и
круга. - В прямоугольном треугольнике АВС, (рисунок 3), В = 600, ВС = 1. Найдите
длину катета АС, используя теорему Пифагора.
Рисунок 3
Ответ: .
Рисунок 4
Ответ: 8.
- Высота конуса равна 6, радиус основания равен 8.
Найдите боковую поверхность. Ответ: 80. - Радиус оснований усеченного конуса 3м и 6 м,
высота 4 м. Найдите образующую. Ответ 5 м.
Ключ: __ __ __ __.
5. Решение задач по теме “Объем конуса”.
Задача 1. Куча щебня имеет коническую
форму, радиус основания которой 2 м и образующая
3,5 м. Сколько надо возов, чтобы перевезти щебень,
уложенный в кучу?
1 м3 щебня весит 3 т. На один воз грузят 0,5 т.
Решение.
Дано: конус, (рисунок 5)
ОА = 2м,
АР = 3,5м,
1м3 = 3т,
1 воз = 0,5 т.
Рисунок 5
Найти: количество возов.
Решение: V =
Найдем высоту:
h =м м, тогда
V = = 12 м3,
12м3 • 3 т = 36 т в одной куче щебня,
36 : 0,5 = 72 воза потребуется.
Ответ: 72 воза.
Задача 2. Жидкость, налитая в
конический сосуд, имеющий 0,18 м высоты и 0,24 м в
диаметре основания, переливается в
цилиндрический сосуд, диаметр основания
которого 0,10 м. Как высоко будет уровень жидкости
в сосуде?
Решение:
Рисунок 6
r = 0,24 : 2 = 0,12 м, радиус основания конуса,
V конуса = м3,
Составим уравнение:
Ответ: 0,35м.
Задача 3. Равносторонний треугольник
вращается вокруг своей стороны а. Найдите объем
тела вращения.
Решение:
Рисунок 7
Рассмотрим два конуса с радиусами оснований ОС
и высотами ВО и АО.
ВО = АО = 0,5 а,
ОС= ,
V =
Ответ:
6. Проверочная самостоятельная работа.
Вариант 1.
1. Основание треугольника b , высота его h. Найти
объем тела, полученного при вращении его вокруг
основания.
2. Дан прямой круговой конус, (рисунок 8), r = 6 cм, ВСО = 450. Найдите объем
конуса.
Рисунок 8
Вариант 2.
1. Прямоугольный треугольник с катетами 3 и 4
вращается около гипотенузы. Определите объем
полученного тела.
2. Дан прямой круговой конус, (рисунок 9), АВС равносторонний, ВО = 10. Найдите объем
конуса.
Рисунок 9
7. Подведение итогов урока.
Проверка самостоятельной работы.
Вариант 1.
Задача 1.
Решение:
Рисунок 10
V=V1+ V2.
V=
Ответ:
Задача 2.
Решение:
Рисунок 11
Найдем h = BO .
ВОС равнобедренный; ВО =
ОС = 6см.
Итак,
Ответ: 72
Вариант 2.
Задача 1.
Решение: 1 случай (рисунок 12)
Рисунок 12
2 случай (рисунок 13)
Рисунок 13
Ответ: 16 или 12 .
Задача 2.
Решение:
Рисунок 14
Найдем радиус основания конуса. С = 600,
В = 300,
Пусть ОС = а, тогда ВС = 2а. По теореме
Пифагора:
Ответ: .
8. Домашнее задание (подготовка к ЕГЭ).
Задача. Объем конуса равен 1 см3.
Радиус основания уменьшили в 2 раза, а высоту
увеличили в 3 раза. Найдите объем получившегося
конуса. Ответ дайте в см3.
Ответы:
Кроссворд-фантом .
Кроссворд.
Литература:
- Л.С. Атанасян, В.Ф. Бутузов и др. Геометрия.
Учебник для 10 – 11 классов. - Математика. Учебно – методическое приложение к
газете “Первое сентября”, №42, 2002 г. Стр 30. - Н. Рыбкин. Сборник задач по геометрии, ч. II.
Стереометрия, Издательство. “Просвещение”.
Москва, 1965г. - Дидактический материал по геометрии для 11
класса. Разрезные карточки/ Сост. Г.И. Ковалева. –
Волгоград: Учитель, 2004. – 176с. - Гин А.А. Приемы педагогической техники: Свобода
выбора. Открытость. Деятельность. Обратная
связь.: Пособие для учителей, – 2 – е изд. Доп.,
перераб. – Луганск: СПД Резников В.С., 2006, 100с.
Приложение.
Источник
Рассмотрим произвольный
конус и проведем плоскость, параллельную основанию конуса. Эта плоскость пересекает
конус по кругу и разбивает конус на две части. Одна из этих частей будет
конусом, а другую называют усечённым конусом.
Усечённым конусом
называется часть конуса, которая лежит между его основанием и секущей плоскостью,
параллельной основанию.
Основаниями усечённого
конуса называются основание
полного конуса, из которого получен усечённый, и часть секущей плоскости, ограниченная
конической поверхностью (круг).
Образующей усечённого
конусаназывается
часть образующей полного конуса, заключённая между основаниями усечённого
конуса.
Высотой усечённого
конуса называется расстояние
между его основаниями.
Сечение усечённого
конуса плоскостью, которая проходит через его ось, называют осевым сечением усечённого
конуса.
Осевое сечение усечённого
конуса – равнобедренная трапеция, основания которой – диаметры оснований
конуса, боковые стороны – образующие усечённого конуса, высота этой трапеции равна
высоте усечённого конуса.
Боковая и полная поверхность усечённого
конуса.
В качестве величины
боковой поверхности усечённого конуса принимается граница, к которому стремится
величина боковой поверхности правильной вписанной (или описанной) в него
усечённой пирамиды при неограниченном увеличении числа её боковых граней.
Боковая поверхность
усечённого конуса равна произведению суммы длин окружностей оснований на
половину образующей.
Sбок =
πL(R + r),
где R и r – радиусы оснований усечённого конуса, а L – длина
образующей.
Чтобы найти площадь
полной поверхности усечённого конуса необходимо к площади его боковой поверхности
прибавить площади двух его оснований.
Полная поверхность
усечённого конуса равна сумме боковой поверхности и площадей оснований.
Sполн =
πL(R + r) + πR2 + πr2.
Боковая поверхность усечённого
конуса равна произведению высоты тела на длину окружности, радиус которого будет
перпендикуляр, опущенный с середины образующей на высоту тела.
Боковая поверхность усечённого конуса равна
Sбок = 2π × ОА × О1О2.
Развёртка усечённого конуса.
Если поверхность усечённого
конуса разрезать по образующей и окружностям оснований и развернуть так, чтобы
боковая поверхность с основаниями лежали в одной плоскости, то на плоскости получим
фигуру, называемую развёрткой усечённого конуса.
ЗАДАЧА:
Найдите боковую поверхность усечённого конуса, если его образующая
наклонена к плоскости основания под углом
60°,
а площадь осевого сечения равна S.
Пусть дан усечённый конус
СА с площадью осевого
сечения
S и ∠ABO
= 60°.
Найти боковую поверхность Sx усечённого конуса.
В равнобедренной трапеции
ВАDС из вершины А на основание
СВ опустим АМ ⊥
СВ. Обозначим
АВ
= L, ОВ = R, О1А
= r.
В прямоугольном ∆ АМВ из условия
∠ МАВ
= 30°, поэтому
По условию задачи площадь осевого сечения
(R + r)H = S,
или
Умножив обе две части равенства на число π, получим
Учитывая, что боковая поверхность усечённого конуса
Sx = πL(R + r),
находим
ОТВЕТ:
ЗАДАЧА:
Образующая усечённого конуса равна 2а и наклонена к основанию под углом 60°. Радиус одного основания в два раза больше радиуса
второго основания. Найдите каждый из радиусов.
Пусть образующая усечённого конуса АВ = 2а,
а угол наклона образующей к плоскости основания конуса ∠ ВАО1 = 60°.
Учитывая, что
АО1 =
2ВО,
опустим из точки В на плоскость нижнего основания перпендикуляр
ВК ⊥ АО1 тогда
ВО = КО1 = АК.
З ∆ АВК АК = АВ cos∠ ВАК
АК = 2а cos60° = а.
Тогда
АК = КО1 = ВО = а,
АО1 = 2а.
ОТВЕТ: а, 2а.
Задания к уроку 14
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
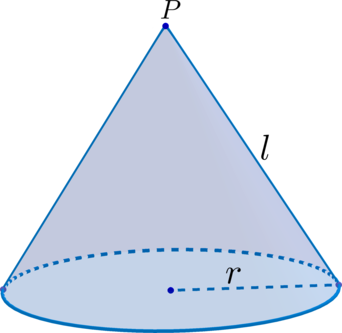
(blacktriangleright) Точка (P) – вершина конуса.
(blacktriangleright) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).
(blacktriangleright) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.
(blacktriangleright) Площадь боковой поверхности конуса ({large{S_{text{бок.пов.}}=pi rl}}), где (r) – радиус основания, (l) – образующая.
(blacktriangleright) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. [{large{S_{text{полн.пов.}}=pi rl+pi r^2=pi r(r+l)}}]
(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}S_{text{осн.}}cdot h=dfrac{1}{3}pi
r^2h}}), где (h) – высота конуса.
Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.
Задание
1
#1886
Уровень задания: Равен ЕГЭ
Площадь боковой поверхности конуса равна (48pi), а площадь основания равна (36pi). Найдите длину образующей конуса.
Если радиус окружности, лежащей в основании конуса обозначить за (r), а длину образующей за (l), то площадь основания и площадь боковой поверхности конуса выразятся по формулам: (S_{text{осн.}} =
pi r^2), (S_{text{бок.пов.}} = pi r l). Из первой формулы следует: (pi r^2 = 36pi) (Rightarrow) (r^2 = 36) (Rightarrow) (r
= 6) (Rightarrow) (6pi l = 48pi) (Rightarrow) (6l = 48) (Rightarrow) (l = 8).
Ответ: 8
Задание
2
#1887
Уровень задания: Равен ЕГЭ
Площадь боковой поверхности конуса равна (48pi), а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна (36pi). Найдите высоту усеченного конуса, если высота исходного конуса равна (10).
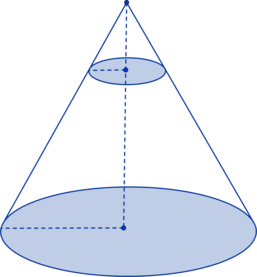
Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: (S_{text{мал}} = 48pi – 36pi = 12pi). Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: [frac{S_{text{бол}}}{S_{text{мал}}} = k^2 =
frac{48pi}{12pi} = 4Rightarrow k = 2]
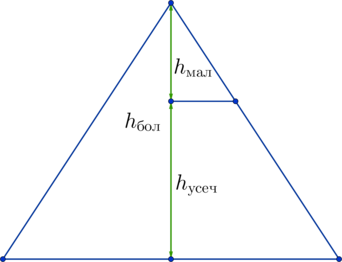
Тогда высоты конусов относятся друг к другу: (dfrac{h_{text{бол}}}{h_{text{мал}}} = dfrac{10}{h_{text{мал}}}
= k = 2). Тогда
[h_{text{мал}} = 5Rightarrow h_{text{усеч}} = h_{text{бол}}
– h_{text{мал}} = 10 – 5 = 5]
Ответ: 5
Задание
3
#962
Уровень задания: Сложнее ЕГЭ
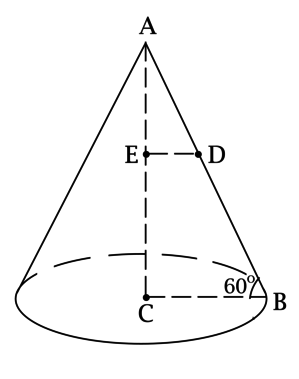
На высоте конуса с вершиной (A), центром основания (C) и радиусом основания (R = 4) отметили точку (E) такую, что расстояние от неё до основания равно (sqrt{3}(4-pi^{-0,5})). Известно, что угол между образующей конуса и плоскостью основания равен (60^circ). Найдите площадь сечения (T) конуса, проходящего через точку (E) и параллельного основанию конуса.

Рассмотрим треугольник (ABC), где (B) – некоторая точка на окружности основания. Так как (AC) – высота конуса, то (ACperp CB), тогда (angle CAB = 90^circ – angle ABC = 30^circ), следовательно, (AB = 2CB = 8). По теореме Пифагора [AC = sqrt{AB^2 – CB^2} = 4sqrt{3}.]
Обозначим через (D) точку пересечения плоскости сечения (T) и (AB). Рассмотрим треугольник (AED): [AE = AC – CE = 4sqrt{3} – sqrt{3}(4 – pi^{-0,5}) = sqrt{dfrac{3}{pi}}.]
Так как сечение (T) параллельно плоскости основания, а (AC) – высота конуса, то (ACperp ED), тогда (triangle AED) – прямоугольный и (angle EAD = 30^circ), откуда [ED = AEcdot mathrm{tg}, angle EAD = sqrt{dfrac{3}{pi}}cdot dfrac{1}{sqrt{3}} = dfrac{1}{sqrt{pi}} = r] – радиус сечения (T).
Таким образом, площадь сечения (T) равна (pi r^2 = picdotdfrac{1}{pi} = 1).
Ответ: 1
Задание
4
#963
Уровень задания: Сложнее ЕГЭ
Радиусы оснований усечённого конуса равны [r = dfrac{2}{sqrt[4]{2}sqrt{pi}}qquad text{и}qquad R = dfrac{10}{sqrt[4]{2}sqrt{pi}},] а угол между его образующей и основанием равен (45^circ). Найдите площадь боковой поверхности этого усечённого конуса.
Обозначим центры оснований усечённого конуса через (A) и (E), так что (A) – центр большего основания. Отметим на большем основании точку (C), а точку меньшего основания, через которую проходит образующая, выходящая из (C), обозначим через (D).
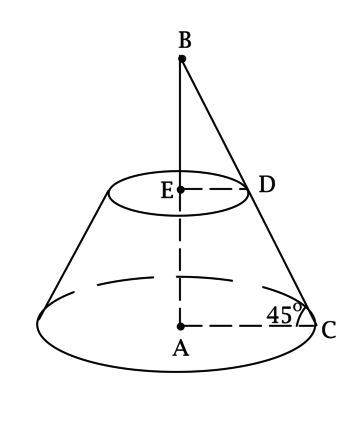
Высота (AE) и образующая (CD) лежат в одной плоскости. Обозначим точку их пересечения через (B).
Так как (AE) – высота, то (AEperp CD) и (AEperp AC).
Рассмотрим прямоугольный треугольник (BAC):
в нём (angle BCA = 45^circ), тогда [AB = R = dfrac{10}{sqrt[4]{2}sqrt{pi}},qquadqquad BC = Rsqrt{2} = dfrac{10sqrt{2}}{sqrt[4]{2}sqrt{pi}}.]
Рассмотрим прямоугольный треугольник (BED):
так как (angle EBD = 45^circ), то [BE = r = dfrac{2}{sqrt[4]{2}sqrt{pi}},qquadqquad BD = rsqrt{2} = dfrac{2sqrt{2}}{sqrt[4]{2}sqrt{pi}},] тогда (EA = AB – BE = R – r), (DC = BC – BD = Rsqrt{2} – rsqrt{2} = sqrt{2}(R – r)). [S_{text{бок}} = pi(R + r)cdot I,] где (I) – образующая, тогда [S_{text{бок}} = pi(R + r)cdotsqrt{2}(R – r) = sqrt{2}pi(R^2 – r^2) = sqrt{2}pileft(dfrac{100}{sqrt{2}pi} – dfrac{4}{sqrt{2}pi}right) = 96.]
Ответ: 96
Старшеклассникам, которые готовятся к сдаче ЕГЭ по математике, непременно стоит научиться вычислять площадь и другие неизвестные параметры конуса. Как показывает практика предыдущих лет, подобные задания из раздела «Геометрия в пространстве» вызывают у выпускников определенные сложности.
При этом понимать, как найти площадь боковой поверхности или, к примеру, сечения конуса, параллельного основанию, должны все учащиеся, независимо от уровня их подготовки. Это позволит им успешно пройти аттестационное испытание по математике.
Базовая информация, которую стоит запомнить
- Конус представляет собой геометрическое тело, которое образовано совокупностью круга, точки, находящейся вне его плоскости, и лучей, соединяющих заданную точку с точками круга. Его высотой называется перпендикуляр, который опущен из вершины на плоскость основания.
- Все образующие конуса равны между собой.
- Осевое сечение конуса представляет собой равнобедренный треугольник. Основание этой фигуры равняется двум радиусам. Боковые стороны треугольника равны образующим конуса.
Занимайтесь вместе с сайтом «Школково»!
Чтобы не допускать распространенных ошибок при решении задач по теме «Конус», выбирайте наш математический портал. Здесь есть весь необходимый материал для изучения разделов, требующих повторения.
Специалисты образовательного проекта «Школково» предлагают новый подход к подготовке к экзамену, предполагающий переход от простого к сложному. Вначале мы даем полную теорию, основные формулы и элементарные практические задачи с решением, в том числе и по теме «Конус», а затем постепенно переходим к заданиям экспертного уровня, которые также встречаются в ЕГЭ. Вся необходимая информация представлена в разделе «Теоретическая справка».
Вы также можете сразу приступить к решению онлайн-задач на вычисление высоты усеченного конуса, площади его боковой поверхности, объема, а также похожих задач на вычисление, например, нахождению объема или площади сечения куба. Большая база упражнений представлена в разделе «Каталог». Перечень заданий систематически обновляется.
Проверьте, насколько легко вы сможете определить площадь конуса в режиме онлайн. Если упражнение потребовало от вас минимальных усилий, рекомендуем вам не тратить время на простые задачи и переходить к более сложным. А если затруднения все же возникли, тогда вам непременно стоит находить время в своем ежедневном расписании на дистанционные занятия вместе со «Школково». С нами вы сможете быстро усвоить алгоритм решения задач на расчет объема конуса и других неизвестных параметров.
Источник
