Нахождение жидкости в сосудах
Скопление жидкости в плевральной полости ежедневно диагностируют в среднем у 1 млн человек в мире. Наиболее частые причины – сердечная недостаточность (СН), пневмония, онкологические процессы, тромбоэмболия легочной артерии, туберкулез.
Классификация и диагностика плевральной жидкости
Объем жидкости в плевральной полости регулируется балансом между гидростатическим и онкотическим давлением в кровеносных сосудах висцеральной и париетальной плевры и лимфатическим дренажом. Норма составляет около 1,0–15 мл. Когда этот баланс нарушается, объем жидкости в плевральной полости увеличивается. Когда объем жидкости достигает 100-300 мл, это можно увидеть на линейной рентгенограмме грудной клетки.
Основная диагностическая процедура для проверки происхождения жидкости – пункция плевральной полости. Она проводится всем пациентам, у которых есть жидкость в плевральной полости, за исключением случаев, когда количество жидкости очень мало, и выполнять пункцию небезопасно.
![]() Пункция плевральной полости
Пункция плевральной полости
После аспирационной пункции плевральной полости в первую очередь оценивают цвет, прозрачность и запах плевральной жидкости. Очень важен характер жидкости: кровотечение (геморрагический плеврит и гематоракс), гнойная или хилозирующая. Плохой запах характерен для эмпиемы плевры, вызванной анаэробными бактериями.
Традиционно жидкость в плевральной полости подразделяется на транссудат и экссудат, диагностические критерии для которых были опубликованы в 1972 году RW Laitas et al. Эти критерии до сих пор используются во многих клиниках по всему миру. Чувствительность критериев составляет 98%, а специфичность – 83%.
- Транссудат. Считается, что транссудат возникает при нарушении баланса онкотического и гидростатического давления. Но, следует иметь в виду возможное попадание в плевральную полость ятрогенной жидкости из-за нежелательной локализации центрального венозного катетера или назогастрального зонда.
- Экссудат. В большей степени вызван воспалительными состояниями, чем необходимыми интервенционными и лечебными процедурами. Воспалительные процессы увеличивают секрецию белка в плевральной полости, так что белок затем перемещается в жидкости. Накапливаясь, он стимулирует дальнейшее развитие процесса.
![]() Экссудат и транссудат
Экссудат и транссудат
Диагностика экссудата и транссудата
Было замечено, что экссудат может быть неправильно диагностирован у пациентов, получающих диуретики, из-за повышенного уровня белка в плевральной жидкости. В таких случаях рекомендуется дополнительно исследовать уровни альбумина в плевральной жидкости и крови.
- Если градиент альбумина (концентрация альбумина в крови минус концентрация альбумина в плевральной жидкости) превышает 12 г / л, плевральная жидкость представляет собой транссудат;
- Если менее 12 г / л – экссудат.
Если обнаруживается, что жидкость является транссудатом, дальнейшее исследование нецелесообразно. В этом случае необходимо уточнить, какая из 4 наиболее частых причин – сердечная недостаточность, цирроз печени, нефротический синдром или тромбоэмболия легочной артерии – преобладает.
Если жидкость представляет собой экссудат, требуется дополнительное исследование – цитологическое, биохимическое, бактериологическое.
Как и в случае с другими заболеваниями, важно оценить вышеуказанные причины плеврального выпота, целенаправленно собрать анамнез:
- рецидивирующие или существующие заболевания (сердце, почки, печень и т. д.);
- условия труда или жизни (воздействие асбеста);
- вредные привычки (курение, алкоголь или употребление наркотиков);
- травмы грудной клетки или медицинские вмешательства;
- использованные или ранее использованные лекарства;
- возможные опухолевые процессы.
Другие более редкие заболевания можно исключить, собрав анамнез и вернувшись к ним, если ни одно из основных заболеваний не подтверждено.
Также важно время появления клинических признаков плеврита (после рецидивирующей пневмонии, травмы, медицинского вмешательства или по другим причинам).
Пациент может жаловаться на кашель, одышку и боли в плевре. Эти симптомы могут быть изолированными или их комбинацией, но они не являются специфическими и редко помогают определить причину скопления жидкости в плевральной полости.
Назначаются следующие исследования
- Спиральная компьютерная томография грудной клетки. КТ помогает дифференцировать заболевания паренхимы плевры и легких, помогает лучше оценить поражение интерстициальных лимфатических узлов, паренхиму легких, плевру, грудную стенку, костные структуры, изменения средостения, локализацию и распространение патологического процесса, отек плевры.
- Ультразвуковое исследование. Самый простой и доступный тест для определения жидкости в плевральной полости, ее количества, даже продолжительности нахождения жидкости в плевральной полости. По специфике он эквивалентен компьютерной томографии. В литературе указано, что количество жидкости можно определить по расстоянию от легкого до париетальной плевры. Конечно, во время измерения расстояние может измениться, но для эталонного количества жидкости этого достаточно.
- Передняя рентгенограмма грудной клетки. На снимках плеврит наблюдается при его объеме более 150-170 мл. Обычно это тень в углах костодиафрагмы.
- Магнитно-резонансная томография. Позволяет увидеть изменения в плевре, отличить твердые структуры от жидкости в плевральной полости, а также оценить изменения в диафрагмальной плевре и стенке грудной клетки. Однако сравнительных исследований контрастной компьютерной томографии и магнитно-резонансной томографии нет, поэтому трудно судить, какое исследование лучше.
- Бронхоскопия. Для дифференциальной диагностики плевральной жидкости (новообразования, туберкулез, инородное тело) важна в следующих случаях:
- инфильтрация легких видна на рентгенограмме грудной клетки или компьютерной томограмме;
- если есть кровотечение;
- когда в плевральной полости много жидкости (более 3/4 плевральной полости).
![]() Передняя рентгенограмма грудной клетки
Передняя рентгенограмма грудной клетки
Лечение при скоплении плевральной жидкости
Жидкость в плевральной полости является следствием других заболеваний, поэтому лечение также зависит от первопричины.
Если имеется большое количество жидкости, вызывающей дискомфорт и нарушение дыхания, ее следует удалить проколом или дренировать.
Уровень жидкости, вызванный приемом лекарств, невысок. Если есть подозрение на фармакологическое происхождение жидкости, обычно эффективно прекращение приема препарата (прокаинамид гидралазин, хинидин, нитрофурантоин, кордарон, прокарбазин, метотрексат и т. д.). Такое состояние не требует дальнейшего вмешательства.
В случае гнойной жидкости с pH меньше 7,2, если она инкапсулирована или обнаружены бактерии, необходимо срочное удаление толстым дренажем. У дренированных пациентов при адекватном антибактериальном лечении состояние обычно улучшается в течение недели.
Если по прошествии недели большое количество жидкости остается или увеличивается, что показывает УЗИ или другие методы, следует рассмотреть возможность дренирования плевральной полости и оценить другие причины появления жидкости. Пневмония может быть связана с опухолевым процессом или туберкулезом. В этом случае рекомендуется компьютерная томография.
Жидкость, выделяемая у онкологических больных, обычно является признаком прогрессирования процесса. Средняя выживаемость таких пациентов составляет около 1 года.
Жидкость обычно диагностируется впервые при развитии медленно прогрессирующей одышки. Поскольку этот процесс протекает медленно, пациенты объясняют эти недомогания основным заболеванием и обращаются за помощью, когда уровень жидкости очень высок.
После удаления жидкости пациент чувствует себя намного лучше. Правда, улучшение временное. Жидкость рецидивирует в течение 2-3 недель. Для удаления жидкости производятся повторные проколы плевральной полости. Было замечено, что жидкость лучше удаляется, если применяется плевральный дренаж. Иногда длительное дренирование приводит к самопроизвольному разрастанию плевральной полости. Это альтернатива плевродетической хирургии.
Туберкулезная жидкость обычно проходит спонтанно при адекватной противотуберкулезной терапии.
Хирургическое лечение при наличии жидкости в плевральной полости
Хирургическое вмешательство применяется для выяснения причин образования жидкости при отсутствии других вариантов или в чисто терапевтических целях.
Визуальная контролируемая торакоскопия. Проводится под местной или общей анестезией. Врач исследует плевральную полость, собирает биопсийный материал и удаляет обнаруженную жидкость. При необходимости проводится очищение плевральной полости. Процедура автоматически классифицируется как малоинвазивная.
![]() Визуальная контролируемая торакоскопия
Визуальная контролируемая торакоскопия
Декортикация. Когда плевральная полость по каким-то причинам деформируется, проводят декортикацию – удаляют утолщенную плевру и расслабляют легкие. Если поврежденную плевру не удалить, нарост сдавливает легкие, развивается одышка, потому что легкие не могут хорошо расширяться при дыхании. Это масштабная операция, требующая торакотомии.
Подбор медикаментозной терапии
Для лечения серьезных заболеваний назначаются лекарства. Если жидкость поступает из сердца, наиболее эффективны диуретики, вазодилататоры и другие препараты, влияющие на сердечно-сосудистую систему. Диуретики не помогут, если жидкость вызвана пневмонией, опухолью или туберкулезом.
При эмпиеме плевры, помимо дренажа плевры, наиболее важны антибиотики. Могут применяться комбинации цефалоспоринов и антианаэробных препаратов. В случае неосложненных парапневмонических жидкостей достаточно одного антибактериального агента, направленного против предполагаемого или указанного возбудителя.
Поделиться ссылкой:
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
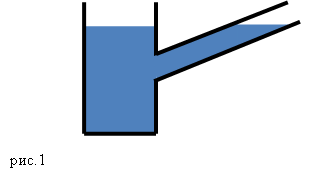
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
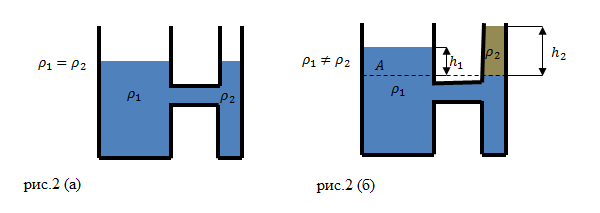
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
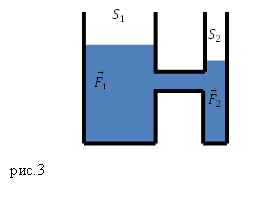
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
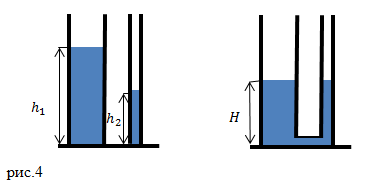
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
1.5. Гидростатика
Давление. Сила давления
Давление равно отношению силы давления к площади. Это универсальное определение относится к твердым телам, жидкости, газу.
Способы увеличения давления: увеличить силу; уменьшить площадь. Давление в твердых телах передается в том же направлении, в котором действует сила. При решении задач (например, тело на наклонной плоскости) рассматриваются проекции сил — давление тела на плоскость и реакция опоры — на оси координат. Направление движения тела, при действии несколкиз сил, не совпадает с направлением силы давления на тело.
Гидростатика. Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково. Это связано с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости:
(ро же аш), где ρ — плотность жидкости, g — ускорение свободного падения.
h – высота столба жидкости или глубина, на котороей измеряется давление.
Сила давления: F = p S . Используя две формулы, находим силу давления на дно сосуда, на боковую грань аквариума и т.п. Экзаменационные задачи на эту тему простые; вычисляйте всё в системе СИ.
Гидростатический парадокс (следствие закона Паскаля): давление на дно сосуда определяется только высотой столба жидкости. И не только на дно, но и вообще на данной глуибне. Независимо от фомы сосуда и его размеров (см. формулу выше).
Поэтому в трех сосудах давление на дно одинаково.
Но сила давления разная — не путаем понятия!
Сообщающиеся сосуды
Сообщающиеся сосуды – сосуды, соединенные между собой (трубкой) или имеющие общее дно.
Уровень жидкости в сообщающихся сосудах располагается горизонтально, если:
поверхности жидкости открыты;
в сосуды налита однородная жидкость;
ни один из сосудов не является капилляром;
в жидкостях нет пузырьков с воздухом.
Давление столбов жидкости на одном горизонтальном уровне одинаково:
Гидравлический пресс – простой механизм, дающий выигрыш в силе. Он представляет собой сообщающиеся сосуды разного сечения. В основе его действия лежит закон Паскаля.
Внешняя сила, действующая на малый поршень, совершает работу. Давление в жидкости одинаково. (Высота столбов жидкостей в цилиндрах пресса меняется, но в задачах это не учитывается.
Такой пресс может работать в любом положении и в невесомости.)
Сила давления жидкости, действующая на большой поршень совершает полезную работу. Из меньшего цилиндра в больший перемещается некоторый объем жидкости — при этом перемещение меньшего поршня больше. Выигрыш в силе аналогичен действию рычага. Затрачиваемая и совершаемая работы одинаковы (если КПД 100%).
Источник
Сообщающиеся сосуды
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ — плотность жидкости; $g$ — ускорение свободного падения; $h$ — высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
где $_1$ и $_2$ — плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
Пусть площадь первого поршня, к которому прикладывают силу $>_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила $>_2$. Давление, которое создает первый поршень равно:
Второй поршень давит на жидкость:
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
величина первой силы больше модуля силы $F_2$ в $frac$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана — уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ — площадь сечения правого сосуда. Объемом трубки пренебречь.
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
где $S_$ — площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
где $S_$ — площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
Ответ. $Delta h=frac>S_2$
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
Ответ. $F_1=F_2frac$
Источник
Закон сообщающихся сосудов и его применение.
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Содержание статьи
Закон сообщающихся сосудов
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Источник
Источник
