Наиболее вероятная скорость молекул в сосуде
Степенями свободы характеризуется способность системы (в нашем случае молекулы) совершать независимые движения. В соответствии с видами механического движения различают поступательные, вращательные и колебательные степени свободы.
Числом степеней свободы механической системы называется количество независимых величин, однозначно определяющих ее положение и конфигурацию в пространстве.
Положение материальной точки в пространстве полностью определяется заданием всех ее координат, т.е. материальная точка обладает тремя степенями свободы. Если рассмотреть абсолютно твердое тело, то оно обладает тремя поступательными степенями свободы и тремя вращательными, т.е. положение абсолютно твердого тела определяется тремя координатами его центра масс и тремя координатами, определяется возможные вращения тела вокруг трех взаимно – перпендикулярных осей. Система из N материальных точек, между которыми нет жестких связей, обладает 3N степенями свободы, т.е. поступательными + вращательными + колебательными (колебания происходят вдоль связей). Любая жесткая связь, которая устанавливает неизменное расположение 2 точек, уменьшает число степеней свободы на единицу. Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5, причем 3 из них поступательные, а 2 – вращательные. Опыт показывает, что вращение вдоль оси, проходящее через центры обоих атомов двухатомной молекулы, может быть возбуждено при очень высокой температуре, поэтому оно обычно не учитывается и это справедливо для большого диапазона температур.
Если атомы в молекулах не жестко связаны друг с другом, то они могут совершать колебания относительно друг друга. Таким образом, если молекула состоит из N атомов не жестко связанных друг с другом, то она имеет 3N степеней свободы, из которых 3 степени свободы поступательные, 3 – вращательные (за исключением случая, когда все атомы расположены на одной прямой, тогда вращательных степеней свободы только две), а остальные 3N-6 для нелинейной молекулы, или 3N-5 для линейной являются колебательными степенями свободы.
Например, для трехатомной молекул (в виде треугольника) с тремя жесткими связями будет 3х3-3=6 степеней свободы (из них 3 поступательные и 3 вращательные). Для той же молекулы с нежесткими связями будет 3х3=9 степеней свободы (из них 3 поступательные, 3 вращательные3 колебательные).
Закон равнораспределения по степеням свободы гласит, что если система молекул находится в состоянии теплового равновесия при температуре T, то средняя кинетическая работа равномерно распределена между всеми поступательными и вращательными степенями свободы и для каждой поступательной или вращательной степени она равна kT/2 , а энергия, приходящаяся на колебательную степень свободы, равна kT.
Если число степеней жесткой молекулы обозначить i , то ее средняя энергия будет ikT/2, а внутренняя энергия одного моля газа будет U= NAikT/2=iRT/2 (так как NAk=R). Следовательно,
(1)
(2)
Если молекула нежесткая, то при расчете число колебательных степеней свобода необходимо удвоить.
Трудности классической теории теплоемкости газов состоят в следующем. Из формул (1) и (2) следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры. В общем случае, молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.
Из качественной экспериментальной зависимости молярной теплоемкости водорода (рис.1) следует, что для него СVзависит от температуры: при низкой температуре (< 50 К) CV =3/2 R,при комнатной Сv = 5/2 R и очень высокой CV= 7/2 R). Это можно объяснить, предположив, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к этим двум видам движения добавляются еще колебания молекул.
Расхождение теории и эксперимента объясняется тем, что при вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна для возбуждения колебаний или вращения, то эти колебания или вращения не вносят своего вклада в теплоемкость (соответствующая степень свободы «замораживается» — к ней неприменим закон равного распределения энергии).
Этим объясняется, что теплоемкость моля двухатомного газа (например, водорода при комнатной температуре равна 5/2R вместо 7/2R. Аналогично можно объяснить уменьшение теплоемкости при низкой температуре («замораживаются» вращательные степени свободы) и увеличение при высокой («возбуждаются» колебательные степени свободы).
Рис.1.
В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям (v), которое подчиняется определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. При его выводе Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля, действующие на газ, отсутствуют. Закон Максвелла представлен в виде некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) представляет собой отношение доли (относительного количества) молекул dN(v)/N, скорости которых лежат в интервале от v до v + dv, в величине этого интервала dv.
(1)
Применяя методы теории вероятности, Максвелл нашел функцию f(v), т.е. закон для распределения молекул идеального газа по скоростям:
(2)
Здесь mo – масса одной молекулы.
Из (2) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и температуры Т.
Рис.1.
Рис.2.
График функции распределения приведен на рис.1. Из графика следует, что функция распределения стремится к нулю при v®0 и v®¥ и проходит через максимум при некоторой скорости vв, называемой наиболее вероятной скоростью, причем этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно vв. Площадь под данной кривой равна единице, т.е.
.
Значение наиболее вероятной скорости можно найти, продифференцировав выражение (2) по аргументу v и приравняв результат нулю, используя условие для максимума выражения f(v):
(3)
Из формулы (3) следует, что при повышении температуры (T2>T1) максимум функции распределения молекул по скоростям (рис.2) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, так как общее число молекул газа не зависит от температуры. Поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.
В молекулярно-кинетической теории пользуются понятием средней арифметической скорости vа поступательного движения молекул идеального газа, вычисляемой из закона распределения:
(4)
и средней квадратичной скорости поступательного движения молекул
(5)
Скорости, характеризующие состояние газа: 1) наиболее вероятная (3), средняя арифметическая (4) и средняя квадратичная (5), представлены на рис.1.
Можно ввести также распределение молекул идеального газа по энергиям определяет долю dN(e)/N из общего числа N молекул, которые имеют кинетические энергии e = mv2/2, заключенные в интервале от e до e + de:
где f(e) — функция распределения молекул по энергиям.
Определим в качестве примера среднюю кинетическую энергию <ε> молекулы идеального газа:
Источник
3.3. Распределение Максвелла
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.
Рис. 3.3
Задачу о распределении молекул по скоростям следует сформулировать следующим образом.
Пусть в единице объема n молекул. Какая доля молекул
имеет скорости от v1 до v1 + Δv? Это
статистическая задача.
Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь
какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика.
Необходимые измерения показали, что доля молекул ,
отнесенная к интервалу скорости Δv, т.е. ,
имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории
вероятности определил эту функцию. С тех пор она называется функцией распределения молекул
по скоростям или законом Максвелла.
Аналитически она выражается формулой
| , |
где m – масса молекулы, k – постоянная Больцмана.
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной
скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя
скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул
в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
или
| . |
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал
скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
| . |
Сопоставляя все три скорости:
1) наиболее вероятную ,
2) среднюю ,
3) среднюю квадратичную , –
видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало (рис. 3.4).
Рис. 3.4
При изменении температуры газа будут изменяться скорости движения всех молекул, а,
следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться
вправо при повышении температуры и влево при понижении температуры. Высота максимума
не будет оставаться постоянной. Дело в том, что площадь заштрихованной фигуры численно
равна доле общего числа молекул n,
которую образуют молекулы со скоростями в указанном интервале. Общая площадь, ограниченная
кривой распределения и осью абсцисс (скоростей), таким образом, равна единице и не меняется
при изменении температуры (рис. 3.5). Поэтому высота максимума и меняется при изменении
температуры.
Рис. 3.5
Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях. Слева от максимума кривые идут круче, чем справа. То, что кривая распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асимптотически приближается к оси абсцисс при бесконечно больших скоростях, следует, что молекул с очень большими скоростями мало. Это легко объяснимо. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при которых она получает энергию, и ни одного столкновения, при котором она ее теряет. А такая ситуация маловероятна.
Источник
Определение 1
С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.
Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.
Чтобы лучше объяснить данный вопрос, начнем с введения такого понятия, как пространство скоростей. Оно изображено схематически на рисунке 1.
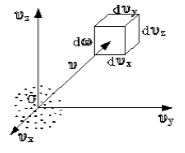
Рисунок 1
Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: “Как именно будут распределяться молекулы в пространстве скоростей”?
Очевидно, что данное распределение не будет равномерным. Если в пространстве мы выделим параллелепипед, имеющий объем dω=dυxdυydυz, то в нем окажется dNυ молекул. Обозначим буквой N число молекул газа, тогда f(v) будет некоторой функцией скорости.
Распределение Максвелла
Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.
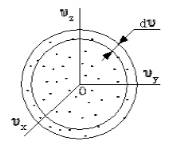
Рисунок 2
Определим, из скольких молекул состоит шаровой слой dυ. Разделим найденное выше число на количество частиц (N) и получим вероятность dWυ того, что пределы модуля скорости молекулы равны υ – υ+dv.
Здесь F(v) является функцией распределения вероятности значения v. Впервые данная функция теоретически была получена Д. Максвеллом.
Определение 2
Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:
dNυ=N4πm02πkT32exp-m0υ22kTυ2dυ.
Здесь υ=υx2+υy2+υz2, масса молекулы равна m0, а k – постоянная Больцмана.
По проекциям скоростей распределение Максвелла может быть записано так:
dN=Nfυxfυyfυzdυxdυydυz.
Важно учесть, что:
fυi=m02πkT12exp-m0υi22kT (i=x,y,z).
Параметры υx, υy, υz означают проекции скоростей молекул на оси координат.
Также возможен следующий вариант записи распределения Максвелла:
dN=N4πυver3exp-υυver2υ2dυ.
Здесь υυer обозначает наиболее вероятную скорость движения молекулы.
Как выглядит распределение Максвелла на графике
Кривая распределения молекул по скоростям на графике выглядит так:
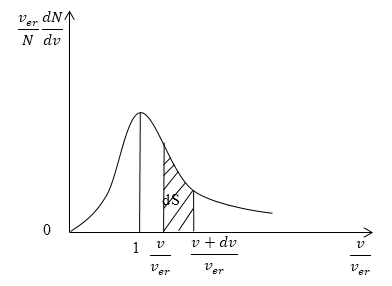
Рисунок 3
При этом доля тех молекул, которые движутся со скоростями в интервале от υ до υ+dυ будет пропорциональна площади dS, которая на графике обозначена штриховкой.
Определение 3
Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:
∫0∞f(υ)dυ=1.
Оно называется условием нормировки функции распределения.
Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.
Пример 1
Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре Т в равновесном состоянии.
Решение
Нам потребуется распределение Максвелла (распределение по модулям скоростей).
dNυ=N4πm02πkT32exp-m0υ22kTυ2dυ.
Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:
dNυdυ=N4πm02πkT322υυerexp-m0υυer22kT-υυer2m02υυer2kTexp-m0υυer22kT=0;
2υυer-υυer2m02υυer2kT=0→1-υυer2m02kT=0→υυer2=2kTm0.
υυer=2kTm0.
Ответ: наиболее вероятно, что скорость газа будет равна υυer=2kTm0.
Пример 2
Условие: изобразите кривые распределения скоростей молекул газа при росте температуры Т.
Решение
Возьмем формулу наиболее вероятной скорости из предыдущей задачи.
υυer=2kTm0
Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:
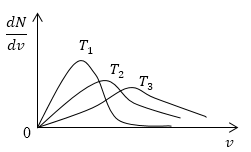
Рисунок 4
Пример 3
Условие: дан график функции, по которой молекулы будут распределяться с учетом проекций скорости υx. Сопоставьте количества молекул, проекции скорости которых будут принадлежать интервалам от нуля до υx1 и от υx1 до υx2.
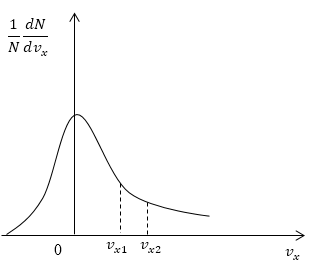
Рисунок 5
Решение
Как мы уже указывали ранее, доля молекул газа, скорости которых лежат в первом интервале, будет пропорциональна площади фигуры, образуемой кривой распределения, вертикальной осью 0 1NdNdυx и вертикальным пунктиром, перпендикулярным оси проекций. Во втором интервале нужная доля будет пропорциональна площади фигуры, ограниченной кривой распределения и вертикальной прямой, параллельной оси ох и проходящей через точку υx1. Очевидно, что площадь первой фигуры будет меньше площади второй. Значит, и молекул, проекции скоростей которых лежат в первом интервале, будет меньше, чем во втором.
Ответ: молекул, имеющих проекции скорости в интервалах: от 0 до υx1 меньше, чем молекул, имеющих проекции скорости в интервалах: от υx1 до υx2.
Источник
Скорости газовых молекул (3.3. Распределение Максвелла)
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.
Рис. 3.3
Задачу о распределении молекул по скоростям следует сформулировать следующим образом. Пусть в единице объема nмолекул. Какая доля молекул имеет скорости от v1 до v1 + Δv? Это статистическая задача.
Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул , отнесенная к интервалу скорости Δv, т.е. , имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.
Аналитически она выражается формулой
| , |
где m – масса молекулы, k – постоянная Больцмана.
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
или
| . |
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
| . |
Сопоставляя все три скорости:
1) наиболее вероятную ,
2) среднюю ,
3) среднюю квадратичную , – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало (рис. 3.4).
Рис. 3.4
При изменении температуры газа будут изменяться скорости движения всех молекул, а, следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться вправо при повышении температуры и влево при понижении температуры. Высота максимума не будет оставаться постоянной. Дело в том, что площадь заштрихованной фигуры численно равна доле общего числа молекул n, которую образуют молекулы со скоростями в указанном интервале. Общая площадь, ограниченная кривой распределения и осью абсцисс (скоростей), таким образом, равна единице и не меняется при изменении температуры (рис. 3.5). Поэтому высота максимума и меняется при изменении температуры.
Рис. 3.5
Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях. Слева от максимума кривые идут круче, чем справа. То, что кривая распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асимптотически приближается к оси абсцисс при бесконечно больших скоростях, следует, что молекул с очень большими скоростями мало. Это легко объяснимо. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при которых она получает энергию, и ни одного столкновения, при котором она ее теряет. А такая ситуация маловероятна.
Закон МАКСВЕЛЛА.
Для газа, находящегося в замкнутом сосуде, результатом многочисленных столкновений молекул между собой и со стенками сосуда, является достаточно быстрое установление универсального распределения молекул по скоростям, которое было теоретически получено Максвеллом в 1860.
На уровне макроскопического описания газамаксвелловскому распределению молекул по скоростям соответствует состояние теплового равновесия в газе: давление и температура во всех местах внутри сосуда оказываются одинаковыми.
В газе, находящемся в состоянии равновесия, установится некоторое стационарное (не меняющееся со временем) распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону.
Такой закон был теоретически выведен Максвеллом в 1859 г. и был опубликован в 1860 г.
МАКСВЕЛЛ, Джеймс Клерк ( 1831 – 1879 )
Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенкой сосуда, беспрерывно меняя свою скорость. Это означает, что в каждый момент времени в газе есть молекулы, которые имеют самые различные скорости. Вместе с тем, поскольку давление и температура в газе остаются постоянными, то, как бы не менялась скорость молекул, среднее значение ее квадрата остается постоянным. Это оказывается возможным лишь при наличии неизменного во времени и одинакового во всех частях сосуда распределения молекул по скоростям.
При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что внешние поля на газ не действуют. Закон Максвелла описывается некоторой функциейf(v), называемой функцией распределения молекул по скоростям.
Сpедняя скоpость опpеделяется фоpмулой
Источник
