Найдите объем первого сосуда
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 — интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 — интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
Решение №1
- Давайте посчитаем объём жидкости в первом сосуде: (V = pi r^2 times 16)
- Посчитаем тот же объём во втором сосуде, предположив, что там вода поднялась на h: (V=pi left(2rright)^2times h=4pi r^2times h)
- Так как переливали один и тот же объём воды, объёмы, вычисленные выше в обоих сосудах, равны. То есть:
(begin{eqnarray} pi r^2times 16 &=& 4pi r^2times h \ 16 &=& 4h \ h &=& 4 end{eqnarray})
Таким образом, высота воды во втором сосуде равна 4 см.
![]()
Решение №2
Объем цилиндрического сосуда выражается через его диаметр и высоту как:
(V=Hfrac{pi d^2}{4})
При увеличении диаметра сосуда в 2 раза высота равного объёма жидкости уменьшится в 4 раза и станет равна 4.
Ответ: 4

ЕГЭ-Центр «Пять с плюсом» основан в 2008 году. С основания и по настоящий момент Центр возглавляет Елизавета Владимировна Глазова, мать пятерых детей, профессиональный педагог и преподаватель русского языка и литературы.
Запрос успешно отправлен. В ближайшее время расширенный доступ будет предоставлен.
– Oбразование как Стиль Жизни
Присылайте свои колонки
и предложения
У вас есть интересная новость
или материал из сферы образования
или популярной науки?
Расскажите нам!
© 2014-2020 Newtonew. 12+
Просветительский медиа-проект об образовании,
посвящённый самым актуальным и полезным
концепциям, теориям и методикам, технологиям
и исследованиям, продуктам и сервисам. Мы
говорим о том, как развиваются и изменяются
образование и наука.
Копирование материалов возможно только
с разрешения редакции Newtonew.
Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.
Авторизация на сайте
Вход через соц.сети:
Напомнить пароль
Введите email, на который вы зарегистрированы:
назад
Пароль выслан
Мы выслали ваш пароль для входа в систему на указанный email.
Не забывайте о том, что вы можете авторизоваться в системе через социальные сети. Если при регистрации в соц.сетях вы указывали тот же email что и на нашем сайте, то после авторизации вы попадете в свой профиль.
Вход через соц.сети:
Подтвердите регистрацию
На указанный e-mail было отправлено письмо со ссылкой. Пожалуйста, перейдите по ссылке для подтверждения.
Вход через соц.сети:
Регистрация подтверждена
Вы успешно зарегистрировались
Источник
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
8
#3045
Уровень задания: Равен ЕГЭ
Объем первого шара равен равен (54). Найдите объем второго шара, если его радиус в (3) раза меньше радиуса первого шара.
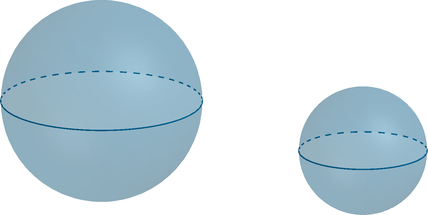
Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{54}{V_2}=dfrac{V_1}{V_2}=
dfrac{frac43 pi ,R_1^3}{frac43 pi
,R_2^3}=left(dfrac{R_1}{R_2}right)^3] Так как радиус второго шара в 3 раза меньше радиуса первого шара, то (R_1=3R_2), следовательно, [dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad
V_2=dfrac{54}{27}=2.]
Ответ: 2
Задание
9
#3053
Уровень задания: Равен ЕГЭ
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.
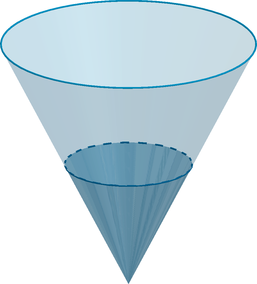
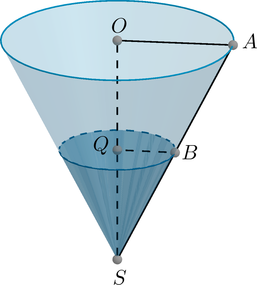
Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:

Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13] Тогда объем налитой жидкости к объему всего сосуда относится как [dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}=
dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot
OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot
dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27}]
Следовательно объем жидкости равен [V_{small{text{ж}}}=dfrac1{27}V=100]
Ответ: 100
Задание
10
#3054
Уровень задания: Равен ЕГЭ
В сосуд цилиндрической формы, объем которого 2400 см(^3), налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.
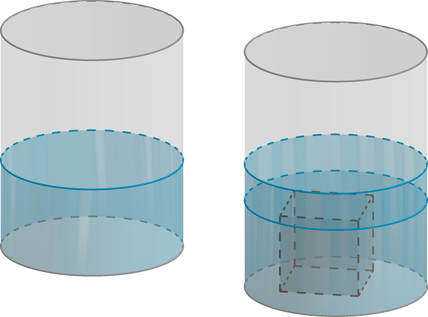
Объем цилиндра вычисляется по формуле (V=pi R^2H), где (R) – радиус основания, (H) – высота. Таким образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем жидкости равен (2400:3=800) см(^3).
Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета. Следовательно, объем предмета равен четверти объема жидкости, то есть (800:4=200) см(^3).
Ответ: 200
Задание
11
#3042
Уровень задания: Равен ЕГЭ
Радиус первого шара равен (6), а радиус второго шара равен (2). Во сколько раз объем первого шара больше объема второго шара?

Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}=
left(dfrac62right)^3=27.] Следовательно, объем первого шара в 27 раз больше объема второго шара.
Ответ: 27
Задание
12
#3050
Уровень задания: Равен ЕГЭ
Объем первого цилиндра равен (16), причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.
Объем цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (V=pi R^2H). Тогда объем первого относится к объему второго цилиндра как [dfrac{16}{V_2}=dfrac{pi,R_1^2,H_1}{pi,R_2^2,H_2}=
left(dfrac{R_1}{R_2}right)^2cdot dfrac{H_1}{H_2}] Из условие следует, что (R_1=frac17R_2), (H_2=frac18H_1), следовательно, [dfrac{16}{V_2}=left(dfrac{frac17R_2}{R_2}right)^2cdot
dfrac{H_1}{frac18H_1}=dfrac1{49}cdot 8 quadRightarrowquad
V_2=98.]
Ответ: 98
Задание
13
#3052
Уровень задания: Равен ЕГЭ
В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Заметим, что из формулы физики (V=frac{m}{rho}) – объем равен отношению массы к плотности.
Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:

Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21] так как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости имеем: [m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho=
dfrac13cdot picdot QScdot QB^2 cdot rho] Следовательно, весь сосуд вмещает этой же жидкости [m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho=
dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot
left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot
75=600 {small{text{грамм}}}] Значит, долить нужно [600-75=525 {small{text{грамм}}}]
Заметим, что в данной задаче использование плотности – чистая формальность.
Ответ: 525
Задание
14
#3055
Уровень задания: Сложнее ЕГЭ
В правильной четырехугольной пирамиде с высотой (h) через точку на боковом ребре, лежащую на расстоянии (frac13h) от плоскости основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите объем полученной меньшей пирамиды, если объем исходной пирамиды равен (54).
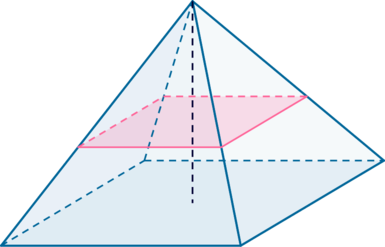
Пусть плоскость провели через точку (A’) на ребре (AS). Так как плоскость параллельна плоскости основания, то она пересечет боковые грани по прямым (A’B’, B’C’, C’D’, D’A’), параллельным соответственно (AB, BC, CD, DA), причем (SA’B’C’D’) – тоже правильная четырехугольная пирамида.
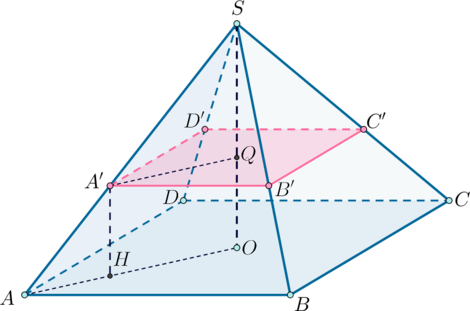
Рассмотрим плоскость (ASO). Проведем (A’Hparallel SO) ((SO) — высота исходной пирамиды). Тогда (A’Hperp ABC). Следовательно, это и есть расстояние, равное (frac13SO), на котором от плоскости основания проведена (розовая) плоскость.
(triangle AA’Hsim triangle ASO), следовательно, [dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad
SA=3AA’ quadRightarrowquad SA’=dfrac23SA] Также отсюда следует, что (SQ=frac23SO).
(triangle ASBsim triangle A’SB’), следовательно, [dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad
A’B’=dfrac23AB] Таким образом, объемы маленькой и большой пирамид относятся как [dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}=
dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot
AB^2}=dfrac{SQ}{SO}cdot
left(dfrac{A’B’}{AB}right)^2=dfrac23cdot
left(dfrac23right)^2=dfrac8{27}] Следовательно, объем маленькой пирамиды равен [V_{{small{text{м}}}}=dfrac8{27}cdot 54=16.]
Ответ: 16
Источник
Наглядная стереометрия
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры — например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии — они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Вариант 13МБ1
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.
- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае. V1 = π r12 h1 V2 = π r22 h2 Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r12 h1 = π r22 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r12 h1)/ π r22
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 . Подставим r2 = 4 r1 в выражение для h1. Получим: h2 =( π r12 h1)/ π (4 r1) 2 Полученную дробь сократим на π, получим h2 =( r12 h1)/ 16 r12 Полученную дробь сократим на r1, получим h2 = h1/ 16. Подставим известные данные: h2 = 80/ 16 = 5 см. Ответ: 5.
Вариант 13МБ2
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы. По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой). Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1 Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй. Ответ: 2.
Вариант 13МБ3
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 1,5 c2 (первая коробка в полтора раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй. Ответ: 6.
Вариант 13МБ4
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Вариант 13МБ5
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
Алгоритм выполнения
- Записываем ф-лу для вычисления объема цилиндра.
- Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
- Формируем формулы для объема 1-го и 2-го цилиндров.
- Вычисляем отношение объемов.
Решение:
Объем цилиндра равен: V=πR2H. Обозначим радиус основания 1-го цилиндра через R1, а его высоту – через Н1. Соответственно, радиус основания 2-го цилиндра обозначим через R2, а высоту – через Н2. Отсюда получим: V1=πR12H1, V2=πR22H2. Запишем искомое отношение объемов:
. Подставляем в полученное отношение числовые данные:
. Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.
Вариант 13МБ6
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Алгоритм выполнения
- Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
- Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
- Переводим результат, полученный в литрах, в куб.см.
Решение:
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1. Отсюда получаем: V2=1,4·5=7 (л). Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см).
Вариант 13МБ7
Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
Алгоритм выполнения
- Записываем ф-лу для расчета объема цилиндра.
- На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
- Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h2.
Решение:
Объем цилиндра равен: V=Sоснh=πR2h. Объем воды в 1-м сосуде: V1=πR12h1. Объем во 2-м сосуде: V2=πR22h2. Приравниваем V1 и V2: πR12h1=πR22h2. Сокращаем на π, выражаем h2:
. По условию R2=2R1. Отсюда:
.
Вариант 13МБ8
От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?
Алгоритм выполнения
- Определяем количество вершин у треугольной призмы.
- Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.
Решение:
Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями правильной треугольной призмы являются правильные треугольники, то вершин у такой призмы 3·2=6 штук.
Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. То есть вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.
Вариант 13МБ9
Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?
Алгоритм выполнения
- Вводим обозначения для линейных параметров коробок и их объемов.
- Определяем зависимость линейных параметров согласно условию.
- Записываем формулу для вычисления объема призмы.
- Адаптируем эту формулу для объемов коробок.
- Находим отношение объемов.
Решение:
Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а1, а для второй а2. Высоты коробок обозначим соответственно h1 и h2. Объемы – V1 и V2.
Согласно условию, h2=4,5h1, а1=3а2. Объем призмы равен: V=Sоснh. Т.к. в основании коробок лежит квадрат, то Sосн=а2. Отсюда: V=a2h. Для 1-й коробки имеем: V1=a12h1. Для 2-й коробки: V2=a22h2. Тогда получаем отношение: Ответ: 2
Вариант 13МБ10
В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
Алгоритм выполнения
- Доказываем, что данные в условии конусы подобны.
- Определяем коэффициент подобия.
- Используя свойство для объемов подобных тел, находим объем жидкости.
Решение:
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
. Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл.
Вариант 13МБ11
Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
Алгоритм выполнения
- Записываем формулу для вычисления объема шара.
- Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
- Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Решение:
Объем шара вычисляется по ф-ле: . Отсюда объем 1-го (большего) шара равен , 2-го (меньшего) шара – . Составим отношение объемов:
Подставляем в полученную формулу числовые данные из условия:
Вывод: объем большего шара в 64 раза больше.
Вариант 13МБ12
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Алгоритм выполнения
- Записываем формулу для определения площади бок.поверхности цилиндра.
- Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
- Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Решение:
Площадь бок.поверхности цилиндра вычисляется так: S=2πRH. Для 1-го цилиндра имеем: S1=2πR1H1. Для 2-го цилиндра: S2=2πR2H2. Составим отношение этих площадей:
Найдем числовое значение полученного отношения:
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Вариант 13МБ13
Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
Алгоритм выполнения
- Записываем формулу для определения массы большего шаров через плотность и объем.
- Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
- Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
- Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
Решение:
Масса большего (1-го) шара равна: m1=ρV1. Объем этого шара составляет V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13. Из этого уравнения выразим плотность: . Масса меньшего (2-го) шара равна: m2=ρV2. Объем шара: V2=(4/3)πR23. В ур-ние для m2 подставим выражения для ρ и V2. Получаем:
Вычисляем m2:
Вариант 13МБ14
В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Алгоритм выполнения
- Определяем часть призмы, соответствующую объему погруженной детали.
- Вычисляем объем детали на основании формулы для определения объема прямой призмы с квадратом в основании.
Решение:
Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь име?
