Найти число молекул газа в сосуде и концентрацию молекул
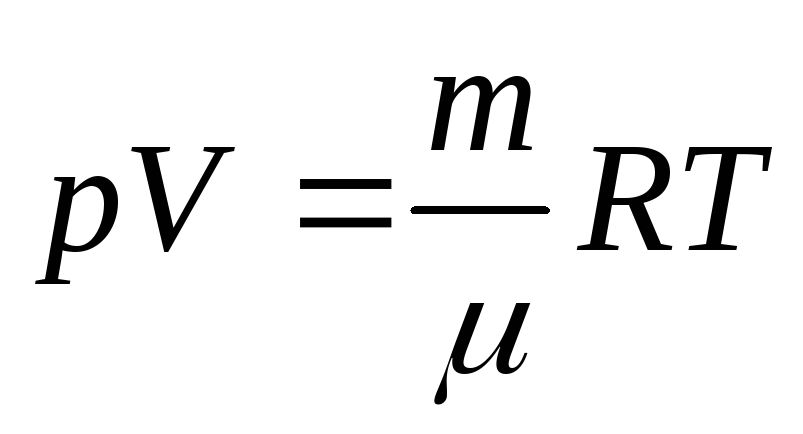
Тема. Решение задач по теме «Скорости газовых молекул. Распределение молекул по скоростям »
Цели
На примерах решения задач познакомить учащихся с основными типами задач и методами их решения.
Ход занятия
Вспомните основные свойства модели идеального газа. Повторите понятие размера молекул и длины свободного пробега. Выведите формулу для длины свободного пробега. Покажите, что длина свободного пробега зависит от давления, под которым находится газ. Подсчитайте число молекул, находящихся в единице объема при нормальных условиях. Обсудите насколько велико это число.
Качественные вопросы
1. Какие гипотезы положены в основу вывода основного уравнения молекулярно-кинетической теории газа?
2. Как правильно сформулировать вопрос о распределении молекул по скоростям?
3. Какой физический смысл имеет функция распределения молекул по скоростям?
4. Чему равна ограниченная кривой распределения молекул по скоростям площадь?
5. Как изменяются с температурой положение максимума кривой функции распределения молекул по скоростям и его высота?
Примеры решения задач
Задача 1.Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Эффективный диаметр молекул принять равным м.
Решение
Средняя длина свободного пробега определяется формулой , где r – радиус молекулы. Так как d = 2r, то , где – число молекул в единице объема, Р – давление и Т – температура. Подставляя значение в формулу для длины свободного пробега, получим
м.
Ответ: м.
Задача 2. Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия ρ = 2,1·10–2 кг/м3, а эффективный диаметр атома гелия d = 1,9·10–2 м.
Решение
Для определения средней длины свободного пробега необходимо знать концентрацию молекул n при данных условиях. Найдем n0. Из уравнения Клапейрона–Менделеева следует, что
.
Следовательно,
.
И для средней длины свободного пробега l получаем расчетную формулу
м.
Ответ: м.
Задача 3. Какое предельное число молекул азота может находиться в сферическом сосуде диаметром D = 1 см, чтобы молекулы не сталкивались друг с другом? Диаметр молекул азота d = 3,1·10–10 м.
Решение
Для того чтобы столкновений молекул друг с другом не было, необходимо чтобы средняя длина свободного пробега λ была не меньше диаметра сосуда D, то есть λ ≥ D. Известно, что
,
где d – эффективный диаметр молекул азота, n – число молекул в единице объема, то есть концентрация молекул. Зная d, можно найти допустимую концентрацию молекул.
.
Максимальное число молекул в сосуде, объем которого , определится следующим образом
.
Ответ: .
Задача 4. Азот находится под давлением Па при температуре Т = 300 К. Найти относительное число молекул азота, скорости которых лежат в интервале скоростей, отличающихся от наиболее вероятной на Δv = 1 м/с.
Решение
Так как интервал скоростей Δv мал, то изменением функции распределения в этом интервале скоростей можно пренебречь, считая ее приближенно постоянной.
.
Подставляем значение наиболее вероятной скорости
;
.
Это и есть решение задачи. Производим вычисления: масса молекулы азота кг, постоянная Больцмана Дж/К. Подставляя численные значения, получим
.
При подсчете необходимо учесть, что определяется относительное число молекул, отличающихся по скорости от наиболее вероятной в обе стороны, то есть интервал равен Δv = 2 м/с.
Ответ: .
Задача 5. Найти температуру газообразного азота, при которой скоростям молекул v1 = 300 м/с и v2 = 600 м/с соответствуют одинаковые значения функции распределения Максвелла молекул по скоростям.
Решение
Запишем функцию распределения для указанных скоростей. По условию задачи значения функции должны быть одинаковы.
;
;
;
;
.
Масса молекулы азота кг.
Постоянная Больцмана Дж/К.
К.
Ответ: = 300 К.
Задача 6. Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.
Решение
Воспользуемся формулой для определения средней квадратичной скорости
,
где – молярная масса газа. Тогда отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах будет равно
,
где- молярная масса неона, – молярная масса гелия. Подставляя численные значения, получим
Ответ: .
Задача 7. Определить: 1) число молекул в 1 мм3 воды, 2) массу молекулы воды, 3) диаметр молекулы воды, считая условно, что молекулы воды шарообразны и соприкасаются.
Решение
Число молекул, содержащихся в массе вещества равно числу Авогадро , умноженному на число молей (- молярная масса вещества)
,
где r – плотность, V – объем вещества. После подстановки числовых значений получим
.
Массу m1 одной молекулы можно определить, разделив массу одного моля на число Авогадро:
кг.
Считая, что молекулы соприкасаются, объем, занимаемый одной молекулой , где d – диаметр молекулы. Отсюда . Так как , где – объем одного моля, то
м.
Ответ: ; кг; м.
Задача 8. Зная, что диаметр молекулы кислорода d = 3·10–10 м подсчитать, какой длины S получилась бы цепочка из молекул кислорода, находящихся в объеме V = 2 см2 при давлении Р = 1,01·105 Н/м2 и температуре Т = 300 К, если эти молекулы расположить вплотную в один ряд. Сравнить длину этой цепочки со средним расстоянием от Земли до Луны м.
Решение
Число молекул кислорода, содержащихся в единице объема, согласно основному уравнению молекулярно-кинетической теории, равно
,
Число молекул в объеме V будет равно . Следовательно, м.
Тогда .
Ответ: м; раз.
Задача 9. Средняя квадратичная скорость молекул некоторого газа vc.к. = 450 м/с. Давление газа р = 7 · 104 Н/м2. Найти плотность газа ρ при этих условиях.
Решение
Из уравнения Клайперона–Менделеева следует: . Учитывая, что , получаем .
Ответ: .
Задания для самостоятельной работы
1. В опыте Штерна источник атомов серебра создает пучок, который падает на внутреннюю поверхность неподвижного цилиндра радиуса R = 30 см и образует на ней пятно. Цилиндр начинает вращаться с угловой скоростью ω = 100 рад/с. Определить скорость атомов серебра, если пятно отклонилось на угол φ = 0,314 рад от первоначального положения.
Ответ: м/с.
2. Сколько молекул газа содержится в баллоне емкостью V = 60 л при температуре Т = 300 К и давлении P= 5·103 Н/м2?
Ответ: .
3. Определить температуру газа, для которой средняя квадратичная скорость молекул водорода больше их наиболее вероятной скорости на Δv = 400 м/с. Масса молекулы водорода т = 3,35·10–27 кг.
Ответ: = 380 К.
4. Вычислить среднее расстояние между центрами молекул идеального газа при нормальных условиях.
Ответ: м.
5. В помещении площадью S = 100 м2 и высотой h = 4 м разлито V1 = 1 л ацетона (СН3)2СО. Сколько молекул ацетона содержится в 1 м3 воздуха, если весь ацетон испарился? Плотность r ацетона 792 кг/м3.
Ответ:
6. Найти число столкновений z, которые произойдут за 1 с в 1 см3 кислорода при нормальных условиях. Эффективный радиус молекулы кислорода принять равным
1,5·10–10 м.
Ответ: .
7. Найти среднюю длину свободного пробега молекул азота при давлении P = 133 Па и температуре t = 27°C.
Ответ: м.
8. Доказать, что средняя арифметическая и средняя квадратичная скорости молекул газа пропорциональны , где P – давление газа; ρ – плотность газа.
Ответ: .
9. Два одинаковых сосуда, содержащие одинаковое число молекул кислорода, соединены краном. В первом сосуде средняя квадратичная скорость молекул равна , во втором – . Какой будет эта скорость, если открыть кран, соединяющий сосуды (теплообмен с окружающей средой отсутствует)?
Ответ: .
Рекомендуемая литература
1. Бутиков Е.И., Кондратьев А.С. Физика. Т.3. Строение и свойства вещества – Москва – Санкт-Петербург. Физматлит. Невский диалект. Лаборатория Базовых Знаний, 2001. С. 170-194.
2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А., Цвецинская Т.С. Задачник по физике – Москва. Физматлит, 2005.
3. Готовцев В.В. Лучшие задачи по механике и термодинамике. Москва-Ростов-на-Дону, Издательский центр «Март», 2004. С. 215-219.
Источник
Задача 1.
Найти число молекул в 1 см3
водорода, если давление газа равно
2,67.104
Па, а средняя квадратичная скорость его
молекул при данных условиях равна 2400
![]() .
.
Дано:
Решение
р
В условиях задачи
концентрацию молекул можно найти двумя
способами:
1. Используем
основное уравнение кинетической теории
где
![]() .
.
= 2,67.104
Па
<Vкв
> = 2400
![]()
V = 1 см3
= 10–6
м3
= 2.10-3![]()
N
– ?
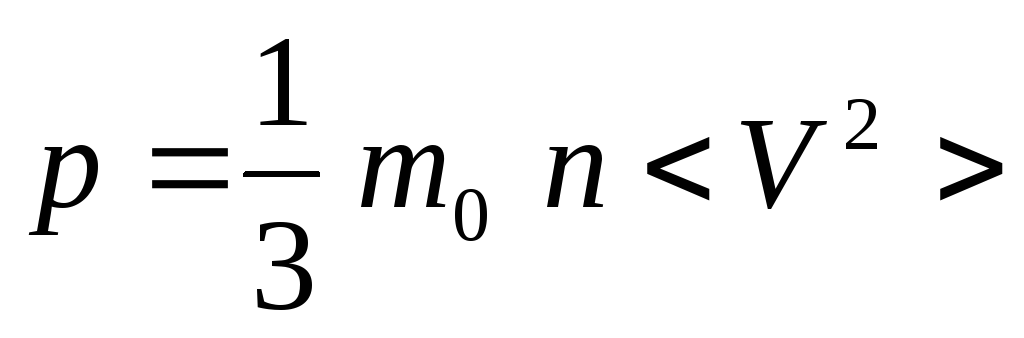 ,
,
где
![]() .
.
Отсюда
![]() .
.
(1)
Массу молекулы
![]() найдем, зная молярную массу и число
найдем, зная молярную массу и число
Авогадро:
![]() .
.
Подставляем в
формулу (1):
![]() .
.
Вычисляем
концентрацию молекул:
![]() = 4,2 .
= 4,2 .
1024
м –3.
Тогда число молекул
N
= n.
V
= 4,2 . 1018
(молекул).
2. Используя связь
давления с концентрацией и формулу
средней квадратичной скорости
![]()
Получаем ту же
формулу для вычисления п.
Ответ: N
= 4,2 . 1018
молекул содержится в 1 см3.
Задача 2.
Плотность некоторого газа 6.10-2![]() ,
,
а средняя квадратичная скорость его
молекул <Vкв
> = 500
![]() .
.
Найти давление, которое газ оказывает
на стенки сосуда.
Дано:Решение
Запишем основное
уравнение молекулярно-кинетической
теории:
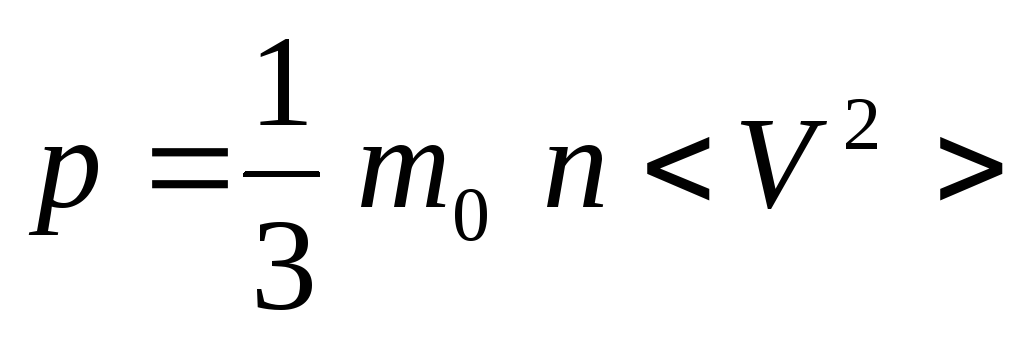 .
.
= 6,0 . 10-2![]()
<Vкв
> = 500
![]()
p
– ?
Преобразуем
это уравнение:
![]()
где N
– число молекул газа, т
– масса газа,
![]() – масса одной молекулы газа.
– масса одной молекулы газа.
Тогда – плотность газа равна произведению массы одной молекулы на концентрацию молекул. Получим
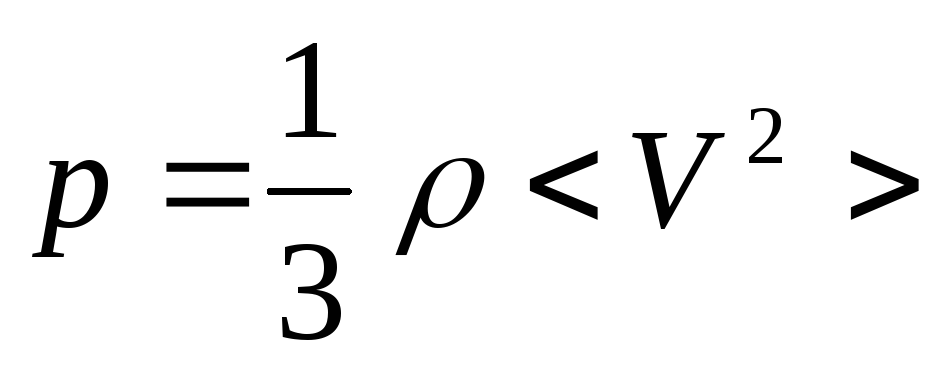
![]() = 5 .
= 5 .
103
Па.
Ответ: p
= 5 . 103
Па.
Задача 3.
В колбе емкостью V
= 100 см3
содержится некоторый газ при температуре
t
= 27 0С.
На сколько понизится давление газа в
колбе, если вследствие утечки из колбы
выйдет N
= 1020
молекул?
Дано:Решение
V
Начальное давление
в колбе
![]() =
=
![]() kT.
kT.
Конечное давление
= 100 см3
= 10-4 м3
t
= 27 0С,
Т
= 300 К
N
= 1020
молекул
р
– ?
![]() =
=
![]() kT,
kT,
где
![]() и
и![]() – концентрации молекул газа в колбе.
– концентрации молекул газа в колбе.
Отсюда получаем изменение давления при утечке газа
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() = 4,14 .
= 4,14 .
103
Па.
Ответ: р
= 4,14 Па.
Задача 4.
Определить среднюю кинетическую энергию
теплового движения всех молекул
двухатомного газа, заключенного в сосуд
объемом 2 л при давлении 1,5 .
105
Па?
Решение
Энергия теплового
движения одной молекулы идеального
газа
![]()
Дано:
V
= 2 л = 2 .10-3
м3
р =
1,5 . 105
Па
i
= 5
<Wк>
– ?
где i
– число степеней свободы молекулы.
В сосуде объемом
V
находится N
молекул. Полная энергия теплового
движения всех молекул равна
![]() .
.
Число молекул газа
N
можно найти с помощью числа Авогадро.
Число молекул в одном моле вещества
одинаково для всех веществ и равно
![]()
![]() .
.
Количество вещества
в молях определяется так:
![]()
где m
– масса вещества;
– его молярная масса.
Тогда число молекул будет равно
![]() .
.
Полная энергия
теплового движения всех молекул вещества
![]()
![]()
![]() .
.
Это выражение
определяет энергию теплового движения
всех молекул данного количества вещества.
Для идеального газа энергия теплового
движения молекул является его внутренней
энергией. Это следует из определения
идеального газа. Внутренняя энергия
обозначается буквой U:
![]() .
.
Для условий нашей
задачи
![]()
![]() (уравнение
(уравнение
Менделеева – Клапейрона).
Следовательно,
![]()
![]() Дж.
Дж.
Из равенства
![]() видно, что внутренняя энергия идеального
видно, что внутренняя энергия идеального
газа зависит только от температуры
газа. Изменение внутренней энергии не
зависит от процесса. Внутренняя энергия
является функцией состояния.
Ответ: <Wк>
= 750 Дж.
Соседние файлы в папке Часть 3
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
