Найти давление смеси газа в сосуде объемом

Уравнение (4.76) позволяет получить расчетные выражения для молярной массы и газовой постоянной смеси газов на основании равенства единице суммы массовых и объемных долей всех газов данной смеси:

При известной молярной массе смеси газовую постоянную смеси проще определить из соотношения

Для определения парциального давления данного газа в смеси можно воспользоваться выражением (4.71). В соответствии с ним

Источник

Физика

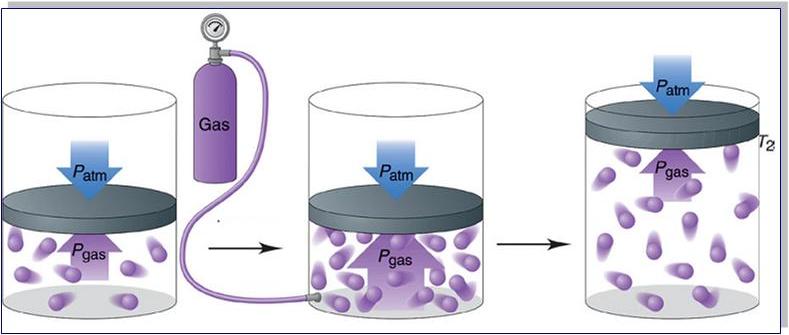
Если идеальные газы находятся в сообщающихся баллонах, разделенных краном, то при открытии крана газы в баллонах смешиваются между собой и каждый из них заполняет объем обоих баллонов.

Для идеального газа (или двух разных газов), находящегося в сообщающихся баллонах , при открытии крана некоторые параметры становятся одинаковыми:

давление газа (или смеси газов) после открытия крана уравнивается:

газ (или смесь газов) после открытия крана занимает весь предоставленный ему объем, т.е. объем обоих сосудов:

где V 1 — объем первого баллона; V 2 — объем второго баллона;

температура газа (или смеси газов) после открытия крана уравнивается:

плотность газа ρ и его концентрация n в обоих баллонах становятся одинаковыми:

Если баллоны имеют одинаковый объем , то массы газа (или смеси газов) в каждом баллоне после открытия крана становятся одинаковыми :

m ′ 1 = m ′ 2 = m ′ = m 1 + m 2 2 ,

где m ′ 1 — масса газа (или смеси газов) в первом баллоне после открытия крана; m ′ 2 — масса газа (или смеси газов) во втором баллоне после открытия крана; m ′ — масса газа (или смеси газов) в каждом баллоне после открытия крана; m 1 — масса газа в первом баллоне до открытия крана; m 2 — масса газа во втором баллоне до открытия крана.

Масса газа, перешедшего из одного сосуда в другой в результате открытия крана, определяется следующими выражениями:

изменение массы газа в первом баллоне

Δ m 1 = | m ′ 1 − m 1 | = | m 1 + m 2 2 − m 1 | = | m 2 − m 1 | 2 ;

изменение массы газа во втором баллоне

Δ m 2 = | m ′ 2 − m 2 | = | m 1 + m 2 2 − m 2 | = | m 1 − m 2 | 2 .

Изменения массы газа (или смеси газов) в обоих баллонах одинаковы :

Δ m 1 = Δ m 2 = Δ m = | m 2 − m 1 | 2 ,

т.е. сколько газа ушло из баллона с большей массой газа — столько же газа пришло в баллон с меньшей массой.

Если баллоны имеют одинаковый объем , то количества газа (или смеси газов) в каждом баллоне после открытия крана становятся одинаковыми :

ν ′ 1 = ν ′ 2 = ν ′ = ν 1 + ν 2 2 ,

где ν ′ 1 — количество газа (или смеси газов) в первом баллоне после открытия крана; ν ′ 2 — количество газа (или смеси газов) во втором баллоне после открытия крана; ν′ — количество газа (или смеси газов) в каждом баллоне после открытия крана; ν 1 — количество газа в первом баллоне до открытия крана; ν 2 — количество газа во втором баллоне до открытия крана.

Количество газа, перешедшего из одного сосуда в другой в результате открытия крана, определяется следующими выражениями:

изменение количества газа в первом баллоне

Δ ν 1 = | ν ′ 1 − ν 1 | = | ν 1 + ν 2 2 − ν 1 | = | ν 2 − ν 1 | 2 ;

изменение количества газа во втором баллоне

Δ ν 2 = | ν ′ 2 − ν 2 | = | ν 1 + ν 2 2 − ν 2 | = | ν 1 − ν 2 | 2 .

Изменения количества газа (или смеси газов) в обоих баллонах одинаковы :

Δ ν 1 = Δ ν 2 = Δ ν = | ν 2 − ν 1 | 2 ,

т.е. сколько газа ушло из баллона с большим количеством газа — столько же газа пришло в баллон с меньшим количеством.

Для идеального газа (или двух разных газов), находящегося в сообщающихся баллонах, при открытии крана давление становится одинаковым:

и определяется по закону Дальтона (для смеси газов) —

где p 1 , p 2 — парциальные давления компонентов смеси.

Парциальные давления компонентов смеси могут быть рассчитаны следующим образом:

с помощью уравнения Менделеева — Клапейрона; тогда давление определяется формулой

p = ( ν 1 + ν 2 ) R T V 1 + V 2 ,

где ν 1 — количество вещества первого компонента смеси; ν 2 — количество вещества второго компонента смеси; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура смеси; V 1 — объем первого баллона; V 2 — объем второго баллона;

с помощью основного уравнения молекулярно-кинетической теории; тогда давление определяется формулой

p = ( N 1 + N 2 ) k T V 1 + V 2 ,

где N 1 — количество молекул первого компонента смеси; N 2 — количество молекул второго компонента смеси; k — постоянная Больцмана, k = 1,38 ⋅ 10 −23 Дж/К.

Пример 26. Определить среднюю молярную массу смеси газов, состоящей из 3,0 кг водорода, 1,0 кг гелия и 8,0 кг кислорода. Молярные массы водорода, гелия и кислорода равны 2,0, 4,0 и 32 г/моль соответственно.

Решение . Средняя молярная масса смеси определяется формулой

где m — масса смеси; ν — количество вещества в смеси.

Массу смеси найдем как сумму масс —

где m 1 — масса водорода; m 2 — масса гелия; m 3 — масса кислорода.

Аналогично найдем количество вещества —

где ν 1 — количество водорода в смеси, ν 1 = m 1 / M 1 ; M 1 — молярная масса водорода; ν 2 — количество гелия в смеси, ν 2 = m 2 / M 2 ; M 2 — молярная масса гелия; ν 3 — количество кислорода в смеси, ν 3 = m 3 / M 3 ; M 3 — молярная масса кислорода.

Подстановка выражений для массы и количества вещества в исходную формулу дает

〈 M 〉 = m 1 + m 2 + m 3 ν 1 + ν 2 + ν 3 = m 1 + m 2 + m 3 m 1 M 1 + m 2 M 2 + m 3 M 3 .

〈 M 〉 = 3,0 + 1,0 + 8,0 3,0 2,0 ⋅ 10 − 3 + 1,0 4,0 ⋅ 10 − 3 + 8,0 32 ⋅ 10 − 3 =

= 6,0 ⋅ 10 − 3 кг/моль = 6,0 г/моль .

Пример 27. Плотность смеси газов, состоящей из гелия и водорода, при давлении 3,50 МПа и температуре 300 К, равна 4,50 кг/м 3 . Определить массу гелия в 4,00 м 3 смеси. Молярные массы водорода и гелия равны 0,002 и 0,004 кг/моль соответственно.

Решение . Чтобы найти массу гелия m 2 в указанном объеме, необходимо определить плотность гелия в смеси:

где ρ 2 — плотность гелия; V — объем смеси газов.

Плотность смеси определяется как сумма плотностей водорода и гелия:

где ρ 1 — плотность водорода.

Однако записанная формула содержит две неизвестные величины — плотности водорода и гелия. Для определения указанных величин требуется еще одно уравнение, в которое входят плотности водорода и гелия.

Запишем закон Дальтона для давления смеси газов:

где p 1 — давление водорода; p 2 — давление гелия.

Для определения давлений газов запишем уравнение состояния в следующей форме:

где R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура смеси; M 1 — молярная масса водорода; M 2 — молярная масса гелия.

Подстановка выражений для давлений водорода и гелия в закон Дальтона дает

p = ρ 1 R T M 1 + ρ 2 R T M 2 .

Получено еще одно уравнение с двумя неизвестными величинами — плотностью водорода и плотностью гелия.

Формулы для расчета плотности и давления смеси образуют систему уравнений:

ρ = ρ 1 + ρ 2 , p = ρ 1 R T M 1 + ρ 2 R T M 2 , >

которую требуется решить относительно плотности гелия.

Для этого выразим плотности водорода из первого и второго уравнений

ρ 1 = ρ − ρ 2 , ρ 1 = M 1 R T ( p − ρ 2 R T M 2 ) >

и приравняем их правые части:

ρ − ρ 2 = M 1 R T ( p − ρ 2 R T M 2 ) .

ρ 2 = M 2 M 2 − M 1 ( ρ − p M 1 R T ) .

Подставим полученное выражение в формулу для вычисления массы гелия

m 2 = M 2 V M 2 − M 1 ( ρ − p M 1 R T )

и произведем расчет:

m 2 = 0,004 ⋅ 4,00 0,004 − 0,002 ( 4,50 − 3,50 ⋅ 10 6 0,002 8,31 ⋅ 300 ) ≈ 13,6 кг.

Масса гелия в указанном объеме смеси составляет 13,6 кг.

Источник

Секретная шпаргалка по химии. 4.2. Состав смеси газов

Команда «Газы!» была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью » Тайны задач по химии? Тяжело в учении — легко в бою!». В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я — зритель в первом ряду.

Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно — хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую «мозгобойню», чтобы вам жизнь медом не казалась. Попробуйте решить.

И.Ю. Белавин, 2005, задача 229

«Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)»

Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду «Газы!» отменять рано. Итак, поехали!

Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.

• Газовая смесь — смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.

• Объемная доля — отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.

• Мольная доля — отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.

• Плотность газа (абсолютная) — определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа — масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.

• Относительная плотность газа (плотность одного газа по другому) — это отношение молярной массы данного газа к молярной массе того газа, по которому она находится

• Средняя молярная масса газа — рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей

Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль , в заданиях ЕГЭ часто встречается.

ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!

Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.

Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.

5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.

Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана

Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху

Плотность паров альдегида по метану равна 2,75. Определите альдегид

Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции — десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!

И.Ю. Белавин, 2005, задача 202

«Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)»

Задачи И.Ю. Белавина — это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: «И снова здравствуйте!», поскольку ЕГЭ с каждым годом становится «все чудесатее и чудесатее». Но это уже совсем другая история. Читайте мои статьи — и вы подстелите соломку под свою ЕГЭшную попу.

Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии https://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы «Решение задач по химии». Я с удовольствием вам помогу.

Репетитор по химии и биологии кбн В.Богунова

Источник

➤ Adblock
detector

Источник

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.

Идеальные газы

Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.

В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.

В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.

Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.

Причина возникновения давления в газах

Давление в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.

Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:

P = F/S

Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:

F*Δt = Δp

Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.

Формула давления газа идеального из молекулярно-кинетической теории

Зависимость давления от объема

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.

Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.

Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:

P = N*m*v2/(3*V)

Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.

Формула давления из уравнения состояния

Эмиль Клапейрон

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:

P*V = n*R*T

Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.

Из уравнения выше легко получить формулу давления газа:

P = n*R*T/V

Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.

Формула давления идеального газа

Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.

Давление в газовой смеси

Давление газовой смеси

Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Пример задачи

Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.

Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:

P = N*m*v2/(3*V)

Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:

m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)

Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.

Источник