Найти давление смеси газов в сосуде
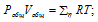
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
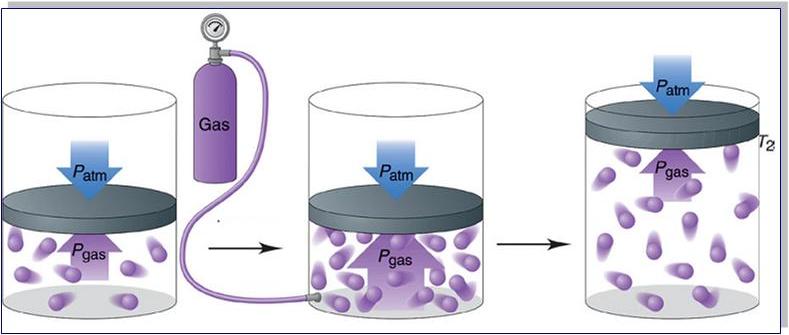
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
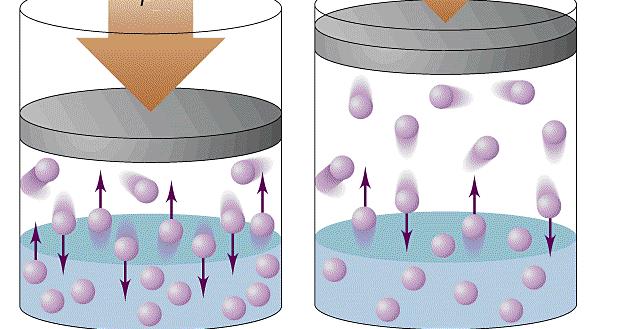
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
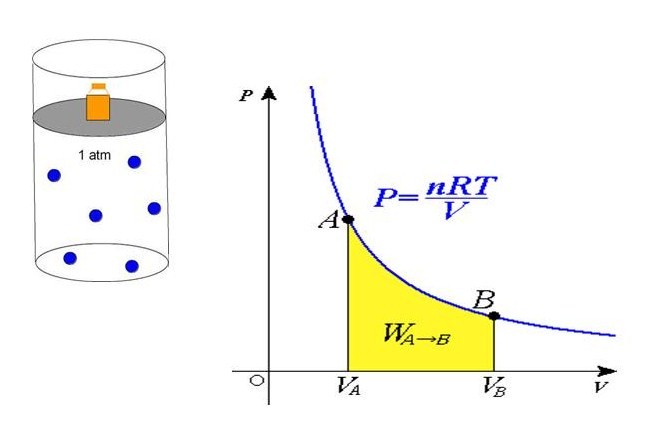
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
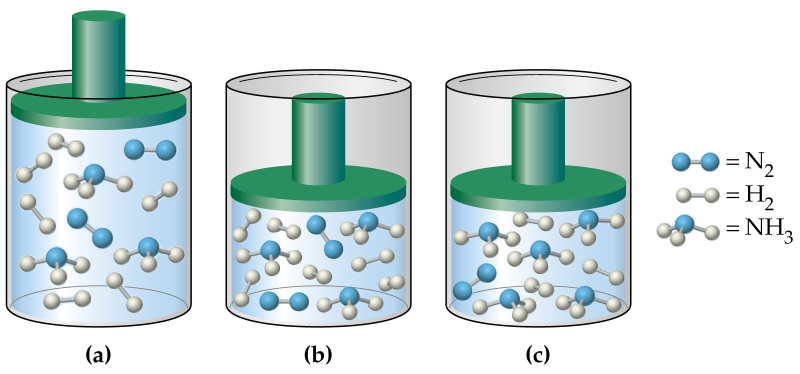
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Задача 41.
Смешивают 0,04м3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м3 кислорода. Общий объем смеси 0,06м3, а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.
Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:
Ответ: Робщ. = 100,8кПа.
Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:
где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа; (A) – мольная доля данного газа.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ: 34,02%NO; 65,98%CO.
Задача 44.
В закрытом сосуде вместимостью 0,6м3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:
, где
– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:
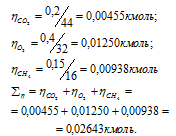
а) Общее давление смеси газов определяем по уравнению:
Тогда:
б) Парциальные давления газов рассчитываем по уравнению:
где Rk и k , соответственно, парциальное давление, и количество газа в смеси.
Тогда
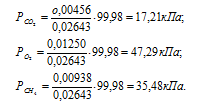
в) Парциальные объёмы газов рассчитаем по уравнению:
Тогда
Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:
Тогда
Ответ:
Задача 45.
Газовая смесь приготовлена из 0,03м3 СН4, 0,04м3 Н2 и 0,01м3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м3. Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Отсюда:
Ответ:
Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:
Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:
где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р0 = 101,325кПа; Т0 = 273К; Р = 104,1кПа; – объём газа при н.у.
Ответ: V0 =6,825л.
Источник
Давление газа — формула. Формула давления газа в сосуде
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Парциальное давление газов — определение, формулы и законы
Трактовка закона
Учёный Дальтон в 1801 году сформировал закон парциальных давлений: Па смеси из идеальных газов равняется сумме рi её компонентов. Уравнение имеет следующий вид: Рсм=n (сумма pi), где n — число долей смеси.
Для определения парциального давления в химии используется отдельный компонент из атмосферного воздуха. При расчете учитывается значение каждого отдельного вещества, их число, температуры с объёмами. При необходимости можно найти общий показатель, сложив давление каждого компонента в отдельности.
Каждый газ в сосуде должен обозначаться как «идеальный». При нормальных условиях они взаимодействуют с углекислым газом, водородом, водой, азотом, водяным паром, кислородом, компонентами крови и прочими компонентами из таблицы Менделеева. При этом не образуются соединения. Отдельные молекулы способны сталкиваться между собой, отталкиваясь, но не деформируясь.
Физические и химические задачи решаются с помощью формулы парциального давления (закон открыли учёные Бойль и Мариотт): (k = P x V). Кроме полного варианта, уравнение записывается сокращённо k = PV, где:
- k равно постоянной величине;
- Р — давление;
- V — объем.
Второстепенные значения
Давление может измеряться в разных величинах: процент, паскаль (Па). Смысл последнего: сила в 1 ньютон приложена к площади в 1 кв. м. Если результат такой зависимости записывается в атмосферах, тогда для его нахождения потребуется учесть, что одна атмосфера равняется 101,325 Па.
Температура идеального газа повышается, если увеличивается объём, а снижается, если уменьшается последний показатель. Такое соотношение может называться законом Чарльза, который имеет следующий математический вид: k = V / T. Значение температуры в уравнении измеряется в градусах Кельвина. Оно зависит от градусов Цельсия. Чтобы его найти, прибавляется 273.
Уравнение используется в химии для определения мольной доли (концентрация, которая выражается через отношение количества молей 1 компонента к суммарному числу молей пары веществ, входящих в смесь). Кроме объёма, для газа характерна молярная масса (вес одной доли компонента) и объём. Существуют легкие способы её подсчёта:
- Стандартная. Измеряется в граммах и килограммах.
- Молекулярная. Так как газы весят мало, их вес вычисляется в специальной единице измерения — молярная масса. Для её определения суммируется вес составных атомов. Каждый компонент сравнивается с массой карбона, равной 12.
Уравнения Дальтона и Бойля
Физик и химик Дальтон считается первым учёным, предположившим структуру атомных элементов, их свойства. Общее давление вычисляется следующим образом: Р= P1 + P2 + P3. Пример: в колбе содержится по 10 г оксигена и нитрогена. Их общее Р будет равно 20 (10+10). Для вычисления pi используется температура, равная 37 градусам Цельсия.
Чтобы перевести её в градусы Кельвина, значение по Цельсию, равное 37, добавляется к 273. Результат — 310. Для вычисления количества молей газов используется масса, поделённая на молярную. Если уравнение касается нитрогена, вес каждого компонента соответствует цифре 14.
Так как вещество содержит в себе 2 атома, то 14х2, что равно 28. Масса в граммах делится на полученный результат. Таким способом вычисляется количество молей, приблизительно равное 0,4 моль. Чтобы найти аналогичное значение у оксигена, применяется масса 16. Вещество относится к двухатомным газам, поэтому 16х2 равняется 32. По результатам получается, что 0,3 моль оксигена содержится в составе газовой смеси.
Если в задаче указывается общее давление и pi в атмосферах, тогда используется в качестве константы R (0.0821 л атм/K моль). При подстановке данных в уравнение можно узнать Pобщее. Чтобы вычислить ПД нитрогена, 0,4 моль умножается на константу и температуру. Результат делится на 2 литра, что приблизительно равно 5.09 атм. Аналогичные шаги выполняются для вычисления ПД оксигена. Конечный результат равен 3.82 атм.
Свойства веществ
Значение pi газа, растворённого в жидкости, равняется pi того вещества, который образовался бы в фазе газообразования в случае равновесия с жидкостью при аналогичной температуре. Парциальное давление (ПД) измеряется в качестве термодинамической активности молекул вещества.
Газы постоянно вытекают из сферы с высоким ПД в область с низким давлением. Чем больше такая разница, тем быстрее поток. Газам свойственно растворяться, диффундировать, реагировать на ПД. В некоторых случаях показатель не зависит от концентрации газовой смеси.
При решении задач в области химии и физики учитываются свойства газов: сжимаемость и способность расширяться. Они не имеют своей формы, поэтому расширяются до заполнения сосуда, принимая его форму. По аналогичной причине они не имеют объёма. Газ давит на стенки ёмкости по всем направлениям одинаково. Характерное свойство компонентов — способность смешиваться между собой в разных соотношениях.
Так как объём зависит от температуры и давления, поэтому в норме должно быть 0 °C и 760 мм рт. ст. При этом нет места влаги. Если объём считается нормальным, его обозначают стоящей впереди буквой. Подобная зависимость отображается в термодинамике с помощью графика. Если доказана зависимость объема от давления, при этом температура постоянная, используются изотермы (линии, которые изображают на диаграмме процесс с неизменной температурой).
Точки и функции
В законе Бойля чётко указана зависимость объёма от давления при одинаковой температуре. Если данные нанести на график в функцию давления, через точки можно будет провести кривую. Точный эксперимент и незначительный разброс точек позволяют описать объёмное поведение системы с небольшой погрешностью.
Несколько подобных кривых для разных температур во всём диапазоне изученных условий позволяет описать объёмное поведение газа. Одновременно отображаются кривые постоянного давления, которые описывают изменения основных показателей. Чтобы получить окончательные результаты, кривые требуют незначительного сглаживания. Подобные графики сделать самостоятельно менее сложно.
Объём газа при неизменной температуре сильно изменяется с колебаниями давления. Но графически представить такую зависимость в широком диапазоне изменения давлений трудно. Если охвачена широкая область изменения, используются крупные масштабы.
Для упрощения процесса построения на график наносится зависимость произведения Р от давления при одной температуре, что существенно уменьшает область выявления функции. Наибольший эффект получается от применения 1−2 специальных функций объёма, которые называются коэффициентом сжимаемости и остаточным объёмом.
Каждое понятие характеризуется объёмным поведением газа с учётом его отклонений от нормального состояния вещества и созданных идеальных условий. Чтобы упростить поставленную задачу, график отображается на специальной бумаге либо при помощи компьютерных программ. Во втором случае достаточно ввести данные. Сервис самостоятельно строит прямые, кривые и прочие элементы графика.
Простые зависимости лучше отображать в стандартных программах Word. Графические сложные задачи в химии и физике решаются с помощью «Agrafer» — известная компьютерная программа, которая используется не только студентами, но и школьниками.
Источник
Секретная шпаргалка по химии. 4.2. Состав смеси газов
Команда «Газы!» была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью » Тайны задач по химии? Тяжело в учении — легко в бою!». В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я — зритель в первом ряду.
Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно — хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую «мозгобойню», чтобы вам жизнь медом не казалась. Попробуйте решить.
И.Ю. Белавин, 2005, задача 229
«Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)»
Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду «Газы!» отменять рано. Итак, поехали!
Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.
• Газовая смесь — смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.
• Объемная доля — отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.
• Мольная доля — отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.
• Плотность газа (абсолютная) — определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа — масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
• Относительная плотность газа (плотность одного газа по другому) — это отношение молярной массы данного газа к молярной массе того газа, по которому она находится
• Средняя молярная масса газа — рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей
Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль , в заданиях ЕГЭ часто встречается.
ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!
Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.
Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.
5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.
Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана
Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху
Плотность паров альдегида по метану равна 2,75. Определите альдегид
Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции — десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!
И.Ю. Белавин, 2005, задача 202
«Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)»
Задачи И.Ю. Белавина — это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: «И снова здравствуйте!», поскольку ЕГЭ с каждым годом становится «все чудесатее и чудесатее». Но это уже совсем другая история. Читайте мои статьи — и вы подстелите соломку под свою ЕГЭшную попу.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии https://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы «Решение задач по химии». Я с удовольствием вам помогу.
Репетитор по химии и биологии кбн В.Богунова
Источник
Источник
