Найти гидравлическое сопротивление кровеносного сосуда
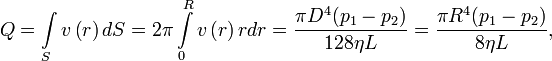
Течение Пуазейля – установившееся течение вязкой несжимаемой жидкости в тонкой цилиндрической трубке. Закон Пуазейля выполняется в сосудах с ламинарным течением крови. Q=πr4∆p/8ηl Q – объем крови, протекающий через поперечное сечение сосуда за 1 секунду ∆p – разница давлений на концах сосуда l – длина сосуда r – радиус сосуда η – вязкость (коэффициент трения) Гидравлическое давление – сила, возникающая при движении крови по сосудам. Величину обратную первой формуле называют гидравлическим сопротивлением R=8ηl/ πr4 Гидравлическое сопротивление не системы в целом, но его значительной части- большого круга кровообращения принято называть общим периферическим сопротивлением сосудов (ОПСС) и оценивается по формуле ОПСС= ,где Q- общий объём кровотока, среднее артериальное давление. Общее периферическое сопротивление сосудов- сопротивление, которое сосудистая система оказывает кровотоку. В норме ОПСС=144кПа*с/л. У сосудов наблюдается такое явление, как гипертонус: зажатость, уменьшенный радиус, уменьшение пропускной способности, отсюда происходит увеличение гидравлического сопротивления. В этих условиях для обеспечения необходимого общего объёма кровотока сердце вынуждено компенсировать рост гидравлического сопротивления ростом артериального давления. Радиус сосуда сильно влияет на гидравлическое сопротивление. Это объясняется тем, что в ламинарных потоках распределение скорости жидкости неравномерное, наибольшая скорость – в центре сосуда, т.е. основная часть объема крови переносится в центре потока. Для уменьшения гидравлического давления, необходимо расширить сосуды (увеличить радиус поперечного сечения). 51. Ламинарное и турбулентное движение жидкости. Число Рейнольдса. Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними. Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. В центре потока силы трения минимальны, и поэтому скорость крови здесь самая быстрая. По мере приближения клеток крови к стенкам сосуда сила трения увеличивается, что приводит к снижению скорости. Турбулентное (вихревое), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости. Так как частицы жидкости могут перейти из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей. Характер течения зависит от безразмерной величины, называемой числом Рейнольдса Re=ρVd/η V – средняя скорость потока, d – диметр трубы (сосуда), ρ – плотность жидкости, η – вязкость. Значение числа Рейнольдса, при котором происходит переход от ламинарного течения к турбулентному, называется критическим. Для крови Reкрит. = 970±80. При Re < Reкр. – режим течения ламинарный. При Re > Reкр. – турбулентный. Разрушителями ламинарного движения могут оказаться резкие изломы, выступы в сосуде. 52. Пульсовая волна и скорость ее распространения. Формула Моенса-Кортевега. Пульсовая волна – распространяющаяся по аорте и артериям волна повышенного (над атмосферным) давления, вызванная выбросом крови из левого желудочка в период систолы. Пульсовая волна распространяется со скоростью vп = 5-10 м/с. Величина скорости в крупных сосудах зависит от их размеров и механических свойств ткани стенок: где Е – модуль упругости, h – толщина стенки сосуда, d – диаметр сосуда, ρ – плотность вещества. С возрастом, по мере уменьшения эластичности сосудов, растет модуль упругости Е, что отслеживается ростом скорости распространения пульсовой волны.53. Внутреннее трение в жидкости. Уравнение Ньютона. Вязкость крови. Основные факторы, влияющие на вязкость крови в организме. Свойство жидкостей, которое мы называем вязкостью, проявляется в том, что всякое движение, возбуждаемое в жидкости, вскоре прекращается. Вязкость жидкости можно обнаружить и изучать количественно, рассматривая взаимодействие слоев жидкости, имеющих различную скорость. Экспериментально установлено, что сила трения, возникающая между слоями 1 и 2: здесь – отношение, называемое градиентом скорости в направлении, перпендикулярном потоку жидкости. S – площадь соприкосновения слоев;n- коэффициент пропорциональности, зависящий от свойств жидкости, и называемый динамическим коэффициентом вязкости. Уравнение (4) можно сформулировать так: сила вязкого трения пропорциональна градиенту скорости в направлении, перпендикулярном потоку, и площади соприкосновения слоев, с коэффициентом пропорциональности – коэффициентом вязкости жидкости. Взаимодействие между слоями осуществляется возникающими парами сил. Любая из них соответствует уравнению (4). Эта пара сил действует так, чтобы способствовать выравниванию скоростей в слоях. Если в формуле (4) все величины будут иметь размерность основных единиц системы СИ, то единица вязкости h будет иметь размерность 1 Па×с. У различных жидкостей коэффициент вязкости различен. У ньютоновских жидкостей коэффициент вязкости зависит только от их температуры. У неньютоновских – коэффициент вязкости зависит не только от температуры, но и от условий протекания: градиента скорости, размеров потока, давления в нем. Ньютоновские жидкости имеют простые молекулы, или это молекулы низкомолекулярных органических соединений. К неньютоновским относятся жидкости с протяженными молекулами высокополимеров, суспензии, эмульсии. Кровь – неньютоновская жидкость, представляющая собой суспензию форменных элементов в белковом «растворителе» – плазме. Форменные элементы – эритроциты, лейкоциты, тромбоциты – составляют сообща 40-50% объема крови. Поэтому если вязкость плазмы – порядка 1,7 – 2,2 мПа×с, то вязкость крови в норме – 4 – 5 мПа×с. При движении крови в спокойном (ламинарном) потоке эритроциты выстраиваются своей длинной осью вдоль потока. В неспокойном потоке такой строй эритроцитов нарушается, меняется и коэффициент вязкости. Значения коэффициента вязкости крови в норме и при патологии могут отличаться в несколько раз. Если в номе это 4 – 5 мПа×с, то при отклонениях от нормы – это диапазон от 1,5 до 24 мПа×с. Следовательно, коэффициент вязкости может быть важным диагностическим показателем ее состояния. 54. Измерение артериального давления по методу Короткова.Для измерения давления крови в клинике применяется бескровный метод, предложенный более ста лет назад сотрудником Военно-Медицинской академии Н.С. Коротковым. Он заключается в том, что измеряют минимальное давление, которое необходимо приложить снаружи, чтобы сжать артерию до прекращения в ней кровотока. Это давление близко к давлению крови в артерии. При этом большое значение имеет выслушивание звуков, возникающих при прохождении крови через сжатую манжетой артерию. Прибор для измерения артериального давления по этому методу состоит из манжеты, нагнетателя (груши) и манометра. Для прослушивания звуков используется фонендоскоп. Манжета закрепляется в зоне плечевой артерии пациента, т.е. на уровне сердца пациента в его сидячем или лежачем положении. Фонендоскоп устанавливается в зоне локтевого сгиба. При закрытом выпускном клапане, в манжету нагнетают воздух, ритмически сжимая и отпуская грушу. Давление в манжете контролируется по манометру. Первоначально в манжете создается давление, на 10-20 мм рт. столба выше того, при котором перестает прослушиваться пульс на плечевой артерии. При полностью сжатой артерии никаких звуков через фонендоскоп не прослушивается. Затем, медленно открывая выпускной клапан, добиваются плавного снижения давления воздуха в манжете. При некотором давлении в манжете, работающее сердце оказывается в состоянии толчками проталкивать кровь через артерию. Начинают прослушиваться отчетливые тоны, называемые начальными. В этот момент времени показания манометра соответствуют максимальному, или систолическому давлению. Прослушиваемые при этом звуки обусловлены вибрацией стенок артерии при прохождении пульсовой волны. При дальнейшем снижении давления в манжете, начальные тоны дополняются шумами, которые обусловлены турбулентным течением крови в частично сдавленной артерии. По мере распрямления стенок артерии и восстановления ее нормального просвета, турбулентные шумы стихают и в фонендоскопе вновь прослушиваются только тоны, называемые последовательными. Эти тоны быстро ослабевают, и затем звуковые явления полностью прекращаются. В этот момент просвет артерии полностью восстановился, и в ней устанавливается ламинарное движение крови. Показания манометра в момент окончательного исчезновения как турбулентных шумов, так и последовательных тонов, соответствуют минимальному, или диастолическому давлению крови.55. Типы кровеносных сосудов, их функции. Характер движения крови в сосудах различного типаКровеносные сосуды по своим свойствам и функциям подразделяются на четыре типа: артерии эластичного типа, артерии мышечного типа, капилляры и вены. Артерии эластичного типа можно назвать аккумуляторами давления крови: благодаря им поддерживается непрерывный ток крови во время диастолы, когда сердце отдыхает. Стенки таких сосудов содержат значительное количество эластических волокон, благодаря чему в ходе функционирования артерий этого типа их радиус способен при упругих деформациях увеличиваться в 1,1 раза (на 10%), что соответствует увеличению площади сечения на 20%. Наряду с эластичными волокнами, стенки сосудов данного типа имеют значительное количество коллагеновых волокон, природное предназначение которых – обеспечение прочности тканей. Артерии мышечного типа, меняя тонус, меняют распределение давления крови по органам и тканям.Aртериолы. Изменения тонуса в отдельных звеньях системы артериол обеспечивают повышенный кровоток в тех органах, которые в данный момент в этом нуждаются, как в связи с физическими нагрузками, так и в ходе регулирования теплообмена организма с окружающей средой. Cистема артериол передает пульсовую волну, которая окончательно затухает лишь на входе в капилляры. Примеры системных нарушений в работе этого участка кровеносной системы – гипертония и гипотония. Капилляры. Гидравлическое сопротивление всей системы капилляров невелико: если на входе в капилляры давление крови 20-40 мм рт.ст., то на выходе – 8-15 мм рт.ст., и это несмотря на впечатляющую суммарную их протяженность. Объяснение тому – очень малая скорость движения крови в этих сосудах: порядка 0,5 мм/с. Вены – сложная разветвленная сеть сосудов, замыкающая выход капилляров с предсердиями. Эта система работает в условиях низкого давления; оно достигает нулевой отметки, и даже, как уже говорилось, может быть отрицательным. В этих условиях, в правом предсердии возникает еще более низкое давление, чтобы всасывать кровь, если она поступает слабо.56. Общая характеристика опорно-двигательного аппарата (ОДА). Число степеней свободы суставов и ОДА.Опорно-двигательный аппарат (ОДА) человека состоит из двух частей: пассивной и активной. Пассивная часть ОДА содержит следующие элементы: -кости скелета -соединения костей (Биомеханика ОДА рассматривает в основном прерывные соединения костей – суставы). -связки Активная часть ОДА содержит следующие элементы: -скелетные мышцы . -Двигательные нервные клетки (мотонейроны). -Рецепторы ОДА. -Чувствительные нейроны (афферентные нейроны). Биомеханическими функциями ОДА являются: -опорная – обеспечивает опору для мягких тканей и органов, а также удержание вышележащих сегментов тела; -локомоторная (двигательная) – обеспечивает перемещение тела человека в пространстве; -защитная – защищает внутренние органы от повреждений. Сустав- элемент ОДА, обеспечивающий соединение костных звеньев и создающий подвижность костей друг относительно друга. Суставы являются наиболее совершенными видами соединения костей. У человека их около 200. Число степеней свободы – число независимых видов поворота в суставе Опорно-двигательный аппарат человека с позиции теории машин и механизмов, можно рассматривать как сложный биомеханизм, состоящий из жестких звеньев (костей) и кинематических пар определенных классов (суставов). С этой точки зрения различают: Одноосные суставы. Движения в них происходят только вокруг одной оси. Эти суставы обладают одной степенью свободы. В организме человека таких суставов насчитывается 85. Двуосные суставы. Движения в них происходят вокруг двух осей. Эти суставы обладают двумя степенями свободы. В организме человека 33 двуосных сустава. Многоосные суставы. Движения в них происходят вокруг трех осей. Эти суставы обладают тремя степенями свободы. В организме человека таких суставов 29. Для определения числа степеней свободы ОДА человека применяют формулу Сомова-Малышева. Число степеней свободы для модели тела человека с 148 подвижными звеньями составляет: n = 6 × 148 – 5 × 85 – 4 × 33 – 3 × 29 = 244. Это означает, что для описания положения модели тела человека в каждый момент времени необходимо иметь 244 уравнения. Для количественных оценок параметров движения важно знать положение мгновенных осей вращения в суставе, так как это влияет на значение плеч сил отдельных мышц. Мгновенные оси вращения в суставах могут смещаться. Это происходит из-за того, что в суставах могут осуществляться три типа движения сочленяющихся поверхностей: скольжение, сдвиг и качение. Возможность таких движений обусловлена тем, что соприкасающиеся суставные поверхности не тождественны по форме. Под влиянием занятий спортом адаптация суставов ОДА происходит разнонаправленно: в одних суставах подвижность увеличивается, в других – уменьшается. Так, у велосипедистов наибольшая подвижность отмечается в голеностопном суставе и наименьшая – в тазобедренном и плечевом57. Особенности работы мышц в сочленении с костями.Опорно-двигательный аппарат является системой рычагов. Рычагом называется твёрдое тело, способное совершать вращательные движения около оси, на плечи которого действуют 2 противоположные силы: движущая (мышечные сокращения) и сила сопротивления. В зависимости от величины движущей силы и силы сопротивления возможно равновесие или движение рычага.Плечо силы-кратчайшее расстояние между линией приложения силы и центром вращения. Момент силы-произведение силы на плечо. Измеряется в Н х м Большинство мышц крепятся вблизи суставов и подходят к костям под острым углом,при этом плечо силы меньше плеча сопротивления (при таком прикреплении мышцы проигрывают в силе). Но существуют образования, способствующие увеличению плеча силы мышц: сесамовидные кости,блоки,отростки,бугорки,шероховатости, выступы. За счет этих образований увеличивается момент силы. Следовательно, сила мышц существенно зависит от плеча рычага.58. Виды деформации. Закон Гука. Коэффициент жесткости. Модуль упругости. Особые свойства костной ткани.Если приложить к предмету внешнюю силу F, то это изменит расположение частиц тела. Эти частицы, соответственно, будут стремиться вернуться в прежнее положение. Таким образом, возникает сила упругости. Если сила упругости меньше внешней силы, то возникает деформация.Виды деформации: сжатие, растяжение, скручивание, сдвиг, изгибание.Закон Гука:F=kx, где х-абсолютная деформация, k-коэффициент жесткости.Коэффициент жесткости зависит от свойств материала и геометрии предмета.Особые свойства костной ткани: 1.Сочетание минеральных и органических компонентов.3.Трубчатые кости легче, чем сплошные той же прочности.4. Обновляется за счет остеокластов и остеобластов.5.Расширение в области суставов обеспечивает прочность кости. Рекомендуемые страницы:
|
Источник
Уравнение Пуазёйля – закон, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения.
Согласно закону, секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиентудавления в трубе) и четвёртой степени радиуса (диаметра) трубы:
Где Q – объемный секундный расход жидкости; R – радиус трубопровода; p1-p2- перепад давлений на трубке; n-коэффициент трения; L- длина трубки.
Закон Пуазёйля работает только при ламинарном течениии при условии, что длина трубки превышает так называемую длину начального участка, необходимую для развитияламинарного теченияв трубке.
Гидравлическое сопротивление прямо пропорционально длине сосуда и вязкости крови и обратно пропорционально радиусу сосуда в 4-й степени, то есть больше всего зависит от просвета сосуда , а также от состояния стенок сосудов и от их эластичности.
Так как наибольшим сопротивлением обладаютартериолы,общее периферическое сопротивление сосудов(ОПСС)зависит главным образом от их тонуса.Различают центральные механизмы регуляции тонуса артериол (нервные и гормональные влияния) и местные (миогенная , метаболическая и эндотелиальная регуляция).
На артериолы оказывают постоянный тонический сосудосуживающий эффектсимпатические нервы. Основные гормоны, в норме участвующие в регуляции тонуса артериол, – этоадреналини норадреналин.
Миогенная регуляция сводится к сокращению или расслаблению гладких мышц сосудов в ответ на изменения трансмурального давления; при этом напряжение в их стенке остается постоянным. Тем самым обеспечивается ауторегуляция местного кровотока – постоянство кровотока при меняющемся перфузионном давлении.
Метаболическая регуляция обеспечивает расширение сосудов приповышении основного обмена(за счет выбросааденозинаипростагландинов) игипоксии(также за счет выделения простагландинов).
7. Законы движения жидкости. Уравнение неразрывности; его связь с особенностями системы капилляров. Уравнение Бернулли; его связь с кровоснабжением мозга и нижних конечностей.
Для движения жидкости по сосудам необходима энергия, создающая давление.
Жидкость двигается из мест с большим давлением в места с меньшим давлением.
Скорость течения жидкости зависит от суммарного поперечного сечения сосудов.
Чем меньше суммарное поперечное движение сосудов, тем больше скорость течения жидкости.
Один и тот же объем жидкости проходит с большей скоростью более узкие участки, чем более широкие.
Следствим несжимаемости жидкости является ее свойство: чем уже русло, тем больше
скорсть течения. Это свойство описывается:
Уравнением неразрывности: S1V1= S2V2, или SV=Const
Здесь S-площадь поперечного сечения потока,V-средняя скорость жидкости в этом сечении.
В спокойном состоянии человека скорость кровотока в аорте – порядка V1=0,4м/с.Скорость в капиллярах- V2=0,5 мм/c.Разница значений примерно в 800 раз. Следовательно, если площадь сечения аорты S1=4см2,то общая площадь поперечных сечений капилляров большого и малого кругов кровообращения составляет S2=3200см2.
Оценим степень ветвления общего потока крови в системе капилляров.Диаметр капилляра d=10мкм=10 -3 см. Следовательно,площадь его сечения S=пd 2/4=0,78*10см 2. Таким образом,кровь из аорты разветвляется в системе капилляров на N=S2/s=3,2*103/0,78*10 -6=4,1*10 9 штук.
Уравнение Бернуллисоответствует закону сохранения механической энергии при движении жидкости или газа и верно в той степени, в которой потери на трение малы. Оно имеет следующий вид:=const
Здесь p0- полное давление. Величинаp- это давление, которое поток оказывает на стенки; его называют статическим давлением. СлагаемоеpV2/2 называется динамическим давлением.Слагаемоеpghсоответствует тому вкладу в общее давлениеp0, которое создается участками потока, приподнятыми на высотуh, если таковые имеются.p- плотность жидкости;V- ее скорость.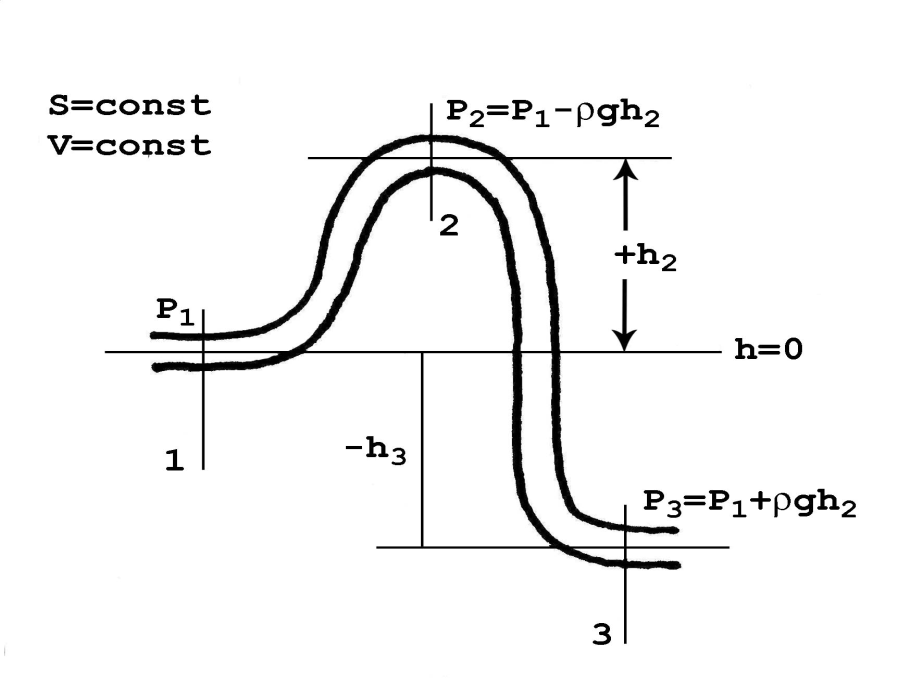
статическое давление в приподнятых участках: p2 <p1, а в опущенных – наоборот,p3 >p1.
Применительно к системе кровообращения, если p1- давление, создаваемое сердцем, работающим на высотеh= 0, то все, что находится выше этого уровня, имеет пониженное давление (а это,в частности, мозг), а все, что ниже (ноги,например) – давление выше, чем то, которое создает работающее сердце. Для мозга слагаемоеpghимеет величину порядка -30 мм рт. столба, а для ног – порядка +110 мм рт. столба. Система кровообращения имеет механизмы регулирования, вносящие поправки на снабжение кровью органов, находящихся в неравных условиях.
_______________________________________________________________________________________
Соседние файлы в предмете Медицинская физика
- #
- #
- #
- #
- #
Источник

