Найти объем сосуда в котором при нормальном давлении
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости. Любой многоугольник имеет свою площадь.
В качестве единицы измерения площади принято брать квадрат со стороной, равной единице. В случае объёма за единицу измерения берут куб с ребром, равным единице. Этот куб называют кубическим сантиметром (метром, миллиметром и т. д.) и обозначают $1 см^3$ (соответственно, $1 м^3, 1 мм^3$ и т.п.).
Другую аналогию между площадью и объёмом можно провести в самой процедуре их измерения. Объём выражается положительным числом, показывающим количество единиц измерения объёмов и частей, которые укладываются в данном теле. Число единиц объёма тела зависит от выбранной единицы измерения, то есть меняется в зависимости от того, выбраны $cм^3, м^3$ и т.п. Единицу измерения традиционно указывают после числа.
Приведём простейший пример. $V=3 мм^3$ – эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник – это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер – вершинами.
- Призма – это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).
Нахождение объёма параллелепипеда
Параллелепипед – это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания – параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания – прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда – это длины трёх рёбер с общей вершиной. В речи мы называем измерениями “длину”, “ширину” и “высоту” (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида – это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр – некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус – это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=frac{Sh}{3}$.
Нахождение объёма шара
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на равном расстоянии (радиусе) от данной точки (центра).
Рисунок 4. Сфера. Автор24 — интернет-биржа студенческих работ
Шар – это некоторое тело (сосуд), которое ограничено сферой. Другой вариант определения: шар – это тело (сосуд), полученное в результате вращения полукруга вокруг диаметра этого полукруга.
Рисунок 5. Шар. Автор24 — интернет-биржа студенческих работ
Определение 5
Объём шара: $V=frac{4}{3}pi R^3$, где $R$ – радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Источник
Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):
V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.
По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:
Ответ: V2 = 746мл.
Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:
Обозначив искомое давление газа через Р2, можно записать:
Ответ: Р2 = 304кПа (2280мм.рт.ст.).
Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:
По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.
Подставляя эти значения в уравнение, находим:
Ответ: Газ нужно нагреть на 2730С.
Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 4,8л
Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 82,3кПа.
Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:
Ответ: V = 769, 07 мл.
Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 106,3кПа.
Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 1,97м3.
Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:
Ответ: Т2 = 1980С.
Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:
<
Ответ: V0 = 542,3мл.
Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:
где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,
получим:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:
Ответ: mЭ(Ме) = 39,4г/моль.
Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).
Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:
Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.
Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.
Ответ: а); б).
Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.
Ответ: б); в).
Источник
Молекулы вступают в реакцию в определённых соотношениях, и это описывают химические реакции. Например, из этого уравнения
2Н2 + О2 = 2Н2О
видно, что в реакции приняли участие 2 молекулы водорода и 1 молекула кислорода, образовав при этом 2 молекулы воды. Но молекула так малы, что увидеть их невозможно, и уж тем более нельзя взять их в руки. Поэтому в учебнике химии и появляется понятие моль – количество вещества, в котором содержится число Авогадро частиц (6,02*10 в двадцать третьей степени). Рядом с этим понятием стоит другое – молярная масса, то есть масса 1 моля частиц. Молярная масса совпадает с атомной или молекулярной, рассчитывается по таблице Менделеева и выражается в граммах на моль (г/моль).
Фото: pixabay.com
Но мы прекрасно знаем, что не все вещества в обычных условиях находятся в твёрдом или жидком состоянии. Например, кислород, азот, хлор, неон – это газы. Резонно спросить: а как же их взвешивать? На этот случай химии для 8 класса припасено ещё одно понятие – молярный объём.
Что такое молярный объём
Тут следует запомнить, что в обычных условиях 1 моль любого газа занимает одинаковый объём. То есть молярный объём – это объём 1 моля любого газа. Сейчас советую на всякий случай вспомнить, что в 1 моле любого вещества (в том числе газа) содержится число Авогадро частиц. Старайтесь не забывать об этом факте.
Теперь надо обязательно упомянуть следующее. Все знают, что при изменении температуры и давления объём газов меняется. Так вот чтобы все расчёты вести правильно, то есть в одинаковых условиях, говорят о нормальных условиях: температуре 0 градусов Цельсия и давлении в 1 атмосферу (или 101,3 кПа). Это нужно просто запомнить:
нормальные условия в химии: температура – 0 градусов Цельсия, давление – 1 атм.
Экспериментально было доказано, что в нормальные условиях 1 моль любого газа занимает объем 22,4 литра.
То есть молярный объём любого газа в н.у. составляет 22,4 л/моль.
И это число тоже нужно запомнить! Оно даже важнее, чем сами нормальные условия, потому используется это число в решениях по химии намного чаще, чем н.у. (нормальные условия).
Как найти молярный объём
Очень просто. Если молярную массу для каждого вещества нужно рассчитывать по таблице Менделеева, то
молярный объём для всех газов одинаков.
Пример 1.
Молярная масса воды Н2О 18 г/моль (2*1+16, всё берем из периодической таблицы), молярная масса оксида кальция СаО 56 г/моль (40+16), молярная масса серной кислоты Н2SO4 98 г/моль (2*1+32+4*16).
Зато в нормальных условиях молярный объём кислорода О2 22,4 л/моль, молярный объём фтора P2 22,4 л/моль, молярный объём ксенона 22,4 г/моль. Приятно, не правда ли?
Другое дело, если речь идёт о химических реакциях. Но для начала просто потренируемся с цифрами.
Пример 2.
Определите объём, который занимают 10 моль кислорода в н.у.
Решение:
Молярный объём кислорода 22,4 л/моль, то есть 1 моль занимает 22,4 л. Следовательно, 10 моль будут занимать в 10 раз больше 22,4*10=224 литра. Это и есть ответ: 10 моль кислорода займут объём 224 литра.
Пример 3.
Известно, что неон в н.у. занял объём 5,6 литра. В каком количестве взят неон (в молях)?
Решение:
1 моль занимает объём 22,4 литра, а вот неизвестное число моль заняло объём 5,6 литра. Можно составить пропорцию:
1 моль – 22,4 литра
Х моль – 5,6 литра
Отсюда Х=1*5,6/22,4=0,25. Значит ответ такой: неон взяли в количестве 0,25 моль.
Пример 4.
Это уже расчёт по химической реакции, поэтому будьте внимательны. Итак, хлор прореагировал с водородом с образованием хлорида водорода:
Н2 + Cl2 = 2HCl
Для реакции взяли 11,2 литра водорода. Сколько понадобилось хлора (н.у.)?
Решение:
Посмотрим, сколько нам дано водорода по условию задачи. 1 моль водорода занимает объём 22,4 литра. Но у нас всего 11,2 литра водорода, то есть Х моль. Составим пропорцию:
1 моль – 22,4 литра
Х моль – 11,2 литра
Отсюда Х=1*11,2/22,4=0,5 моль водорода. Значит, по условию задачи у нас водорода 0,5 моль.
Из уравнения химической реакции Н2 + Cl2 = 2HCl видно, что нам нужно по 1 молю водорода и хлора (об этом говорят коэффициенты в уравнении). То есть, 1 моль водорода реагирует с 1 молем хлора. Но нам дали всего 0,5 моль водорода, сколько нам нужно хлора? Составим ещё одну пропорцию:
1 моль водорода реагирует с 1 молем хлора
0,5 моль водорода реагирует с Х молями хлора.
Отсюда получаем: Х=0,5*1/1=0,5 моль. Таким образом, нам нужно 0,5 моль хлора. А это количество занимает объём 22,4*0,5=11,2 литра.
Ответ: понадобилось 11,2 литра хлора.
В следующий раз мы научимся делать расчёты по реакциям, в которых участвуют и твёрдые вещества, и газы, то есть одновременно будем использовать молярную массу и молярный объём.
Пишите, пожалуйста, в комментариях, что осталось непонятным, и я обязательно дам дополнительные пояснения. Жалуйтесь на сложности в изучении школьного курса и говорите, что вас испугало в учебнике химии. И тогда следующая статья будет рассказывать именно об этой проблеме.
Источник
Задача 62.
Вычислить массу: а) 2л Н2 при 15 °С и давлении 100,7кПа (755мм рт. ст.); 6) 1м3 N2 при 10 °С и давлении 102,9 кПа (772мм рт. ст.); в) 0,5 м3 Cl2 при 20 °С и давлении 99,9 кПа (749,3мм рт. ст.).
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где P и V – давление и объём газа при температуре T; P0 (101,325кПа) и V0 – давление и объём газа при нормальных условиях; T0 (273К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газов при нормальных условиях:
Рассчитаем массу каждого газа, учитывая, что мольный объём газа равен 22,4л и, зная молекулярную массу газов, получим:
Ответ: а) 0,168г; б) 1.23кг; в) 1,456кг.
Задача 63.
Определить объем, занимаемый 0,07кг N2 при 21°С и давлении 142 кПа (106 мм рт. ст.).
Решение:
Зная мольный объём и мольную массу азота (28г/моль), находим объём, который будет занимать 0,07кг (70г) азота при нормальных условиях:
Затем приведём полученный объём к температуре Т = 21оС (294К) и Р = 142кПа, используя выражение, объединяющее законы Гей-Люссака и Бойля-Мариотта:
где P и V – давление и объём газа при температуре T; P0 (101,325кПа) и V0 – давление и объём газа при нормальных условиях; (273 К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газа при заданной температуре
Ответ: 43л.
Задача 64.
Бертолетова соль при нагревании разлагается с образованием КСI и О2. Сколько литров кислорода при 0 °С и давлении 101,3 кПа можно получить из 1 моля КСIО3?
Решение:
Уравнение реакции термического разложения бертолетовой соли имеет вид:
Из уравнения реакции следует, что из двух молей бертолетовой соли образуется три моля кислорода, т.е. из одного моля соли образуется полтора моля кислорода (2:3 = 1:х; x = 1.3/2 = 1,5моль).
Объём кислорода при нормальных условиях (T0 =0 °С и P0 =101.325кПа) можно рассчитать по формуле:
V(B) – объём газа, л;
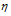(B) – количество газа, моль;
V(M) – мольный объём, 22,4л.
Тогда
V(кислорода) = 1,5 . 22,4 = 33,6л.
Ответ: 33,6л.
Задача 65.
Сколько молей содержится в 1м3 любого газа при нормальных условиях?
Решение:
Зная, что один моль любого газа при нормальных условиях (Т0 =0 °С и Р0 =101.325 кПа) занимает 22,4л, рассчитаем количество молей газа в 1м3 (1000 л) из пропорции:
Ответ: 44,64моль.
Задача 66.
Чему равно атмосферное давление на вершине Казбека, если при 0 °С масса 1л взятого там воздуха равна 700 мг?
Решение:
Мольная масса воздуха равна 29 г/моль. Нормальными условиями для газов являются температура 0 °С и давление 101,325 кПа (760 мм рт ст.). Масса одного литра воздуха при нормальных условиях равна 1296,64 мг:
Теперь рассчитаем атмосферное давление на вершине Казбека из пропорции:
Ответ: 54,7к Па (410,3 мм рт. ст.).
Задача 67.
При взаимодействии одного объема СО и одного объема Сl2 образуется один объем фосгена. Установить формулу фосгена.
Решение:
По условию задачи выходит, что из молекулы угарного газа и одной молекулы хлора образуется одна молекула фосгена. Так как молекула угарного газа СО состоит из одного атома углерода и одного атома кислорода, а молекула хлора Cl2 состоит из двух атомов хлора, то, следовательно, молекула фосгена будет состоять из одного атома углерода, одного атома кислорода и двух атомов хлора. Тогда формула фосгена будет иметь вид: CCl2O.
Уравнение реакции будет иметь вид:
СО + Cl2 → ССl2O.
Ответ: ССl2O.
Задача 68.
Какой объем СО2 получается при сгорании 2л бутана? Объемы обоих газов измерены при одинаковых условиях.
Решение:
Уравнение реакции горения бутана имеет вид:
2С4Н10 + 13О2 = 8СО2 + 10Н2О
Из уравнения реакции следует, что при сгорании одного моля бутана образуется четыре моля углекислого газа. Известно, что при одинаковых условиях одинаковое количество газов занимают одинаковый объём. Один моль любого газа при нормальных условиях занимает объём в 22,4 л.
Исходя, из этих утверждений рассчитаем объём выделившегося углекислого газа при сгорании 2 л бутана, составив пропорцию:
Ответ: 8л.
Задача 69.
В замкнутом сосуде при 120°С и давлении 600 кПа находится смесь, состоящая из трех объемов О2 и одного объема СН4. Каково будет давление в сосуде, если взорвать смесь и привести содержимое сосуда к первоначальной температуре?
Решение:
Уравнение реакции имеет вид:
CH4 + 2O2 → CO2 + 2H2O
Из уравнения реакции следует, что из одной молекулы метана и двух молекул кислорода образуются одна молекула углекислого газа и две молекулы воды, т. е. реакция протекает без изменения объёма. Начальный объём системы состоял из одного объёма метана и трёх объёмов кислорода, после реакции в системе остался один объём не прореагировавшего кислорода и три объёма продуктов реакции (один объём метана и два объёма паров воды). Поскольку реакция протекает без изменения объёма, а по окончании реакции содержимое сосуда приводится к первоначальной температуре, а общее число молекул газов не изменилось, то давление в системе останется прежним, т. е. 600 кПа.
Ответ: не изменится.
Задача 70. После взрыва 0,020 л смеси водорода с кислородом осталось 0,0032 л кислорода. Выразить в процентах по объему первоначальный состав смеси.
Решение:
Находим объём газов, вступивших в реакцию:
0,020 – 0,0032 = 0,0168 л.
Уравнение реакции горения водорода имеет вид:
2Н2 + О2 = 2Н2О
При взаимодействии водорода с кислородом из двух молекул водорода и одной молекулы кислорода получаются две молекулы воды, следовательно, из трёх молекул образовавшихся газов одна молекула будет принадлежать кислороду. Таким образом, объём кислорода, вступившего в реакцию, будет составлять одну треть объёма смеси газов – продуктов реакции. Отсюда количество кислорода, вступившего в реакцию, составляет 0,00565 л (0 0168/3 = 0,0056).
Следовательно, общее количество кислорода до реакции составляло 0,0088л (0,0056 + 0,0032 = 0,0088).
Тогда содержимое водорода до реакции составляло 0,0112л (0,02 – 0,0088 = 0.0112).
Рассчитаем в процентах первоначальный состав газовой смеси:
Ответ: 56%Н2; 44%О2.
Источник