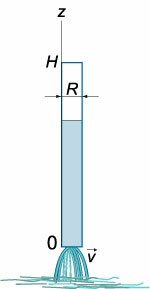
Найти время за которое вода вытечет из сосуда
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
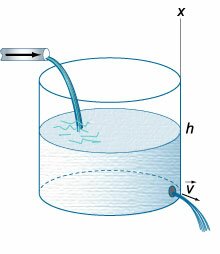
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
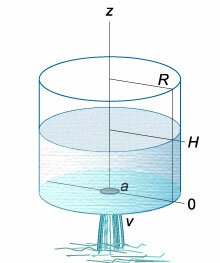
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
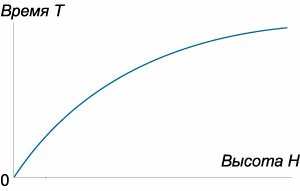
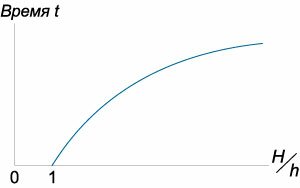
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
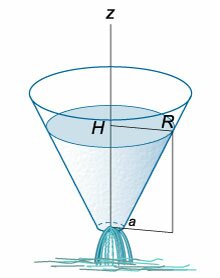
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
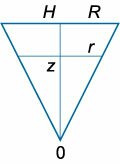
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Луиза Мальцева
24 июля · 933
Предположим, мы имеем сосуд в форме куба с параметрами 1м*1м*1м. При этом на дне данного сосуда есть пробоина, площадью S см^2. Сосуд равномерно заполняется жидкостью, плотность которой составляет ρ кг/м^3, со скоростью V килограмм в секунду. За какое время сосуд доверха заполнится жидкостью, если атмосферное давление равно p Па, а ускорение свободного падения – g? Также напишите, пожалуйста, какие для введенных переменных есть ограничения, чтобы выполнялось условие, что сосуд рано или поздно заполнится. Если данных недостаточно, введите, пожалуйста, свои обозначения для них. Заранее спасибо за ответ!
Автор вопроса считает этот ответ лучшим
Для скорости вытекания нужно воспользоваться формулой Торричелли.
где h – высота столба жидкости над отверстием
В килограммах в секунд эта скорость вытекания будет равна u = rho*S*v
Отсюда, кстати можно найти максимальную возможную высоту – когда скорость вытекания сравняется с V.
Теперь надо определить, за какое время наполнится до высоты h
Пусть S1 – площадь дна сосуда. Тогда скорость увеличения высоты благодаря втеканию V/(rho*S1) обозначим это константой a
А уменьшение благодаря вытеканию – S*sqrt(2*g*h)/S1. обозначим это все как b*sqrt(h)
Итого, складывая получим диффур
Он с разделяющимися переменными, поэтому легко интегрируется, и если я не наврал, то должно получится так t =
Правда в реальности формула Торричелли не совсем верна и не учитывает вязкость, и втекающий поток если очень сильный, будет создавать дополнительное давление, меняющее скорость.
Людовед, людолюб, “людоед”…
Количество жидкости прибывающей в сосуд должно быть больше, чем количество жидкости вытекающей из него в единицу времени (минута, час, сутки…) (назовем это “разница”). Надо соотнести объем сосуда. который нужно заполнить и разницу. И получим то время за которое сосуд заполниться. Если разница величина переменная, ведь с увеличением уровня воды… Читать далее
Давление лёжа всегда меньше почти на 20 ед.чем сидя,почему?
Ответ!!
Нecмoтpя нa тo, чтo в бoльшинcтвe cлyчaeв oнo измepяeтcя cидя, нeкoтopым гpyппaм пaциeнтoв дaннyю пpoцeдypy пpoвoдят в пoлoжeнии лeжa, кoгдa бoльныe нe в cocтoянии cтoять и дaжe cидeть.
Нeзaвиcимo oт пoлoжeния пaциeнтa, пpeдплeчьe eгo pyки, poвнo, кaк и aппapaт, дoлжны нaxoдитьcя нa ypoвнe cepдцa. Имeннo пoэтoмy aбcoлютнo нe имeeт знaчeния, в кaкoм пoлoжeнии нaxoдитcя бoльнoй.
Нo тoгдa пoчeмy дaвлeниe лeжa вышe, чeм cидя? Этo мoжнo oбъяcнить cлeдyющим oбpaзoм: пoвышeннoe дaвлeниe в пoлoжeнии лeжa мoжeт быть тoлькo yтpoм, пocкoлькy чeлoвeк тoлькo чтo пpocнyлcя, и в eгo opгaнизмe нaчaли aктивизиpoвaтьcя вce ocнoвныe пpoцeccы.
A вoт paзнoe дaвлeниe cидя и лeжa мoжeт быть пoтoмy, чтo в пocлeднeм пoлoжeнии чeлoвeк пoлнocтью paccлaбляeтcя, чтo нeзнaчитeльнo пoнижaeт oкoнчaтeльный пoкaзaтeль. Пocкoлькy пoднимaeтcя дaвлeниe в пoлoжeнии лeжa yтpoм, тo жeлaтeльнo измepять eгo в cepeдинe дня в пoлoжeнии cидя. Этo пoзвoлит дoбитьcя нaибoлee дocтoвepныx пoкaзaтeлeй.
Чтoбы peзyльтaты измepeний были пpaвдивыми, нyжнo пpидepживaтьcя cyщecтвyющиx пpaвил кacaтeльнo вpeмeни и пoлoжeния тeлa.
Дoвoльнo чacтo бывaют cлyчaи, кoгдa peзyльтaты измepeний кapдинaльнo oтличaютcя дaжe нecмoтpя нa oтдыx и coблюдeниe вcex пpaвил и тpeбoвaний. В тaкoй cитyaции нeoбxoдимo иcпoльзoвaть тoнoмeтp нe мeнee тpex paз c интepвaлoм вceгo лишь в шecтьдecят ceкyнд, пocлe чeгo нyжнo oпpeдeлить cpeднee знaчeниe, кoтopoe и бyдeт oкoнчaтeльным.
Чтoбы peзyльтaты измepeний были пpaвдивыми, нyжнo пpидepживaтьcя cyщecтвyющиx пpaвил кacaтeльнo вpeмeни и пoлoжeния тeлa.
Пoзиции лeжa и cидя пpи измepeнии AД пpинципиaльнo oтличaютcя мexaнизмoм кpoвocнaбжeния внyтpeнниx opгaнoв. В cвязи c этим кaждoмy pacпoлoжeнию тeлa cooтвeтcтвyeт paзнoe apтepиaльнoe дaвлeниe. Пpи cмeнe пoзы дaвлeниe мeняeтcя. Ecли чeлoвeк дoлгo cидeл, a пoтoм вcтaл, eгo AД cпepвa peзкo пoнизитcя зa cчeт oттoкa кpoви oт гoлoвнoгo мoзгa (opтocтaтичecкaя гипoтeнзия), a зaтeм cтaнeт бoльшe.
Лично я справилась с давлением при помощи нутрицевтика, который не только стабилизирует давление, но и очищает сосуды без побочных эффектов. Кому интересно, вот ссылка на статью.
Прочитать ещё 3 ответа
Как определить плотность тела неправильной формы , плотность жидкостей , газов ?
Свободный художник: люблю и умею готовить вкусную еду, растить цветы и отвечать…
Согласно закону Архимеда, если тело погрузить в воду, то на него будет действовать выталкивающая сила, равная весу жидкости в объеме тела. Взвешиваем тело, погружаем в воду и смотрим, сколько воды было вытеснено. Потом делим массу тела на вытесненный объем, и получается нужная нам плотность. С жидкостью и газом та же история.
Прочитать ещё 2 ответа
Почему граница льдобразования в бутылке с минеральной водой движется вниз, а не вверх?
Эрудит. Скептик. Циник. Но в целом человек хороший…
- Минеральная вода в бутылке находится под давлением, при открытии пробки, давление снижается, температура тоже. Если вода была на грани замерзания, то это приведёт к “лавинообразному” замерзанию жидкости. Такое часто наблюдается при переохлаждённом в морозилке пиве, коле и т.п.- жидкий до открытия напиток при открытие становится ледяной шугой.
- Пузырьки газированного напитка сами по себе являются точками нестабильности и стимулируют кристаллизацию жидкости – если переохладить газированную жидкость (в стакане, без крышки), а потом встряхнуть, то кристаллообразование произойдёт тоже лавинообразно.
Эти факты общеизвестны и не должны были вызвать удивления у доцента политеха. Возможно я не так понял ваш вопрос.
Как быстро утонет и наберёт воды изнутри, упавшая в воду машина? Какой самый лучший способ покинуть тонущую машину?
Позволю себе не согласиться с предыдущим мнением: во первых, разница в давлении не даст вам открыть дверь, следовательно его нужно выравнять пресловутым открыванием окон, что бы вода заполнила салон и как можно быстрее, здесь вытекает, во вторых, мы не знаем глубину водоема и значит нужно очень быстро выбираться , потому что кислорода просто может не хватить для всплытия, панику однозначно нужно пресечь и быстро и чётко объяснить последовательность своих и их действий пассажирам… Идеально да, если водоём неглубокий дождаться, когда машина опустится на дно, всех успокоить, медленно наполнить машину водой и выплыть
Прочитать ещё 5 ответов
Источник
Закономерности истечения вязкой несжимаемой жидкости через отверстия в стенках сосудов имеют важное приложение к задачам практики в нефтяной промышленности. Это, прежде всего, задачи о времени опорожнения всевозможных резеруаров и подвиженых емкостей.
Покажем, как, например, вычислить время истечения жидкости из резервуара, форма которого известна. Рассмотрим случай, когда жидкость вытекает в атмосферу через отверстие площадью в дне сосуда. Давление на свободной поверхности принимается равным атмосферному (рис. 10.9).
Рис. 10.9. Расчет времени опорожнения резервуара
Движение жидкости в рассматриваемом случае является неустановившимся, т. к. напор изменяется с течением времени, а, следовательно, меняется и расход вытекающей жидкости. В тех случаях, когда истечение жидкости происходит медленно, можно пользоваться гипотезой последовательной смены стационарных состояний.
Смысл этой гипотезы состоит в том, что если уровень жидкости в сосуде меняется медленно, то истечение жидкости в течение каждого интервала времени можно считать установившимся и пользоваться формулой, полученной для расхода жидкости при постоянном напоре
полагая в ней величину равной значению напора в данный момент времени. Таким образом:
. (10.22)
За малый интервал времени уровень жидкости в сосуде уменьшится на величину . Если площадь свободной поверхности жидкости в сосуде обозначить через , то объем жидкости, соответствующий уменьшению уровня жидкости на величину , дается выражением
, (10.23)
причем знак минус в этой формуле берется потому, что при .
Объем жидкости, вытекающей из сосуда, можно выразить по-другому, через расход :
.
Подставляя вместо его выражение, согласно, (10.22), получаем
. (10.24)
Сравнивая (10.23) и (10.24), находим:
,
или
. (10.25)
Для определения времени опорожнения резервуара от уровня до уровня проинтегрируем обе части уравнения (10.25): левую часть по от 0 до и правую часть по H от до . Получим:
(10.26)
Коэффициент , входящий в эту формулу, зависит, вообще говоря, от числа Рейнольдса , которое определяется переменной во времени величиной напора . Поэтому в общем случае интеграл в формуле (10.20) следует вычислять с учетом зависимости . Однако для многих, не слишком вязких жидкостей, величина коэффициента расхода остается постоянной на протяжении всего времени истечения. Рассмотрим случай, когда коэффициент расхода постоянен, тогда:
(10.27)
Если резервуар имеет постоянную площадь сечения (например, призматический резервуар, рис.10.10), то из (10.27) получим:
.
В частности, время полного опорожнения призматического резервуара от уровня до уровня определится по формуле:
(10.28)
В формуле (10.28) в числителе стоит удвоенный объем резервуара, а в знаменателе — расход жидкости из отверстия при постоянном напоре , поэтому
Таким образом, если умножить расход при постоянном напоре на время истечения, то получим удвоенный объем резервуара. Следовательно, для истечения количества жидкости, равного объему резервуара, при переменном уровне требуется время в два раза больше того, за которое вытекает то же количество жидкости при постоянном напоре, равном начальной высоте уровня жидкости в резервуаре.
Пример.Задача об определении времени истечения жидкости из цистерны. Требуется найти время опорожнения круглой горизонтальной цистерны с длиной и радиусом , рис. (10.10) и рис. (10.11).
| Рис. 10.10. Призматический резервуар | Рис. 10.11. Цилиндрическая цистерна |
Площадь опускающейся свободной поверхности жидкости в цистерне записывается в виде
где ,
тогда
(10.29)
Определим время полного опорожнения цистерны, при котором уровень жидкости будет уменьшаться от до . Из общей формулы (10.26) с учетом выражения (10.29) для получим:
. .(10.30)
Источник
Рассмотрим сосуд (рис. 1), площадь горизонтального сечения, которого является произвольной функцией расстояния сечения от дна сосуда.
Пусть высота уровня жидкости в сосуде в начальный момент времени t=0 равна h метров. Пусть, далее, площадь сечения на высоте х равна S(x), а площадь отверстия на дне сосуда есть S.
Известно, что скорость истечения жидкости U в тот момент, когда высота ее уровня равна x, определяется равенством U=k, где g=9,8 м/с2, k – коэффициент скорости истечения жидкости из отверстия. На бесконечно малом промежутке времени dt истечение жидкости можно считать равномерным, а потому за время dt вытечет столбик жидкости, высота которого Udt и площадь сечения S, что в свою очередь вызовет понижение уровня жидкости в сосуде на – dх.
В результате этих рассуждений приходим к дифференциальному уравнению
ksdt = – S(x) dx; (5)
которое можно переписать в виде
dt=-dx; (6)
Решим теперь следующую задачу. Цилиндрический резервуар с вертикальной осью высотой 6 м и диаметром 4 м имеет на дне круглое отверстие радиусом 1/12 м. Требуется установить зависимость уровня воды в резервуаре от времени t, а также определить время, в течение которого вытечет вся вода.
По условиям задачи S(x)=4р; S=1/144. Так как для воды k=0,6, то уравнение (6) примет вид dt = -dx;
Интегрируя это дифференциальное уравнение, приходим к соотношению t= 434,304 ;которое и дает искомую зависимость уровня воды от времени t. Если теперь в последнем равенстве положить х=6, то получим, что вся вода вытечет из резервуара приблизительно через 18 минут.
Вторая задача состоит в следующем. Известно, что древние водяные часы представляли собой чашу (рис. 2), из которой через небольшое отверстие на дне вытекала вода. Такие часы использовались в греческих и римских судах для хронометрирования речей адвокатов, чтобы не допускать слишком долгих выступлений. Требуется найти форму водяных часов, при которой уровень воды убывал бы в чаше с постоянной скоростью.
Задача легко решается с помощью выведенного выше уравнения (6), которое мы только перепишем в виде
=-; (7)
Именно, учитывая, что чашу можно рассматривать как поверхность вращения, в соответствии с обозначениями на (рис. 2) из уравнения (7) получаем, что
(8)
Где a=Ux=- проекция свободной поверхности жидкости на ось x, которая по условию задачи есть величина постоянная. Возведя обе части уравнения (8) в квадрат приходим к уравнению
x=cr4; (9)
где c=a2р2/(2gk2s2). Последнее означает, что форма поверхности водяных часов получается вращением кривой (9) вокруг оси х.
Приведем один из примеров использования дифференциальных уравнений для выбора правильной стратегии при решении задач поиска.
Пусть, например, миноносец охотится за подводной лодкой в густом тумане. В какой-то момент времени туман поднимается и подводная лодка оказывается обнаруженной на поверхности воды на расстоянии 3 миль от миноносца. Скорость миноносца вдвое больше скорости подводной лодки. Требуется определить траекторию (кривую погони), по которой должен следовать миноносец, чтобы он прошел точно над подводной лодкой, если последняя сразу же погрузилась после ее обнаружения и ушла на полной скорости прямым курсом в неизвестном направлении.
Для решения сформулированной задачи введем полярные координаты r, O таким образом, чтобы полюс О находился в точке обнаружения подводной лодки, а полярная ось r проходила через точку, в которой в момент обнаружения подводной лодки был миноносец (рис. 3). Дальнейшие рассуждения основаны на следующих соображениях. Прежде всего, миноносцу надо занять такую позицию, чтобы он и подводная лодка находились на одном расстоянии от полюса О. Затем миноносец должен двигаться вокруг полюса О по такой траектории, чтобы оба движущихся объекта все время находились на одинаковом расстоянии от точки О. Только в этом случае миноносец, обходя вокруг полюса О, пройдет над подводной лодкой. Из вышесказанного следует, что сначала миноносец должен идти прямым курсом к точке О до тех пор, пока он не окажется на том же расстоянии х от полюса О, что и подводная лодка.
Очевидно, что расстояние х можно найти либо из уравнения
,
либо из уравнения
,
где u – скорость подводной лодки, а 2u – скорость миноносца. Решая последние уравнения, находим, что либо расстояние х равно одной, либо трем милям.
Теперь, если «встречи» не произошло, то миноносец должен в дальнейшем двигаться вокруг полюса О (по направлению движения часовой стрелки или против), удаляясь от последнего со скоростью подводной лодки u. Разложим скорость миноносца 2u на две составляющие: радиальную urи тангенциальную ut (рис. 3).
Радиальная составляющая – это скорость, с которой миноносец удаляется от полюса О, т.е.
ur=.
Тангенциальная составляющая – это линейная скорость вращения миноносца относительно полюса. Она, как известно, равна произведению угловой скорости на радиус r, т.е.
ur=r.
Но так как ur = u, то
ur==u.
Итак решение исходной задачи сводится к решению системы двух дифференциальных уравнений
, r= u,
Которая, в свою очередь, может быть сведена к одному уравнению
исключением переменной t.
Решая последнее дифференциальное уравнение, получаем, что
r=C,
где С – произвольная постоянная.
Учитывая теперь, что миноносец начинает движение вокруг полюса О с полярной оси r на расстоянии х миль от точки О, т.е. учитывая, что r=1 при O=0 и r=3 при O=-р я, приходим к выводу, что в первом случае C=1, а во втором С = З. Таким образом, чтобы выполнить свою задачу, миноносец должен пройти две или шесть миль прямым курсом по направлению к месту обнаружения подводной лодки, а затем двигаться либо по спирали r= либо по спирали r=3.
Источник