Наливай воду в два сосуда разной ширины и заполняй таблицы
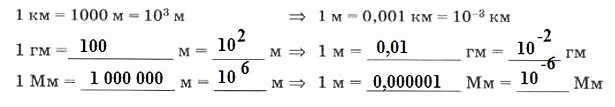
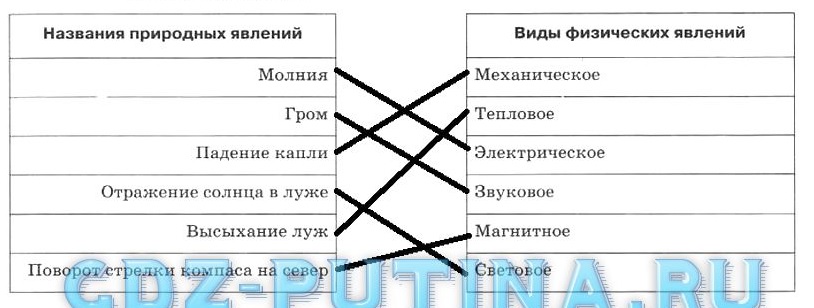
1.1. Соедините линиями названия природных явлений и соответствующие им виды физических явлений.
1.2. Отметьте галочкой свойства, которыми обладают и камень, и резиновый жгут.
✓ Хрупкость при низкой температуре.
1.3. Заполните пропуски в тексте так, чтобы получились названия наук, изучающих различные явления на стыке физики и астрономии, биологии, геологии.
Движение крови по сосудам организма изучает
био
физика.
Распространение взрывной волны в толще Земли изучает
гео
физика.
Причину свечения звезд, изменения во Вселенной изучает
астро
физика.
1.4. Запишите в стандартном виде следующие числа по приведенному выше образцу.
2.1. Обведите в рамочку те свойства, которыми физическое тело может не обладать.
2.2. На рисунке изображены тела, состоящие из одного и того же вещества. Запишите название этого вещества.

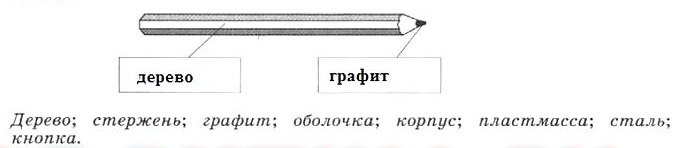
2.3. Выберите из предложенных слов два слова, обозначающие вещества, из которых сделаны соответствующие части простого карандаша, и запишите их в пустые окошки.
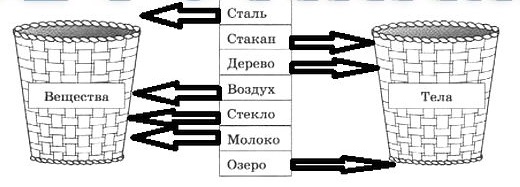
2.4. С помощью стрелочек «рассортируйте» слова по корзинам в соответствии с их названиями, отражающими разные физические понятия.

2.5. Запишите числа по приведенному образцу.
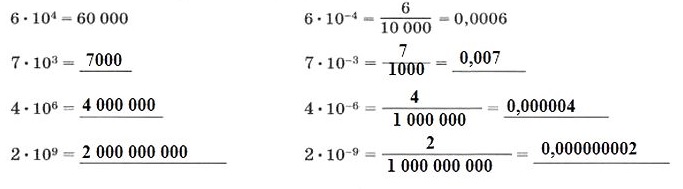
3.1. На уроке физики учитель поставил ученикам на столы одинаковые на вид магнитные стрелки, размещенные на остриях игл. Все стрелки повернулись вокруг своей оси и замерли, но при этом одни из них оказались повернутыми на север синим концом, а другие – красным. Ученики удивились, но в ходе беседы некоторые из них высказали свои гипотезы, почему так могло произойти. Отметьте, какую выдвинутую учениками гипотезу можно опровергнуть, а какую – нет, зачеркнув ненужное слово в правой колонке таблицы.

3.2. Выберите правильное продолжение фразы « В физике явление считается реально протекающим, если…»
✓ его наблюдали несколько ученых
3.3. Допишите предложение.
Наблюдения природных явлений отличаются от опытов тем, что опыты – это эксперименты, при которых человек создает и поддерживает определенные условия. Наблюдения природных явлений не подразумевают человеческого вмешательства.
3.4. Выберите правильное продолжение фразы.
21 июля 1969 г. впервые была осуществлена посадка на Луну американского космического корабля с астронавтами на борту. Это событие является…
✓ экспериментом
3.5. Еще в древности люди наблюдали, что:

4.1. Закончите фразу.
Физическая величина – это характеристика тела или явления, которую можно измерить и сравнить.
4.2. Вставьте в текст недостающие слова и буквы.
В Международной системе единиц (СИ):

4.3. а) Выразите кратные единицы длины в метрах и наоборот.
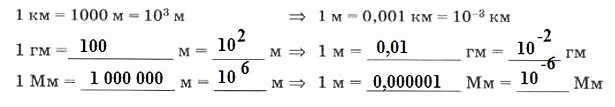
б) Выразите метр в дольных единицах и наоборот.
в) Выразите секунду в дольных единицах и наоборот.
г) Выразите в основных единицах СИ значения длины.

д) Выразите в основных единицах СИ значения интервалов времени.
е) Выразите в основных единицах СИ значения следующих величин.

4.4. Измерьте линейкой ширину l страницы учебника. Выразите результат в сантиметрах, миллиметрах и метрах.
l =
16,7
см =
167
мм =
0,167
м
4.5. На стержень намотали провод так, как показано на рисунке. Ширина намотки оказалась равной l=9 мм. Каков диаметр d провода? Ответ выразите в указанных единицах.
4.6. Запишите значения длины и площади в указанных единицах по приведенному образцу.

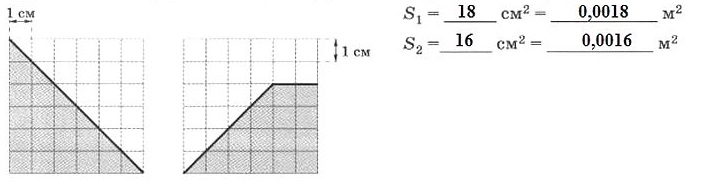
4.7. Определите площадь треугольника S1 и трапеции S2 в указанных единицах.
4.8. Запишите значения объема в основных единицах СИ по приведенному образцу.
4.9. В ванну налили сначала горячей воды объемом 0,2 м3, затем добавили холодной воды объемом 2 л. Каков объем воды в ванне?
0,2 м3 + 2 л = 0,2 м3 + 0,002 м3 = 0,202 м3
4.10. Допишите предложение. «Цена деления шкалы термометра составляет _____».

5.1. Воспользуйтесь рисунком и заполните пропуски в тексте.

[/center]
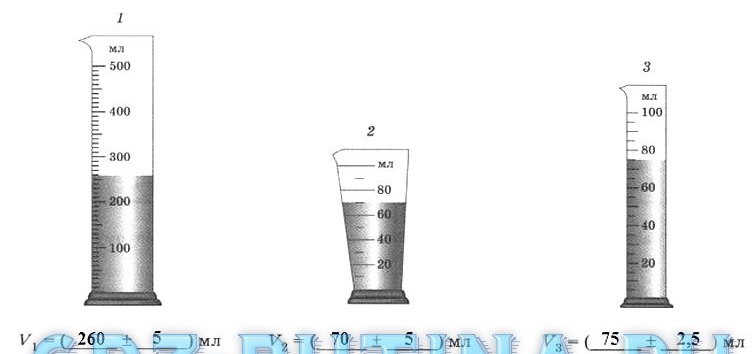
5.2. Запишите значения объема воды в сосудах с учетом погрешности измерения.
[center]
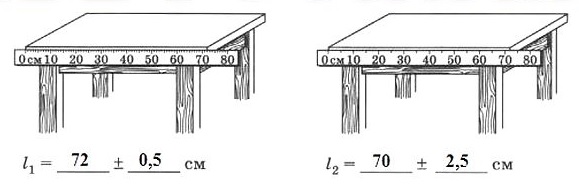
5.3. Запишите значения длины стола, измеренной разными линейками, с учетом погрешности измерений.
5.4. Запишите показания часов, изображенных на рисунке.

5.5. Ученики измерили длину своих столов разными приборами и результаты записали в таблицу.

6.1. Подчеркните названия устройств, в которых используется электродвигатель.
Утюг,
лифт
, телевизор,
кофемолка
,
мобильный телефон
, калькулятор.
6.2. Домашний эксперимент.
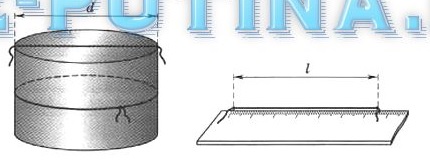
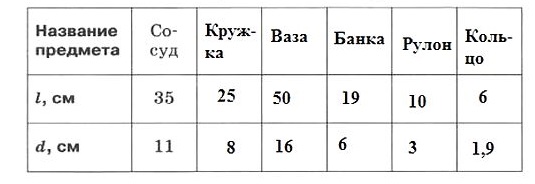
1. Измерьте диаметр d и длину окружности l у пяти предметов цилиндрической формы с помощью нити и линейки (см. рис.). Названия предметов и результаты измерений запишите в таблицу. Используйте предметы разного размера. Для примера в первой колонке таблицы уже поставлены значения, полученные для сосуда диаметром d = 11 см и длиной окружности l = 35 см.
2. Используя таблицу, постройте график зависимости длины окружности l предмета от его диаметра d . Для этого на координатной плоскости нужно построить шесть точек согласно данным таблицы и соединить их прямой линией. Для примера на плоскости уже построена точка с координатами (d, l ) для сосуда. Аналогично на этой же плоскости постройте точки для других тел.
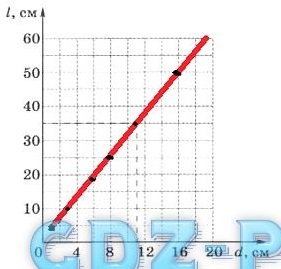
3. Используя полученный график, определите, чему равен диаметр d цилиндрической части пластиковой бутылки, если длина ее окружности l = 19см.
d = 60 см
6.3. Домашний эксперимент.
1. Измерьте размеры спичечного коробка с помощью линейки с миллиметровыми делениями и запишите эти значения с учетом погрешности измерения.
Длина коробка a = ( 50
±
0,5
) мм.
Ширина коробка b = (
32
±
0,5
) мм.
Высота коробка c = (
12
±
0,5
) мм.
Предыдущая запись означает, что истинные значения длины, ширины и высоты коробка лежат в пределах:
a: от
49,5
до
50,5
мм;
b: от
31,5
до
32,5
мм;
с: от
11,5
до
12,5
мм.
2. Рассчитайте, в каких пределах лежит истинное значение объема коробка.
от (49,5*31,5*11,5) мм3 до (50,5*32,5*12,5) мм3
Объем коробка лежит в пределах от
17931,4 мм3
до
20515,6 мм3
.
Источник
18.1. Вставьте в текст пропущенные слова. «Говорят, что скорость тела изменилась, если изменился _____ скорости или ______».

18.2. Домашний эксперимент.
Положите на стол лист бумаги, а сверху поставьте пластиковую бутылку с водой, закрытую крышкой. Быстро выдерните лист из-под бутылки. Опишите свои наблюдения. Объясните наблюдаемое явление.
Бутылка остается на месте, так как масса бутылки велика
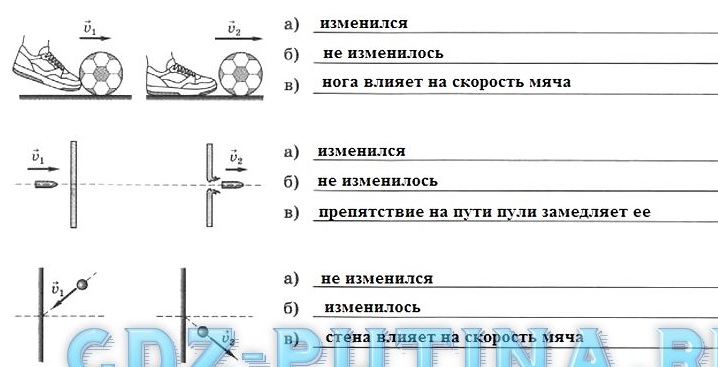
18.3. Ответьте на вопросы для каждого случая, показанного на рисунке.
а) Изменился ли модуль скорости тела?
б) Изменилось ли направление скорости тела?
в) Действие какого из тел послужило причиной изменения скорости другого тела?
18.4. При повороте автобуса туловища сидящих в автобусе пассажиров отклоняются от вертикального положения. Объясните явление.

Автобус вместе с пассажирами едет на некоторой скорости, а когда автобус поворачивает, то пассажиры продолжают с той же скоростью по инерции двигаться дальше, из-за этого туловища отклоняются от своего положения.
18.5. Выберите правильное утверждение.
В вагоне поезда, движущегося с постоянной скоростью, друг против друга сидят мальчики. Один мальчик другому бросает конфету, прицеливаясь ему прямо в руки. Конфета попадет … .
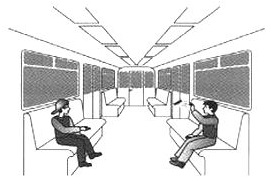
✓ прямо в руки второму мальчику
19.1. Заполните пропуски в тексте, используя слова: лодка; меняется; двигаться; скорость; взаимодействуют; друг на друга; действие.

19.2. Выберите правильное утверждение.
Известно, что магнит притягивает к себе железные предметы. Если в ванночке на поверхности воды недалеко друг от друга расположить магнит и железный болт примерно таких же размеров на пенопластовых пластинах и оставить их в покое, то через некоторое время … .
✓ и магнит, и болт начнут перемещаться относительно ванночки навстречу друг друга
19.3. Заполните пропуски в тексте, используя слова: воздух; земля; вода.

19.4. Выберите правильное утверждение.
Два друга – Иван и Петр стоят на роликовых коньках. Иван держится за один конец веревки, а Петр тянет за другой ее конец, стараясь подтянуть к себе Ивана. При этом … .
✓ оба мальчика движутся относительно земли навстречу друг другу
20.1. Заполните пропуски в тексте. «Масса тела – это физическая величина, характеризующая его ____».

20.2. С помощью линий установите соответствие между понятиями, расположенными справа и слева.
20.3. Выберите правильное утверждение.
Папа и сын, стоя на коньках, оттолкнулись друг от друга. После толчка скорость сына оказалась … .
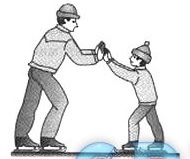
✓ больше скорости папы
20.4. Выберите правильный ответ.
Мальчик, находясь в неподвижной лодке, бросил камень массой 5 кг в сторону кормы лодки со скоростью 2 м/с. Какова была скорость лодки относительно воды сразу после броска, если масса лодки с мальчиком равна 100 кг?
20.5. Запишите значения массы тел в указанных единицах по приведенному образцу.
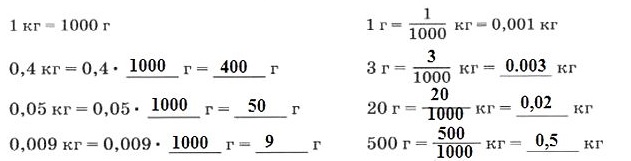
20.6. Запишите значения массы тел в указанных единицах по приведенному образцу.
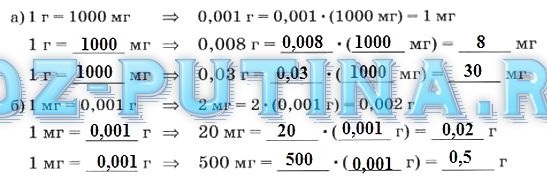
21.1. Для уравновешивания тела на рычажных весах были использованы наборы гирь, масса которых указана в таблице. Чему равна масса каждого тела?

21.2. Две одинаковые тележки, между которыми зажата пружина, соединены нитью. На левую тележку насыпают песок, на правую – ставят гирю. После пережигания нити пружина распрямляется, расталкивая тележки в противоположные стороны, в результате чего они приобретают одинаковые скорости. Чему равна масса песка на левой тележке? Ответ поясните.
21.3. На две тележки, массой по 2 кг каждая, поместили песок и гирю (см. рис.). После пережигания нитки тележки разъезжаются в противоположные стороны. При этом скорость левой тележки в 2 раза меньше, чем скорость правой. Чему равна масса песка на левой тележке? Ответ поясните.

21.4. Домашний эксперимент.
Определите массу своего тела с помощью напольных весов.

1. Зарисуйте шкалу прибора.
2. Определите цену деления шкалы прибора. 1 кг
3. Запишите результат измерения с учетом погрешности измерения.
m = (45 ± 0,5) кг.
22.1. Заполните пропуски в тексте. «Плотность вещества показывает, какова масса единицы объема вещества, и высчитывается по формуле ______».

22.2. Заполните таблицу по приведенному образцу.
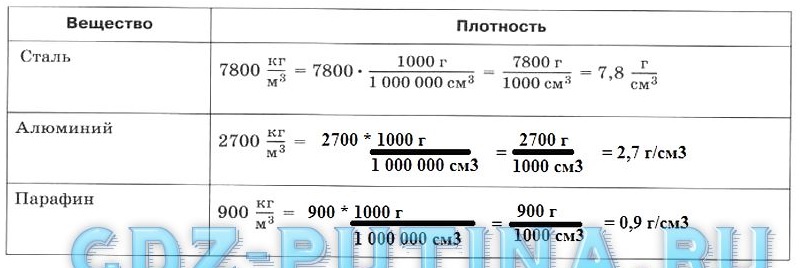
22.3. Пользуясь таблицей1 плотностей веществ, вставьте в текст пропущенные слова.

22.4. Заполните пропуски в тексте.

Два кубика А и В из разных веществ уравновешены на весах. Из вещества с большей плотностью изготовлено тело А, так как его размеры меньше, чем у тела В.
22.5. Вставьте в текст пропущенное слово.
На чаши весов кладут стеклянный и мраморный кубики одинакового размера. Перетянет чаша с кубиком
из мрамора.
22.6. Бутылка без масла имеет массу 50 г, а с маслом – 450 г. Какова по этим данным плотность масла, если объем бутылки 0,5 л?

23.1. Чему равна масса тела объемом 3 м3 и плотностью 4000 кг/м3?

23.2. Впишите в предложение недостающее слово: больше или меньше. Запишите формулу, на основе которой вы сделали выбор.

23.3. Какова масса керосина, налитого в измерительный цилиндр?

23.4. Два одинаковых измерительных цилиндра с различными жидкостями уравновешены на рычажных весах. Определите плотность жидкости, находящейся в цилиндре 2. Ответ округлите до сотен. По таблице плотности определите, какая это жидкость.
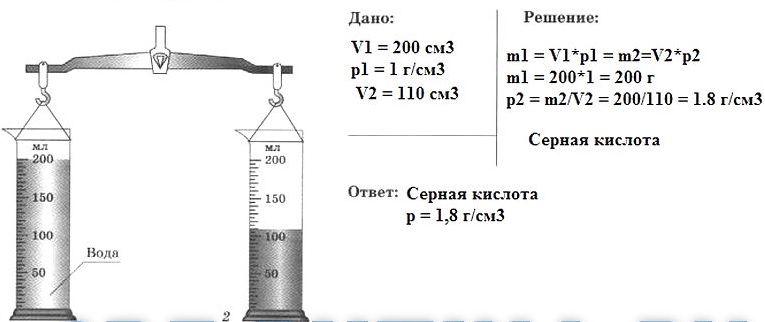
23.5. В измерительный цилиндр с водой опустили гирьку массой 100 г. Рассчитайте плотность вещества, из которого изготовлена гирька. Ответ округлите до сотен. По таблице плотности определите, какое это может быть вещество.

23.6. Алюминиевый шарик массой m = 100 г опущен в сосуд с водой. Есть ли в шарике полость?

23.7. Выберите правильный ответ.
Два кубика одинакового размера, изготовленные из стали и имеющие внутри себя полости, кладут на разные чаши весов. В результате взвешивания … .
✓ перевесит кубик, обладающий полостью меньшего размера
Источник
Рабочая тетрадь по физике 7 класс Т.А. Ханнанова (к учебнику А.В. Перышкина)
18.1. Вставьте в текст пропущенные слова. «Говорят, что скорость тела изменилась, если изменился _____ скорости или ______».
18.2. Домашний эксперимент.
Положите на стол лист бумаги, а сверху поставьте пластиковую бутылку с водой, закрытую крышкой. Быстро выдерните лист из-под бутылки. Опишите свои наблюдения. Объясните наблюдаемое явление.
18.3. Ответьте на вопросы для каждого случая, показанного на рисунке.
а) Изменился ли модуль скорости тела?
б) Изменилось ли направление скорости тела?
в) Действие какого из тел послужило причиной изменения скорости другого тела?
18.4. При повороте автобуса туловища сидящих в автобусе пассажиров отклоняются от вертикального положения. Объясните явление.
18.5. Выберите правильное утверждение.
В вагоне поезда, движущегося с постоянной скоростью, друг против друга сидят мальчики. Один мальчик другому бросает конфету, прицеливаясь ему прямо в руки. Конфета попадет … .
19.1. Заполните пропуски в тексте, используя слова: лодка; меняется; двигаться; скорость; взаимодействуют; друг на друга; действие.
19.2. Выберите правильное утверждение.
Известно, что магнит притягивает к себе железные предметы. Если в ванночке на поверхности воды недалеко друг от друга расположить магнит и железный болт примерно таких же размеров на пенопластовых пластинах и оставить их в покое, то через некоторое время … .
19.3. Заполните пропуски в тексте, используя слова: воздух; земля; вода.
19.4. Выберите правильное утверждение.
Два друга – Иван и Петр стоят на роликовых коньках. Иван держится за один конец веревки, а Петр тянет за другой ее конец, стараясь подтянуть к себе Ивана. При этом … .
20.1. Заполните пропуски в тексте. «Масса тела – это физическая величина, характеризующая его ____».
20.2. С помощью линий установите соответствие между понятиями, расположенными справа и слева.
20.3. Выберите правильное утверждение.
Папа и сын, стоя на коньках, оттолкнулись друг от друга. После толчка скорость сына оказалась … .
20.4. Выберите правильный ответ.
Мальчик, находясь в неподвижной лодке, бросил камень массой 5 кг в сторону кормы лодки со скоростью 2 м/с. Какова была скорость лодки относительно воды сразу после броска, если масса лодки с мальчиком равна 100 кг?
20.5. Запишите значения массы тел в указанных единицах по приведенному образцу.
20.6. Запишите значения массы тел в указанных единицах по приведенному образцу.
21.1. Для уравновешивания тела на рычажных весах были использованы наборы гирь, масса которых указана в таблице. Чему равна масса каждого тела?
21.2. Две одинаковые тележки, между которыми зажата пружина, соединены нитью. На левую тележку насыпают песок, на правую – ставят гирю. После пережигания нити пружина распрямляется, расталкивая тележки в противоположные стороны, в результате чего они приобретают одинаковые скорости. Чему равна масса песка на левой тележке? Ответ поясните.
21.3. На две тележки, массой по 2 кг каждая, поместили песок и гирю (см. рис.). После пережигания нитки тележки разъезжаются в противоположные стороны. При этом скорость левой тележки в 2 раза меньше, чем скорость правой. Чему равна масса песка на левой тележке? Ответ поясните.
21.4. Домашний эксперимент.
Определите массу своего тела с помощью напольных весов.
1. Зарисуйте шкалу прибора.
2. Определите цену деления шкалы прибора.
3. Запишите результат измерения с учетом погрешности измерения.
22.1. Заполните пропуски в тексте. «Плотность вещества показывает, какова масса единицы объема вещества, и высчитывается по формуле ______».
22.2. Заполните таблицу по приведенному образцу.
22.3. Пользуясь таблицей1 плотностей веществ, вставьте в текст пропущенные слова.
22.4. Заполните пропуски в тексте.
Два кубика А и В из разных веществ уравновешены на весах. Из вещества с большей плотностью изготовлено тело А, так как его размеры меньше, чем у тела В.
22.5. Вставьте в текст пропущенное слово.
22.6. Бутылка без масла имеет массу 50 г, а с маслом – 450 г. Какова по этим данным плотность масла, если объем бутылки 0,5 л?
23.1. Чему равна масса тела объемом 3 м3 и плотностью 4000 кг/м3?
23.2. Впишите в предложение недостающее слово: больше или меньше. Запишите формулу, на основе которой вы сделали выбор.
23.3. Какова масса керосина, налитого в измерительный цилиндр?
23.4. Два одинаковых измерительных цилиндра с различными жидкостями уравновешены на рычажных весах. Определите плотность жидкости, находящейся в цилиндре 2. Ответ округлите до сотен. По таблице плотности определите, какая это жидкость.
23.5. В измерительный цилиндр с водой опустили гирьку массой 100 г. Рассчитайте плотность вещества, из которого изготовлена гирька. Ответ округлите до сотен. По таблице плотности определите, какое это может быть вещество.
23.6. Алюминиевый шарик массой m = 100 г опущен в сосуд с водой. Есть ли в шарике полость?
23.7. Выберите правильный ответ.
Два кубика одинакового размера, изготовленные из стали и имеющие внутри себя полости, кладут на разные чаши весов. В результате взвешивания … .
Источник
Задачи на переливание.
Термин «литр» введен в честь француза Клода-Эмиля-Жана-Батиста Литра. Он жил в XVIIIвеке и занимался производством винных бутылок. Считается, что Литр – первый из тех. Кто стал производить лабораторную посуду. В частности, он придумал градуированные стеклянные цилиндры. Известно, что его родители так же занимались производством винных бутылок. В 1763 году на 47-м году жизни Литр предложил измерять объемы жидкости с помощью единицы, которую в последствии назвали литром.
1. Как пользуясь банками в 3л и 5л, набрать воды ровно 1л?
2. Как отметить 4л воды с помощью сосудов в 3л и 5 л?
3. Как, имя лишь два сосуда емкостью 5л и 7 л, отметить6л воды?
4. Каким образом из реки можно принести ровно 6л воды, если имеется только два ведра: одно – емкостью 4л. другое – 9л?
5. Бидон емкостью 10л заполнен молоком. Требуется перелить из этого бидона 5л в семилитровый бидон, используя при этом еще один бидон, вмещающий 3л.
6. Имея два бидона емкостью 4л и 5л, можно ли налить в ведро 3л воды. Если емкость ведра не менее 3л?
7. (задача Пуассона) Известному французскому математику Симону Пуассону(1981-1840) в юности предложили задачу. Заинтересовавшись ею, Пуассон затем увлекся математикой и посвятил этой науке всю свою жизнь. Вот эта задача. Некто имеет 12 пинт вина и хочет отлить из этого количества половину, но у него нет сосуда в 6 пинт. Зато есть два других сосуда: в 8 пинт и 5 пинт. Спрашивается: каким образом налить 6 пинт в сосуд на 8 пинт?
Все задачи на переливания принципиально делятся на 2 типа.
Первый – когда у нас есть много жидкости (озеро, бесконечно большая бочка, водопровод), и мы можем наполнять доверху сосуды сколь угодно большое количество раз, то есть количество жидкости не ограничено. При этом мы можем безбоязненно выливать воду из сосудов.
Второй – это когда жидкости у нас ровно столько, сколько изначально налито в сосудах (в этом случае у нас обычно не простая жидкость, а какая-либо особенная: молоко, сок и т. д.). Чаще всего эту жидкость ещё и нельзя проливать – авторы стараются это отдельно оговаривать. Если же мы можем выливать жидкость, то в условиях задачи обычно присутствует какой-либо персонаж, который может пить данный тип жидкости: Кот Баюн, сосед Гриша и т. п.
Также стоит понять принцип задач на переливания: например, если у нас есть сосуд объемом 8 литров и 5 литров, и нам надо отмерить 2 литра воды, мы не имеем права на следующее решение: «Наполним восьмилитровый сосуд на четверть – таким образом, мы и получим 2 литра воды». Или: «Давайте опустошим наш 5 литровый сосуд на 60%, тогда в нем останется ровно 2 литра воды». Нет, так делать нельзя. (Если у ребёнка в этом месте возникают вопросы, то вы можете придумать, например, такое оригинальное объяснение: «А вдруг наш сосуд – это какая-нибудь замысловатая ваза (или древняя амфора), конечно, без шкалы делений!» Или даже просто банка не вполне симметрична, а на глаз определить середину – проблематично…) Мы можем либо полностью наполнять сосуды, либо полностью опустошать их, либо переливать из одного сосуда в другой. При этом мы можем пользоваться тем, что при этих операциях часть воды может оставаться в сосуде, из которого дополняется другой сосуд.
Для примера решим три задачи.
Задача 1-го типа
Для приготовления компота маме нужно налить в 5-литровую кастрюли 4 литра воды. Как маме справиться с этой задачей, если у мамы есть кроме этой кастрюли ещё 3-литровая банка, водопроводный кран и раковина, куда можно выливать воду?
Решение.
Нальём в 3-литровую банку воду и перельём её в кастрюлю. Затем еще раз наполним банку и выльём в кастрюлю, сколько поместится. Тогда в кастрюле будет 5 литров и 1 литр в 3-литровой банке. Теперь выльем всю воду из кастрюли в раковину. Затем перельем литр из банки в кастрюлю и добавим ещё три литра, наполнив банку ещё раз. Теперь в кастрюле 1 + 3 = 4 литра, что и требовалось. Задача решена.
Наше решение можно проиллюстрировать таблицей:

Итак, мы получили желанные 4 литра. Задача решена! Мы считаем, что такой способ решения с помощью таблицы является достаточно наглядным, и рекомендуем для вашего совместного с ребёнком решения.
Задача 2-го типа
У Марьи есть 2 кувшина объёмом 8 и 3 литра. В восьмилитровом кувшине налит весь имеющийся у Марьи кисель. Как отмерить 2 литра киселя? Все излишки киселя можно отдать Коту Баюну, который просто обожает это лакомство.
Решение.
Наполним трехлитровый кувшин доверху из восьмилитрового, после этого у нас будет 5 литров в 8-литровом и 3 литра в 3-литровом. Отдадим весь кисель из 3-литрового кувшина Коту Баюну. После этого у нас осталось 5 литров в 8-литровом и 3-литровый кувшин пуст. Снова наполним 3-литровый кувшин из 8-литрового. После этой операции в 8-литровом кувшине у нас останется ровно 2 литра (5 – 3 = 2). Мы отмерили 2 литра. Задача решена!
Решение также можно проиллюстрировать таблицей:

Ещё одна задача 2-го типа
Задача 3.
В кастрюле налито 8 литров супа. Есть также пустые 3-х и 5-тилитровая банки. Требуется отмерить 4 литра супа. Как это сделать, если суп нельзя проливать?
Решение.
1 способ. Нальём суп доверху в меньшую банку, затем перельём полученные три литра в 5-литровую банку, а 3-литровую наполним снова. Теперь будем лить суп из 3-литровой банки в 5-литровую, пока она не наполнится доверху. Тогда в меньшей банке останется 1 литр (5 – 3 = 2 и 3 – 2 = 1). Перельём 5 литров в кастрюлю, а 1 литр – в большую банку. Затем перельём 3 литра из кастрюли в меньшую банку. После этого в кастрюле останется ровно 4 литра. Задача решена.
2 способ. Нальём суп доверху в большую банку, тогда в кастрюле останется ровно 3 литр. Перельём из большой банки в меньшую 3 литра, после чего перельём их в кастрюлю. Перельём 2 литра из большой банки в меньшую, и наполним большую банку доверху супом из кастрюли. После чего дольём меньшую банку (там было 2 литра, а помещается 3) из большей банки. Получим 4 литра в большой банке. Задача решена.
Проиллюстрируем оба способа таблицам:

Советуем использовать таблицу при решении подобных задач.
Также ребёнку можно дать следующую подсказку. Речь пойдет о задачах, где разрешается выливать жидкости. Пусть в какой-то момент наполнены все сосуды, может быть, частично. Тогда перед ребенком стоит вопрос о том, откуда вылить жидкость. Выливать стоит из полного сосуда, а не из полупустого, так как количество литров в полном сосуде мы всегда с лёгкостью снова получим, тогда как получить полупустой сосуд − дело затруднительное. Надеемся, что в процессе работы вы сами сможете придумать множество оригинальных приемов и способов!
Обратите внимание, что приведённые решения могут не являться единственными. Ни в коем случае не говорите ребёнку, что он как-то не так стал решать задачу, если первым ходом он, допустим, налил воду из крана не в больший, а в меньший сосуд! Просто тщательно следите за его действиями. В большинстве задач есть как минимум 2 способа решения, и, скорее всего, при правильном выполнении переливаний ваш ребёнок в конечном итоге получит результат. Правда, возможно, за большее число ходов, зато – сколько удовольствия от самостоятельного решения без подсказок он получит!
Задачи на переливание — один из видов старинных задач. Они возникли много веков назад, но до сих пор вызывают интерес у любителей математики и их часто можно встретить в олимпиадных заданиях для 5–6-х классов. Однако данный вид логических задач целесообразно рассматривать и с учащимися среднего звена (7-8 классы).
Суть этих задач сводится к следующему: имея несколько сосудов разного объема, один из которых наполнен жидкостью, требуется разделить ее в каком-либо отношении или отлить какую-либо ее часть при помощи других сосудов за наименьшее число переливаний.
В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи. Если не сказано ничего другого, считается, что
– все сосуды без делений,
– нельзя переливать жидкости “на глаз”
– невозможно ниоткуда добавлять жидкости и никуда сливать.
Мы можем точно сказать, сколько жидкости в сосуде, только в следующих случаях:
знаем, что сосуд пуст,
знаем, что сосуд полон, а в задаче дана его вместимость,
в задаче дано, сколько жидкости в сосуде, а переливания с использованием этого сосуда не проводились
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, и после переливания вся жидкость поместилась в один из них
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, известна вместимость того сосуда, в который переливали, и известно, что вся жидкость в него не поместилась: мы можем найти, сколько ее осталось в другом сосуде.
Чаще всего используются словесный способ решения (т.е. описание последовательности действий) и способ решения с помощью таблиц, где в первом столбце (или строке) указываются объемы данных сосудов, а в каждом следующем — результат очередного переливания. Таким образом, количество столбцов (кроме первого) показывает количество необходимых переливаний.
Задача № 1. Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.
Задача № 2. Винни-Пух и пчелы.
Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.
Решение лучше и удобнее оформить в виде таблицы:
Задача № 3. Бэтмен и Человек-Паук.
Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу.
Ход рассуждений таков:
Как в результате получить 7 литров? – Нужно к 5 литрам долить 2 л. А где их взять? – Из 5-литрового сосуда отлить 3 л. А как их получить? В 8-литровый перелить из 5-литрового 5 литров, потом еще три.
Решение задачи показано в таблице:
Будем “шаги” переливаний записывать в виде строки из трех чисел.
При этом сосуды размещены слева направо по мере убывания их вместимости:
Решение:
В скобках – второй вариант решения.
Задача № 6. Молоко из Простоквашино.
Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?
Переливаем из 8-литрового ведра 5 литров молока в 5-литровое. Переливаем из 5-литрового бидона 3 литра в 3-литровый бидон.
Переливаем их теперь в 8-литровое ведро. Итак, теперь 3-литровое ведро пусто, в 8-литровом 6 литров молока, а в 5-литровом – 2 литра молока.
Переливаем 2 литра молока из 5-литрового бидона в 3-литровый, а потом наливаем 5 литров из 8-литрового ведра в 5-литровый бидон. Теперь в 8-литровом 1 литр молока, в 5-литровом – 5, а в 3-литровом – 2 литра молока.
Доливаем дополна 3-литровый бидон из 5-литрового и переливаем эти 3 литра в 8-литровое ведро. В 8-литровом ведре стало 4 литра, так же, как и в 5-литровом бидоне. Задача решена.
Решение: Задача № 8. Том Сойер.
Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
Задача № 9. Губка Боб.
Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда 5-литровый и 7-литровый. Как ему это сделать?
Решение задач на переливание векторным способом
Существенным недостатком табличного способа решения является отсутствие четкого алгоритма действий, невозможность предвидеть ближайшие шаги. Составлять такие таблицы можно довольно долго, так и не придя к нужному результату.
Механизировать решение этих задач с помощью «умного» шарика предложил Я.И. Перельман в книге «Занимательная геометрия». Для каждого случая предлагалось строить бильярдный стол особой конструкции, длины двух сторон которого численно равны объему двух меньших сосудов. Далее, из острого угла этого стола вдоль одной из сторон нужно «запустить» шарик, который по закону «угол падения равен углу отражения» будет сталкиваться с бортами стола, показывая тем самым последовательность переливаний. На бортах стола нанесена шкала, цена деления которой соответствует выбранной единице объема. В результате движения шарик либо ударяется о бортик в нужной точке (тогда задача имеет решение), либо не ударяется (тогда считается, что задача решения не имеет).
Предложим еще один способ решения задач на переливание — с помощью векторов.
