Напряжение в тонкостенном сосуде
С позиций конструктивного оформления сварных соединений и технологии изготовления сосуд считают тонкостенным, если толщина стенки не превышает 7-10 мм.
Тонкостенным сосудам обычно придают форму цилиндра, сферы или тора (рис. 10.12).
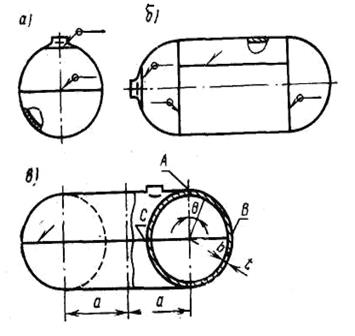
Рис.10.12. Характерные типы тонкостенных сосудов:
а – сферический; б – цилиндрический; в – торовый
Выбор формы может определяться различными соображениями. Сферический сосуд при заданной емкости имеет минимальную массу, который можно компактно разместить, например, вокруг камеры сгорания ЖРД, цилиндрическая форма сосуда обеспечивает наиболее технологичное конструктивное оформление. Соединения осуществляют продольными, кольцевыми и круговыми швами. Тонкостенные сосуды обычно являются конструктивными элементами различных транспортных установок. В тех случаях, когда не требуется экономия массы, используют хорошо сваривающиеся материалы невысокой прочности. В зависимости от свариваемости металла и его чувствительности к концентрации напряжений представления о технологичности одного и того же конструктивного оформления могут оказаться различными. Характерная для низкоуглеродистых сталей хорошая свариваемость и малая чувствительность к концентрации напряжений позволяют использовать любые типы сварных соединений. Поэтому при использовании таких материалов главной задачей ставится снижение трудоемкости изготовления изделия. Примером этого служат конструкции тормозных воздушных баллонов грузовых автомобилей, изготовляемых в условиях крупносерийного и массового производства, когда технологичность изделия особенно важна. Такой баллон (рис. 10.13 а) имеет обечайку из горячекатаной стали 20кп и два штампованных днища из стали 08кп толщиной 2,5 мм. К днищу дуговой или рельефной сваркой приварены бобышки. Соединение днища с обечайкой нахлесточное. Такое решение облегчает механизацию сборки путем одновременной запрессовки обоих днищ в обечайку. Для этого отбортованной части днищ придают коническую форму, обеспечивающую центровку их относительно обечайки при сборке. Ацетиленовый баллон (рис. 10.13 б) выполнен из более прочной низколегированной стали 15ХСНД, и нахлесточные соединения при его изготовлении недопустимы. Все рабочие соединения стыковые, причем кольцевые швы допускается выполнять на подкладках.
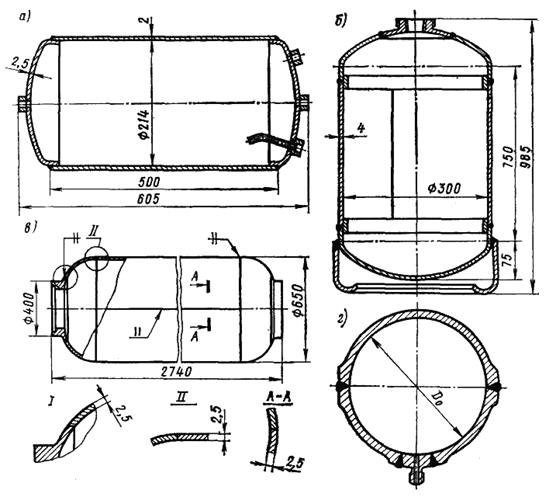
Рис.10.13. Тонкостенные сосуды:
а – тормозной резервуар грузового автомобиля; б – ацетиленовый баллон; в – сосуд высокого давления; г – шар-баллон из титанового сплава
При использовании высокопрочной стали 25ХСНВФА (σв =1400 МПа) подкладные кольца у стыковых соединений уже применять нельзя (рис. 10.13 в).
Иногда для понижения рабочих напряжений в зоне сварного соединения увеличивают толщину металла в местах расположения швов (рис. 10.13 г).
Напряжения в продольном шве цилиндрической части радиусом R с толщиной стенки s
σ =pR/s, (10.22)
а в поперечном шве
σ1=pR/(2s). (10.23)
Напряжения в сферической части радиуса Roс толщиной so составляют
σo =pRo /(2so). (10.24)
Действительная конструктивная прочность сосудов в результате концентрации напряжений может оказаться ниже предельной. Большое влияние оказывает отношение σт/σв. В случае если σт/σв=0,6 – 0,75, конструктивная прочность сосуда приближается к предельной. Если σт/σв=0,9, то конструктивная прочность может оказаться значительно меньше предельной.
Если в тонкостенном сосуде создается вакуум, то оболочки надо проверить на устойчивость. Цилиндрические оболочки при длине L<10r, где r -радиус цилиндра, проверяются по формуле
σкр=0,55Е r (s/r)3/2 /L, (10.25)
где σкр – критическое напряжение; s -толщина оболочки, Е – модуль упругости.
Устойчивость сферической оболочки определяется формулой
σкр=0,1 Es/r. (10.26)
Допускаемое напряжение [σ]≤ σкрm, где m=0,8 – коэффициент условий работы.
Тонкостенные сосуды в виде различных тормозных баллонов для наземного транспорта изготовляют крупными сериями, используя хорошо свариваемые материалы относительно невысокой прочности. Примером может служить воздушный тормозной резервуар железнодорожного вагона из углеродистой стали. Он имеет отбортованные днища, приваренные к обечайке стыковым соединением. Его выполняют либо на остающемся подкладном кольце (рис 10.14 а), либо с проточкой отбортованной части днища (рис 10.14 6).
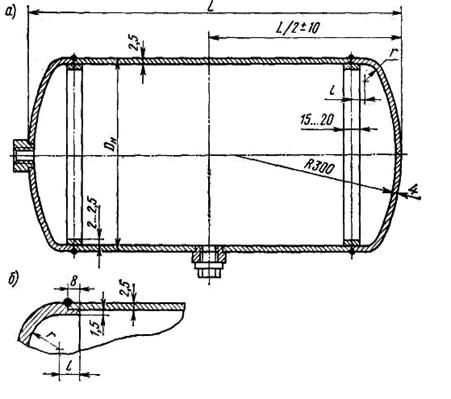
Рис.10.14. Воздушный тормозной резервуар железнодорожного вагона
Чем больше диаметр DH, тем более нагруженными оказываются резервуары; при расчете на прочность учитывают возможность уменьшения толщины стенок в результате коррозии на 0,7-1 мм. Коэффициент запаса прочности n = σв/ [σ]рпринимают не менее 3,5.
Сосуды со стенками средней толщины (до 40 мм) широко используются в химическом аппаратостроении, а также как емкости для хранения и транспортирования жидкостей и сжиженных газов. Нередко требуется защита рабочей поверхности аппарата от коррозионного воздействия среды и сохранение вязкости и пластичности материала несущих конструктивных элементов при низкой температуре. Поэтому используемые материалы весьма разнообразны: углеродистые и высоколегированные стали, медь, алюминий, титан и их сплавы. Так как для обеспечения необходимого срока службы аппарата достаточно иметь слой коррозионно-стойкого материала толщиной всего несколько миллиметров, то нередко используют двухслойный прокат. Аппаратуру емкостного типа обычно выполняют в виде цилиндрических сосудов. При избыточном давлении 0,4-1,6 МПа и выше, а также в емкостях, используемых для транспортировки жидкостей, соединения листовых элементов обечаек и днищ выполняют только стыковыми.
Барабаны котлов
В состав котельных агрегатов входят барабан, экономайзеры, пароперегреватели и камеры. Барабаны котлов высокой производительности имеют диаметры 1600-1800 мм, толщина их стенок достигает 100 мм. Барабан по длине состоит из отдельных обечаек; днища барабанов, как правило, штампованные. Все соединения выполняются электрошлаковой и дуговой сваркой.
Для котельных сосудов типа барабанов (рис. 10.15) характерно большое число штуцеров различного назначения.
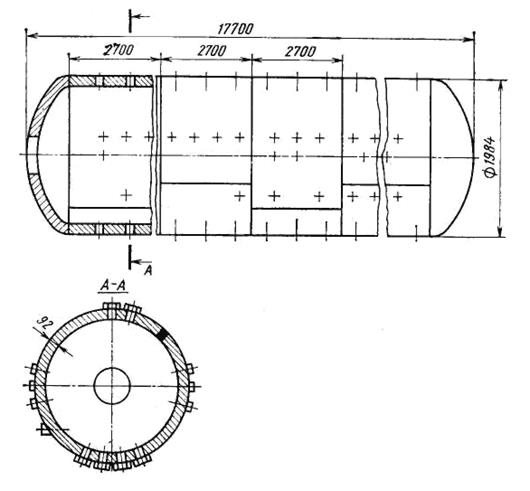
Рис.10.15. Общий вид сварного барабана котла
Поэтому при проектировании котельного оборудования большое внимание уделяют определению допустимого размера неукрепленного отверстия и расчету укрепления отверстий. Учет ослабления стенки отверстием осуществляют введением коэффициента φ. При продольном расположении отверстий
φпрод = (t – d)/ t, (10.27)
где t – расстояние между центрами отверстий в продольном направлении; d– диаметр отверстия.
Если диаметр отверстия превышает допускаемый (dпр), то должна быть увеличена толщина стенки сосуда или отверстие должно быть укреплено приваркой утолщенного штуцера или накладки (рис. 10.16).
В сосудах, работающих при температуре выше 300 °С при толщине обечайки более 40 мм, применение накладок не рекомендуется из-за опасности появления значительных температурных напряжений. Для них более рационально укрепление отверстия штуцером (рис. 10.16 б) или вваркой стыковым швом элемента большей толщины (рис. 10.16 г). Площадь сечения сварных швов fсв. присоединяющих штуцера или накладки к укрепляемому элементу, принимают без учета усиления.
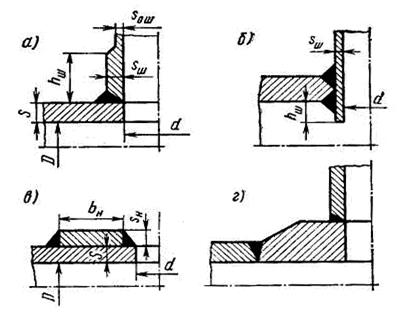
Рис.10.16. Типы укрепления отверстий сосудов: а – утолщенным штуцером; б – штуцером, не испытывающем давления; в – накладкой; г – вваркой утолщенного листа
Разделка под приварку штуцеров должна обеспечивать соединение их с барабаном или камерой по всей толщине штуцера. Разрешается приваривать штуцера без разделки, если при ручной дуговой сварке толщина их стенки не более 10 мм и при автоматической дуговой сварке под флюсом – не более 15 мм.
Рассмотренный метод расчета не учитывает влияния местной концентрации напряжений у отверстий. Полагают, что при высокой пластичности сталей появление местных небольших упругопластических деформаций не снижает работоспособности конструкций. При действии переменных нагрузок прочность сосудов может снижаться, особенно при использовании высокопрочных сталей (σв =800 – 900 МПа). Разрушения образуются в зонах концентрации напряжений: в местах приварки фланцев, труб, патрубков, штуцеров. Вероятность малоциклового разрушения заметно возрастает, когда в зоне концентрации оказываются дефекты.
Для надежной работы котлов и сосудов большое значение имеют пластические свойства металла и низкий уровень остаточных напряжений. Поэтому сварные конструкции котлов подвергают термической обработке. Для устранения остаточных напряжений в конструкциях из низкоуглеродистой стали достаточно высокого отпуска при T=600 – 650 °С.
Источник
Если толщина стенок цилиндра мала по сравнению с радиусами и , то известное выражение для тангенцальных напряжений приобретает вид
т. е. величину, определенную нами раньше (§ 34).
Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.
Выделим (Рис.1) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану.
Рис.1. Фрагмент тонкостенного резервуара и его напряженное состояние.
Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно и , радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим и , толщину стенки назовем t.
По симметрии по граням выделенного элемента будут действовать только нормальные напряжения в меридиальном направления и в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут и . Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.
Усилия (Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную
Рис.2. Равновесие элемента тонкостенного резервуара
Подобным же образом усилия дадут в том же направлении равнодействующую Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу
Отсюда
Это основное уравнение, связывающее напряжения и для тонкостенных сосудов вращения, дано Лапласом.
Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.
Рассмотрим случай гидростатической нагрузки (рис.3). Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х.
Рис.3. Равновесие нижнего фрагмента тонкостенного резервуара.
Каждая пара усилий , действующих на диаметрально противоположные элементы проведенного сечения, дает вертикальную равнодействующую bс, равную
сумма этих усилий, действующих по всей окружности проведенного сечения, будет равна ; она будет уравновешивать давление жидкости на этом уровне плюс вес жидкости в отрезанной части сосуда .
Отсюда
Зная уравнение меридиональной кривой, можно найти , х и для каждого значения у, и стало быть, найти , а из уравнения Лапласа и
Например, для конического резервуара с углом при вершине , наполненного жидкостью с объемным весом у на высоту h, будем иметь:
тогда
Для сферического сосуда радиусом , находящегося под внутренним давлением , по симметрии ; тогда из уравнения (Лапласа), так как
и
Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла , то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений по обе стороны точки перелома.
Дальше…
Источник
13.1. Понятие о безмоментной теории расчета тонкостенных сосудов
В инженерной практике
широкое применение находят такие
конструкции, как цистерны, водонапорные
резервуары, газгольдеры, воздушные и
газовые баллоны, купола зданий, аппараты
химического машиностроения, части
корпусов турбин и реактивных двигателей
и т.д. Все эти конструкции с точки зрения
их расчета на прочность и жесткость
могут быть отнесены к тонкостенным
сосудам (оболочкам) (Рис.13.1,а).
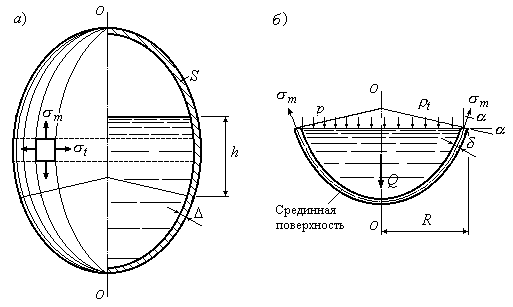
Рис.13.1
Характерной
особенностью большинства тонкостенных
сосудов является то, что по форме они
представляют тела вращения, т.е. их
поверхность может быть образована
вращением некоторой кривой
вокруг осиО–О.
Сечение сосуда плоскостью, содержащей
ось О–О,
называется меридиональным
сечением, а
сечения, перпендикулярные к меридиональным
сечениям, называются окружными.
Окружные сечения, как правило, имеют
вид конуса. Показанная на рис 13.1б нижняя
часть сосуда отделена от верхней окружным
сечением. Поверхность, делящая толщину
стенок сосуда пополам, называется
срединной
поверхностью.
Считается, что оболочка является
тонкостенной, если отношение наименьшего
главного радиуса кривизны в данной
точке поверхности к толщине стенки
оболочки превышает число 10
.
Рассмотрим
общий случай действия на оболочку
какой-либо осесимметричной нагрузки,
т.е. такой нагрузки, которая не меняется
в окружном направлении и
может
меняться лишь вдоль меридиана. Выделим
из тела оболочки двумя окружными и двумя
меридиональными сечениями элемент
(Рис.13.1,а).
Элемент
испытывает растяжение во взаимно
перпендикулярных направлениях и
искривляется. Двустороннему растяжению
элемента соответствует равномерное
распределение нормальных напряжений
по толщине стенки
и возникновение в стенке оболочки
нормальных усилий. Изменение кривизны
элемента предполагает наличие в стенке
оболочки изгибающих моментов. При изгибе
в стенке балки возникают нормальные
напряжения, меняющиеся по толщине
стенки.
При
действии осесимметричной нагрузки
влиянием изгибающих моментов можно
пренебречь, так как преобладающее
значение имеют нормальные силы. Это
имеет место тогда, когда форма стенок
оболочки и нагрузка на нее таковы, что
возможно равновесие между внешними и
внутренними усилиями без появления
изгибающих моментов. Теория расчета
оболочек, построенная на предположении,
что нормальные напряжения, возникающие
в оболочке, постоянны по толщине и,
следовательно, изгиб оболочки отсутствует,
называется безмоментной
теорией оболочек.
Безмоментная теория хорошо работает,
если оболочка не имеет резких переходов
и жестких защемлений и, кроме того, не
нагружена сосредоточенными силами и
моментами. Кроме того, эта теория дает
более точные результаты, чем меньше
толщина стенки оболочки, т.е. чем ближе
к истине предположение о равномерном
распределении напряжений по толщине
стенки.
При
наличии сосредоточенных сил и моментов,
резких переходов и защемлений сильно
усложняется решение задачи. В местах
крепления оболочки и в местах резких
изменений формы возникают повышенные
напряжения, обусловленные влиянием
изгибающих моментов. В этом случае
применяется так называемая моментная
теория расчета оболочек.
Следует отметить, что вопросы общей
теории оболочек выходят далеко за рамки
сопротивления материалов и изучается
в специальных разделах строительной
механики. В настоящем пособии при расчете
тонкостенных сосудов рассматривается
безмоментная теория для случаев, когда
задача определения напряжений, действующих
в меридиональном и окружном сечениях,
оказывается статически определимой.
13.2. Определение
напряжений в симметричных оболочках
по безмоментной теории. Вывод уравнения
Лапласа
Рассмотрим осесимметричную тонкостенную
оболочку, испытывающую внутреннее
давление от веса жидкости (Рис.13.1,а).
Двумя меридиональными и двумя окружными
сечениями выделим из стенки оболочки
бесконечно малый элемент и рассмотрим
его равновесие (Рис.13.2).
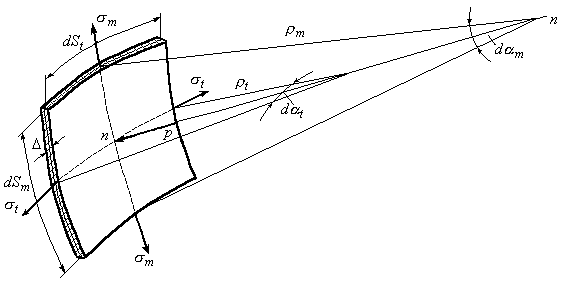
Рис.13.2
В
меридиональных и окружных сечениях
касательные напряжения отсутствуют
ввиду симметрии нагрузки и осутствия
взаимных сдвигов сечений. Следовательно,
на выделенный элемент будут действовать
только главные нормальные напряжения:
меридиональное напряжение
иокружное
напряжение
.
На основании безмоментной теории будем
считать, что по толщине стенки напряжения
и
распределены равномерно. Кроме того,
все размеры оболочки будем относить к
срединной поверхности ее стенок.
Срединная
поверхность оболочки представляет
собой поверхность двоякой кривизны.
Радиус кривизны меридиана в рассматриваемой
точки обозначим
,
радиус кривизны срединной поверхности
в окружном направлении обозначим
.
По граням элемента действуют силы
и
.
На внутреннюю поверхность выделенного
элемента действует давление жидкости
,
равнодействующая которого равна
.
Спроектируем приведенные выше силы на
нормаль
к поверхности:
.
(а)
Изобразим проекцию элемента на
меридиональную плоскость (Рис.13.3) и на
основании этого рисунка запишем в
выражении (а) первое слагаемое. Второе
слагаемое записывается по аналогии.
Заменяя в (а) синус его аргументом ввиду
малости угла и разделив все члены
уравнения (а) на
,
получим:
(б).
Учитывая, что кривизны меридионального
и окружного сечений элемента равны
соответственно
и
,
и подставляя эти выражения в (б) находим:
.
(13.1)
Выражение (13.1) представляет собой
уравнения Лапласа, названного так в
честь французского ученого, который
получил его в начале XIXвека при изучении
поверхностного натяжения в жидкостях.
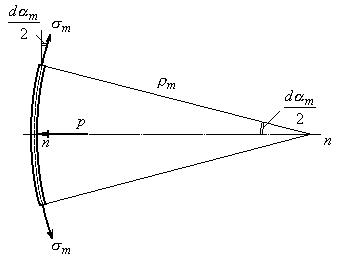
Рис.13.3
В уравнение (13.1) входят два неизвестных
напряжения
и
.
Меридиональное напряжение
найдем, составив уравнение равновесия
на ось
сил, действующих на отсеченную часть
оболочки (Рис.12.1,б). Площадь окружного
сечения стенок оболочки посчитаем по
формуле
.
Напряжения
ввиду симметрии самой оболочки и нагрузки
относительнго оси
распределены по площади равномерно.
Следовательно,
,
откуда
,
(13.2)
где
вес части сосуда
и жидкости, лежащих ниже рассматриваемого
сечения;
давление жидкости, по закону Паскаля
одинаковое во всех направлениях и равное
,
где
глубина рассматриваемого сечения, а
вес единицы объема
жидкости. Если жидкость хранится в
сосуде под некоторым избыточным в
сравнении с атмосферным давлением
,
то в этом случае
.
Теперь, зная напряжение
из уравнения Лапласа (13.1) можно найти
напряжение
.
При решении практических задач ввиду
того, что оболочка тонкая, можно вместо
радиусов срединной поверхности
и
подставлять радиусы наружной и внутренней
поверхностей.
Как уже отмечалось окружные и меридиональные
напряжения
и
являются главными напряжениями. Что
касается третьего главного напряжения,
направление которого нормально к
поверхности сосуда, то на одной из
поверхностей оболочки (наружной или
внутреннейв
зависимости от того, с какой стороны
действует давление на оболочку) оно
равно
,
а на противоположной – нулю. В тонкостенных
оболочках напряжения
и
всегда значительно больше
.
Это означает, что величиной третьего
главного напряжения можно пренебречь
по сравнению си
,
т.е. считать его равным нулю.
Таким образом, будем считать, что материал
оболочки находится в плоском напряженном
состоянии. В этом случае для оценки
прочности в зависимости от состояния
материала следует пользоваться
соответствующей теорией прочности.
Например, применив четвертую
(энергетическую) теорию, условие прочности
запишем в виде:
.
(13.3)
Рассмотрим несколько примеров расчета
безмоментнтых оболочек.
Пример 13.1.Сферический сосуд находится
под действием равномерного внутреннего
давления газа
(Рис.13.4).
Определить напряжения действущие в
стенке сосуда и оценить прочность сосуда
с использованием третьей теории
прочности. Собственным весом стенок
сосуда и весом газа пренебрегаем.
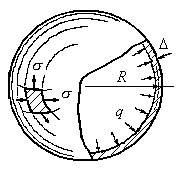
Рис.13.4
Решение:
1. Ввиду круговой симметрии оболочки и
осесимметричности нагрузки напряжения
и
одинаковы во всех точках оболочки.
Полагая в (13.1)
,
,
а
,
получаем:
.
(13.4)
2. Выполняем проверку по третьей теории
прочности:
.
Учитывая, что
,
,
,
условие прочности принимае вид:
.
(13.5)
Пример 13.2.Цилиндрическая оболочка
находится под действием равномерного
внутреннего давления газа
(Рис.13.5). Определить окружные и
меридиональные напряжения, действующие
в стенке сосуда, и оценить его прочность
с использованием четвертой теории
прочности. Собственным весом стенок
сосуда и весом газа пренебречь.
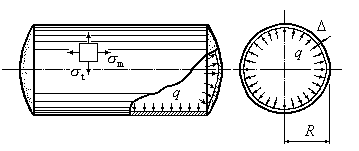
Рис.13.5
Решение:
1. Меридианами в цилиндрической части
оболочки являются образующие, для
которых
.
Из уравнения Лапласа (13.1) находим окружное
напряжение:
.
(13.6)
2. По формуле (13.2) находим меридиональное
напряжение, полагая
и
:
.
(13.7)
3. Для оценки прочности принимаем:
;
;
.
Условие прочности по четвертой теории
имеет вид (13.3). Подставляя в это условие
выражения для окружных и меридиональных
напряжений (а) и (б), получаем
.
(13.8)
Пример 12.3.Цилиндрический резервуар
с коническим днищем находится под
действием веса жидкости (Рис.13.6,б).
Установить законы изменения окружных
и меридиональных напряжений в пределах
конической и цилиндрической части
резервуара, найти максимальные напряжения
и
и построить эпюры распределения
напряжений по высоте резервуара. Весом
стенок резервуара пренебречь.
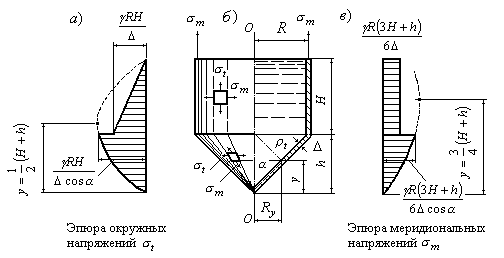
Рис.13.6
Решение:
1. Находим давление жидкости на глубине
:
.
(а)
2. Определяем окружные напряжения из
уравнения Лапласа, учитывая, что радиус
кривизны меридианов (образующих)
:
.
(б)
Для конической части оболочки
;
.
(в)
Подставляя (в) в (б) получим закон изменения
окружных напряжений в пределах конической
части резервуара:
.
(13.9)
Для цилиндрической части, где
закон распределения окружных напряжений
имеет вид:
.
(13.10)
Эпюра
показана на рис.13.6,а. Для конической
части эта эпюра параболическая. Ее
математический максимум имеет место в
середине общей высоты при
.
При
он имеет условное значение, при
максимум напряжений попадает в пределы
конической части и имеет реальное
значение:
.
(13.11)
3. Определяем меридиональные напряжения
.
Для конической части вес жидкости в
объме конуса высотой
равен:
.
(г)
Подставляя (а), (в) и (г) в формулу для
меридиональных напряжений (13.2) , получим:
.
(13.12)
Эпюра
показана на рис.13.6,в. Максимум эпюры
,
очерченной для конической части также
по параболе, имеет место при
.
Реальное значение он имеет при
,
когда попадает в пределы конической
части. Максимальные меридиональные
напряжения при этом равны:
.
(13.13)
В цилиндрической части напряжение
по высоте не меняется и равно напряжению
у верхней кромки в месте подвеса
резервуара:
.
(13.14)
В местах, где поверхность резервуара
имеет резкий излом, как, например, в
месте перехода от цилиндрической части
к конической (Рис.13.7) (Рис.13.5), радиальная
составляющая меридиональных напряжений
не уравновешена (Рис.13.7).
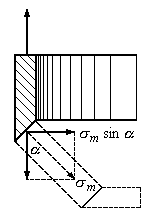
Рис.13.7
Эта составляющая по периметру кольца
создает радиальную распределенную
нагрузку интенсивностью
,
стремящуюся согнуть кромки цилиндрической
оболочки внутрь. Для устранения этого
изгиба ставится ребро жесткости
(распорное кольцо) в виде уголка или
швеллера, опоясывающего оболочку в
месте перелома. Это кольцо воспринимает
радиальную нагрузку
(Рис.13.8,а).
Вырежем двумя бесконечно близко
расположенными радиальными сечениями
из распорного кольца его часть (Рис.13.8,б)
и определим внутренние усилия, которые
в нем возникают. В силу симметрии самого
распорного кольца и нагрузки, распределенной
по его контуру, поперечная сила и
изгибающий момент в кольце не возникают.
Остается только продольная сила
.
Найдем ее.
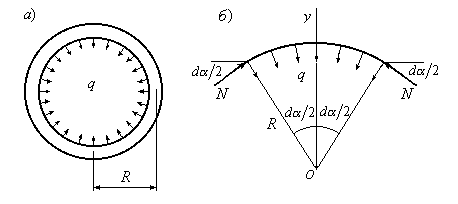
Рис.13.8
Составим сумму проекций всех сил,
действующих на вырезанный элемент
распорного кольца, на ось
:
.
(а)
Заменим синус угла
углом ввиду его малости
и подставим в (а). Получим:
,
откуда
(13.15)
Таким образом, распорное кольцо работает
на сжатие. Условие прочности принимает
вид:
,
(13.16)
где
радиус срединной
линии кольца;
площадь поперечного
сечения кольца.
Иногда вместо распорного кольца создают
местное утолщение оболочки, загибая
края днища резервуара внутрь обечайки.
Если оболочка испытывает внешнее
давление, то меридиональные напряжения
будут сжимающими и радиальное усилие
станет отрицательным, т.е. направленным
наружу. Тогда кольцо жесткости будет
работать не на сжатие, а на растяжение.
При этом условие прочности (13.16) останется
таким же.
Следует отметить, что постановка кольца
жесткости полностью не устраняет изгиба
стенок оболочки, так как кольцо жесткости
стесняет расширение колец оболочки,
примыкающих к ребру. В результате
образующие оболочки вблизи кольца
жесткости искривляются. Явление это
носит название краевого эффекта. Оно
может привести к значительному местному
возрастанию напряжений в стенке оболочки.
Общая теория учета краевого эффекта
рассматривается в специальных курсах
с помощью моментной теории расчета
оболочек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник