Объем цилиндрического сосуда формула

Ââåäèòå ðàäèóñ îñíîâàíèÿ è âûñîòó öèëèíäðà | |
| Ðàäèóñ: | |
| Âûñîòà: | |
Öèëèíäð – ãåîìåòðè÷åñêîå òåëî, êîòîðîå ïîëó÷àåòñÿ ïðè âðàùåíèè ïðÿìîóãîëüíèêà âîêðóã åãî ñòîðîíû. Ôîðìóëà îáúåìà öèëèíäðà: , ãäå R – ðàäèóñ îñíîâàíèé, h – âûñîòà öèëèíäðà | |
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Ìû â ñîöñåòÿõ Ïðèñîåäèíÿéòåñü! Íàøëè îøèáêó? Åñòü ïðåäëîæåíèÿ? Ñîîáùèòå íàì |
Ýòîò êàëüêóëÿòîð ìîæíî âñòàâèòü íà ñàéò, â áëîã Ñîçäàäèì êàëüêóëÿòîð äëÿ âàñ |
Источник
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
– Вычисления (показано)
(скрыто)
– примечания (показано)
(скрыто)
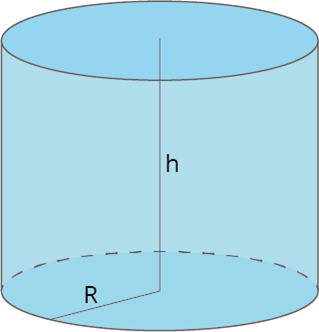
r – радиус основания цилиндра
h – высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

S – площадь основания цилиндра
h – высота цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d – диаметр основания цилиндра
h – высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Объем цилиндрической полости
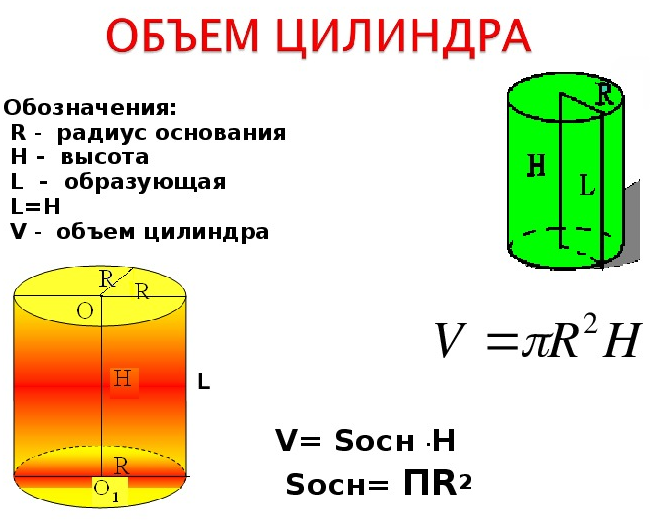
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным .
.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
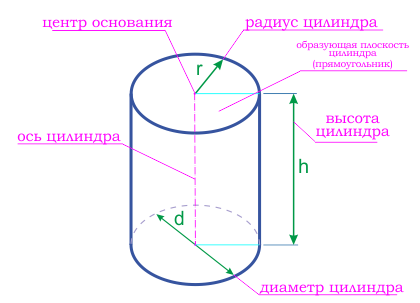
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Поверхности цилиндра
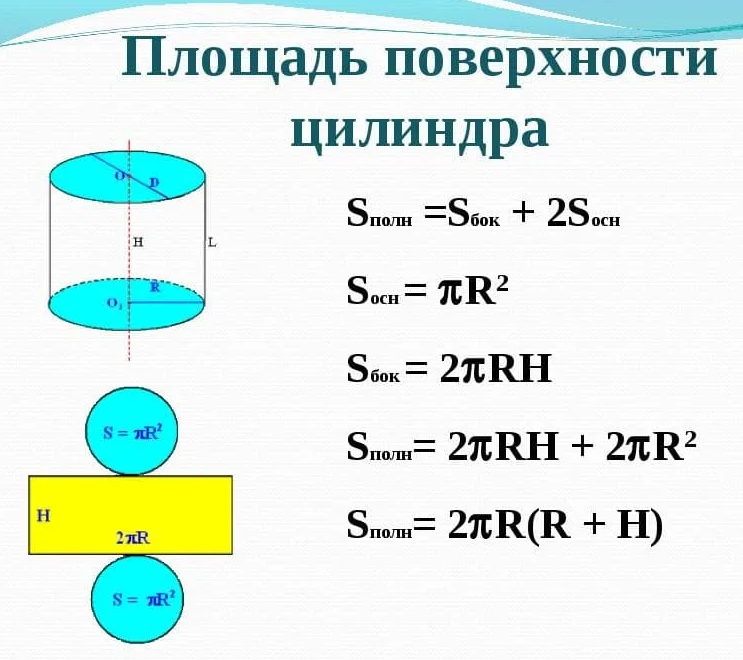
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса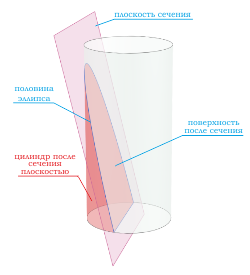 .
.
Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Источник
Цилиндр — геометрическое тело, получаемое при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор объема цилиндра
Это определение самого простого, так называемого, прямого кругового цилиндра. Более полное и общее определение цилиндра следующее:
Цилиндром называют геометрическое тело, которое получается путем пересечения двух плоскостей, которые параллельны друг другу, с прямыми, которые так же параллельны друг другу.
Эти прямые получили название образующих цилиндра. Плоскости – это основания цилиндра.
Прямая, которая перпендикулярна плоскостям, содержащим основания цилиндра, называется высотой данного цилиндра.
Типы цилиндров
Они зависят от того, под каким углом пересекаются основания и образующие цилиндра. Если угол равен 90 градусам, тогда цилиндр называется прямым. Линия, которая соединяет центр одного основания с другим, называется осью симметрии. Если угол не прямой, то цилиндр называется наклонным (косым).
Если форма основания цилиндра — гипербола, то цилиндр гиперболический, если парабола, круг или эллипс, то, соответственно параболический, круговой и эллиптический.
Формула объема кругового цилиндра
Для того, чтобы вычислить объем прямого кругового цилиндра нужно просто умножить площадь его основания (то есть, площадь круга, лежащего в основании цилиндра) на высоту этого цилиндра.
Формула объема кругового цилиндра
V=Sосн⋅hV=S_{text{осн}}cdot hV=Sосн⋅h
SоснS_{text{осн}}Sосн — площадь основания цилиндра;
hhh — высота этого цилиндра.
Для кругового цилиндра, площадь основания SоснS_{text{осн}}Sосн это площадь круга:
Sосн=π⋅R2S_{text{осн}}=picdot R^2Sосн=π⋅R2
RRR — радиус круга.
Рассмотрим несколько примеров.
Задача 1
Найдите объем цилиндра, если площадь его основания равна 196π см2196pitext{ см}^2196π см2, а его высота hhh в 2 раза больше радиуса основания RRR.
Решение
Sосн=196πS_{text{осн}}=196piSосн=196π
h=2⋅Rh=2cdot Rh=2⋅R
Сначала вычисляем радиус основания:
Sосн=π⋅R2S_{text{осн}}=picdot R^2Sосн=π⋅R2
Выразим отсюда радиус RRR:
R2=SоснπR^2=frac{S_{text{осн}}}{pi}R2=πSосн
R=SоснπR=sqrt{frac{S_{text{осн}}}{pi}}R=πSосн
R=196ππR=sqrt{frac{196pi}{pi}}R=π196π
R=196R=sqrt{196}R=196
R=14R=14R=14
По условию задачи, высота цилиндра в два раза больше RRR:
h=2⋅R=2⋅14=28h=2cdot R=2cdot 14=28h=2⋅R=2⋅14=28
Тогда объем цилиндра по формуле:
V=Sосн⋅h=196⋅π⋅28≈17232 см3V=S_{text{осн}}cdot h=196cdotpicdot28approx17232text{ см}^3V=Sосн⋅h=196⋅π⋅28≈17232 см3
Ответ
17232 см3.17232text{ см}^3.17232 см3.
Задача 2
Определить, чему равен объем цилиндра, если радиус его основания RRR равен 7 см7text{ см}7 см, а высота – 14 см14text{ см}14 см.
Решение
R=7R=7R=7
h=14h=14h=14
По формуле для объема цилиндра получаем:
V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3V=S_{text{осн}}cdot h=picdot R^2cdot h=picdot7^2cdot14approx2154text{ см}^3V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3
Ответ
2154 см3.2154text{ см}^3.2154 см3.
Задача 3
В квадрат со стороной aaa равной 4 см4text{ см}4 см вписана окружность, являющаяся основанием цилиндра, высота которого равна 20 см20text{ см}20 см. Вычислите его объем.
Решение
a=4a=4a=4
h=20h=20h=20
Исходя из того, что сторона квадрата, в который вписана окружность, равна диаметру DDD этой окружности, можно найти площадь основания цилиндра:
Sосн=π⋅R2=π⋅D24=π⋅a24=π⋅424≈12.56S_{text{осн}}=picdot R^2=frac{picdot D^2}{4}=frac{picdot a^2}{4}=frac{picdot 4^2}{4}approx12.56Sосн=π⋅R2=4π⋅D2=4π⋅a2=4π⋅42≈12.56
Объем цилиндра:
V=Sосн⋅h≈12.56⋅20=251.2 см3V=S_{text{осн}}cdot happrox12.56cdot20=251.2text{ см}^3V=Sосн⋅h≈12.56⋅20=251.2 см3
Ответ
251.2 см3.251.2text{ см}^3.251.2 см3.
Тест по теме «Объем цилиндра»
Источник
Цилиндр – это объемное тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают. Цилиндр (от греческого «kulindros» — ролик, каток) относится к основным геометрическим фигурам. В элементарных математических трактовках, он определяется как трехмерное тело. Объем цилиндра – один из базовых параметров, который необходимо уметь вычислять каждому человеку. Формула применяется во многих сферах промышленности, а также в строительстве, архитектуре, механике, программировании.
Объем цилиндра по высоте и радиусу

Узнать объем полой фигуры можно моментально, воспользовавшись удобной онлайн-программой. Сервис позволяет за секунды вычислить параметры тела и получить результаты в кубических сантиметрах, метрах, литрах. Расчет производится по двум математическим формулам:
- По высоте и радиусу: V = S х h.
- Объём по площади основания и высоте: V = ∏ х R2 х h
Где V – объем, S – площадь, h – высота. Чтобы рассчитать объем необходимо площадь основания тела умножить на h. Следовательно, для этого необходимо знать две переменные.
R – радиус, возведенный в квадрат. От первой формулы, расчет отличается тем, что сначала необходимо найти значение радиуса. Для этого диаметр делится на 2 или применяется формула S/2 х ∏ х H. ∏ – константа 3,14 (отношение длины окружности к диаметру).
Объём цилиндра через площадь основания и высоту

Ответы:
Программа позволяет определить объем тела по обеим формулам. Для этого необходимо только подставить цифры в соответствующие строки и нажать кнопку рассчитать. Пошаговая инструкция вычисления базовых показателей фигуры на калькуляторе по высоте и радиусу:
- в графе «h» ввести длину заданной фигуры, рядом выбрать метрику – в миллиметрах, сантиметрах, метрах;
- в строке «r» ввести радиус тела и выбрать меру длины (мм, см, м);
- в графе «Результат» определить, в чем будет выведен V – кубах, литрах.
[ads-pc-2][ads-mob-2]
Например, длина фигуры составляет 1,6 метра, радиус 25 сантиметров. Объем равен 314.2 литров, 314200 куб. см или 0.314 куб. м. Результат выводится моментально, с точностью до тысячной. Правильность вычисления зависит только от достоверности исходных данных.
Где применяется программа
Сервис разработана для всех пользователей, чья профессиональная деятельность предполагает решение математических задач. Калькулятор будет полезен школьникам 5-9 классов, учащимся 11 классов в подготовительном процессе к ЕГЭ и контрольным срезам, а также родителям для проверки правильности решения задач.
С помощью сервиса можно решить типичные тестовые задания школьной программы, подставляя известные значения и не забывая выставлять метрические параметры (в кубических сантиметрах, кубометрах, миллиметрах, литрах). Например:
- Дан цилиндр, с площадью основания 58,3 см2 и высотой 7 см. Чтобы посчитать V следует воспользоваться расчетом через площадь и высоту.
- Дан цилиндр длиной 11 см и диаметром основания 16 см. Параметры тела следует вычислять в первом калькуляторе «V по высоте и радиусу».
Решение: V = 58,3 см2 х 7 см = 408.1 см³ или 0.408 л.
Вычисление: перед использованием программы следует определить радиус основания – 16см/2 = 8 см. Затем значения подставить в нужные поля. Расчет производится на основании формулы V = 3,14 х 82 х 11 см = 2211.968 см³.
Следует учитывать, что параметры полого горизонтального, наклонного, косого, кругового, равностороннего цилиндров вычисляются с использованием дополнительных формул.
[ads-pc-3][ads-mob-3]
Теоретические знания необходимы, чтобы найти площадь основания или диаметр. Для этого достаточно вспомнить уроки геометрии за 5 класс по теме «Цилиндр» и применять на практике простейшие расчеты.
Источник
1. Расчет объема куба
a – сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):
4. Как вычислить объем цилиндра ?
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):
5. Как найти объем конуса ?
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8. Объем правильного тетраэдра
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
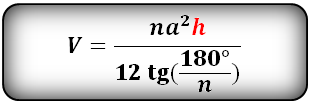
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
12. Расчет объема пирамиды
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
13. Расчёт объёма усечённой пирамиды
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):
14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
15. Объем шарового сектора
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):
16. Объем шарового слоя
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
Источник
