Обьем детали в сосуде

В
заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о
погружении детали в жидкость или о переливании жидкости из одного сосуда
в другой.
Вопросы
в условии связаны с нахождением объёма погружаемого в жидкость тела или
с нахождением какого-либо параметра сосуда. Форма сосуда может быть
различной: цилиндр, призма.
Что необходимо понимать?
Если
жидкость залита в цилиндрический сосуд, то она принимает форму
цилиндра. Если она залита в имеющий форму призмы, то соответственно
принимает форму призмы. Это означает, что формулы для объёмов цилиндра и
призмы работают и для объёмов жидкостей помещённых в такие сосуды.
Формула объёма (цилиндра и призмы):
Если
жидкость перливается в аналогичный сосуд с меньшим основанием, уровень
(высота) жидкости увеличивается; если в сосуд с большим основанием, то
уровень жидкости уменьшается.
Рекомендации!
В
задачах на погружение детали в жидкость следует найти объём полученный
после её погружения, далее найти разность объёмов до и после (если
данные в условии это позволяют). Можно такие задачи решать и другим
способом, используя закон Архимеда. Примеры рассмотрены ниже.
В
задачах, где идёт речь о переливании жидкости в другой сосуд (с
уменьшенной или увеличенной площадью основания) помните о том, что сам
объём жидкости остаётся неизменным. Вы можете выразить его через площадь
основания и высоту (S1 и H1) одного сосуда и площадь основания и высоту (S2 и H2) другого сосуда, далее полученные выражения приравнять.
При
дальнейших преобразованиях получите отношение соответствующих величин –
либо площадей оснований, их рёбер, либо высот. Пример такой задачи
рассмотрен ниже в статье.
В цилиндрический сосуд налили 5000 см3
воды. Уровень жидкости оказался равным 40 см. В воду полностью
погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см.
Чему равен объем детали? Ответ выразите в см3.
Мы знаем, что объём цилиндра равна произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Высота это есть уровень жидкости.
Итак, из имеющихся данных можем найти площадь основания:
Основание
цилиндра у нас величина неизменная, но изменилась высота жидкости (при
погружении детали) на 15 сантиметров, то есть она стала
40 +15 = 55 см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 6875 – 5000 = 1875 см3
Можно решать подобные задачи более рациональным способом.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/45 исходного объема:
Ответ: 1875
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см3 воды
и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали?
Ответ выразите в см3.
Принцип решения тот же самый, что и в предыдущей задаче.
Мы знаем, что объём призмы равен произведению площади основания на высоту:
В
жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы
вычислить объём детали необходимо из полученного объёма (полученного
после погружения детали) вычесть объём жидкости, который был изначально.
Из имеющихся данных можем найти площадь основания призмы:
Основание призмы не изменилось, но изменилась высота жидкости (при погружении детали) она стала 24см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 3000 – 2500 = 500 см3
Второй способ:
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20 исходного объема:
Ответ: 500
Решить самостоятельно:
Посмотреть решение
В
сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 250 см. На какой высоте будет находиться уровень
воды, если ее перелить в другой такой же сосуд, у которого сторона
основания в 5 раз больше, чем у первого? Ответ выразите в см.
В
подобных задачах с переливаниями жидкости следует помнить, что объём её
остаётся прежним (он не изменен – куда бы её не перелили).
Объем
жидкости в данном случае это объём правильной треугольной призмы (в
её основании лежит правильный треугольник). Он равен произведению
площади основания призмы на высоту:
Суть
дальнейших действий сводится к тому, что мы можем выразить объёмы
жидкостей в двух призмах: первой и второй (основание которой в 4 раза
больше), а затем приравнять полученные выражения, в итоге после
преобразований получим отношение двух высот.
Естественно, что высота жидкости уменьшится, если увеличить площадь основания.
Обозначим исходную высоту жидкости Н1, полученную после переливания Н2.
Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:
Таким образом, объём залитой жидкости в первую призму равен:
Площадь основания второй призмы равна:
Объём залитой жидкости во вторую призму равен:
Найдём отношение высот:
Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.
Или можно сказать так:
При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.
Ответ: 10
Решить самостоятельно:
Посмотреть решение
В
цилиндрический сосуд, в котором находится 14 литров воды, опущена
деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему
равен объем детали? Ответ выразите в литрах.
Объём цилиндра равна произведению площади его основания на высоту:
Жидкость в сосуде имеет цилиндрическую объёмную форму.
Уровень
жидкости поднялся в 1,1 раза – означает, что высота цилиндра
увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что
при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также
в 1,1 раза (так как зависимость величин прямопропорциональная).
Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.
Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.
Ответ: 1,4
Решить самостоятельно:
Посмотреть решение
Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?
Например,
если дан начальный объём и высота жидкости (в сосуде формы призмы или
цилиндра), то мы можем найти площадь основания. Затем, зная площадь
основания и высоту жидкости после погружения детали мы можем найти
полученный объём.
Далее
найти разницу между объёмами не составит труда (это относится к первым
двум задачам). В последней задаче для решения требуется немного
логики.
Источник
Задачи на плотность, массу и объем с решением
Формулы, используемые в задачах по физике на плотность, массу и объем.
Название величины | Обозначение | Единицы измерения | Формула |
Масса | m | кг | m = p * V |
Объем | V | м3 | V = m / p |
Плотность | p | кг/м3 | p = m / V |
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Найдите плотность молока, если 206 г молока занимают объем 200 см3?

Задача № 2.
Определите объем кирпича, если его масса 5 кг?

Задача № 3.
Определите массу стальной детали объёмом 120 см3
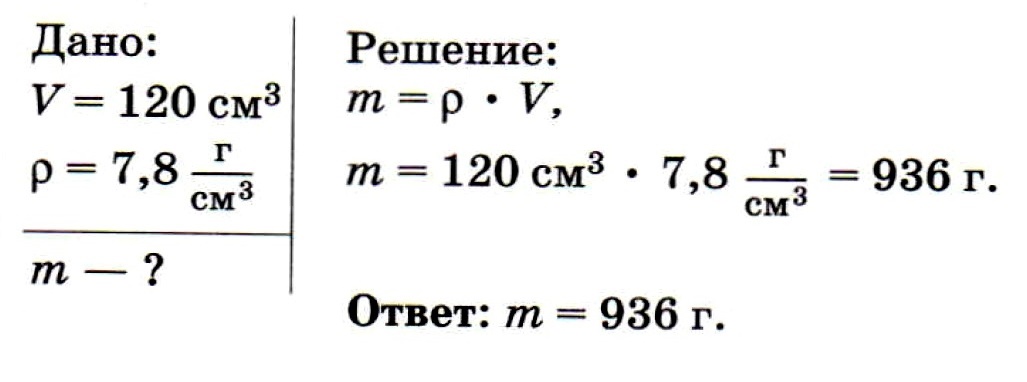
Задача № 4.
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5.
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.

Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6.
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7.
Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.
Задача № 8 (повышенной сложности).
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
РЕШЕНИЕ: Объем кубика VK = а3 = 216 см3. Объем стенок VС можно вычислить, зная массу кубика mК и плотность меди р: VС = mК / р = 91 см3. Следовательно, объем полости VП = VK — VC = 125 см3. Поскольку 125 см3 = (5 см)3, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.
Задача № 9 (олимпиадный уровень).
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.
Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Конспект урока «Задачи на плотность, массу и объем с решением».
Следующая тема: «Задачи на силу тяжести и вес тела».
Источник
Задание 1. В цилиндрическом сосуде уровень
жидкости достигает 48 см. На какой высоте
будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2
раза больше диаметра первого? Ответ выразите в см.
Решение. Заметим, что при переливании жидкости
из одного сосуда в другой объём жидкости не изменился. Объём цилиндра равен произведению
площади основания на высоту этого цилиндра. То есть V=Sh=pR2h. Поскольку в новом сосуде диаметр, а значит и
радиус, в 2 раза больше, то площадь основания будет больше в 4 раза, значит
высота, соответственно, уменьшится в 4 раза, то есть станет равна 48:4=12 см.
Ответ 12.
Задание 2. В
цилиндрический сосуд, в котором находится 6 дм3 воды, опустили
деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен
объём детали? Ответ выразите в дм3.
Решение. Заметим, что при опускании детали в
сосуд изменение общего объёма равно объёму детали. Объём цилиндра равен
произведению площади основания на высоту этого цилиндра. То есть V=Sh=pR2h. Так как уровень жидкости поднялся в 1,5 раза,
значит объём увеличился тоже в 1,5 раза и стал равен 6*1,5 = 9. Объём детали
равен 9 – 6=3.
Ответ 3.
Задания для самостоятельного решения. Все задания взяты из открытого банка заданий ФИПИ.
1.
В цилиндрическом сосуде уровень жидкости достигает
98 см. На какой высоте будет находиться уровень жидкости, если её перелить
во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра
первого? Ответ выразите в сантиметрах.
2. В цилиндрическом сосуде уровень
жидкости достигает 27 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3
раза больше диаметра первого? Ответ выразите в сантиметрах.
3. В цилиндрическом сосуде уровень
жидкости достигает 256 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8
раз больше диаметра первого? Ответ выразите в сантиметрах.
4.
В цилиндрическом сосуде уровень жидкости достигает
64 см. На какой высоте будет находиться уровень жидкости, если её перелить
во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра
первого? Ответ выразите в сантиметрах.
5. В цилиндрическом сосуде уровень
жидкости достигает 96 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4
раза больше диаметра первого? Ответ выразите в сантиметрах.
6. В цилиндрическом сосуде уровень
жидкости достигает 20 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2
раза больше диаметра первого? Ответ выразите в сантиметрах.
7. В цилиндрическом сосуде уровень
жидкости достигает 25 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5
раз больше диаметра первого? Ответ выразите в сантиметрах.
8. В цилиндрическом сосуде уровень
жидкости достигает 80 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4
раза больше диаметра первого? Ответ выразите в сантиметрах.
9. В цилиндрическом сосуде уровень
жидкости достигает 405 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9
раз больше диаметра первого? Ответ выразите в сантиметрах.
10. В цилиндрическом
сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться
уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 5 раз меньше диаметра первого? Ответ выразите в сантиметрах.
11. В цилиндрическом сосуде уровень
жидкости достигает 45 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3
раза больше диаметра первого? Ответ выразите в сантиметрах.
12. В цилиндрическом сосуде уровень
жидкости достигает 18 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3
раза больше диаметра первого? Ответ выразите в сантиметрах.
13. В цилиндрическом сосуде уровень
жидкости достигает 294 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7
раз больше диаметра первого? Ответ выразите в сантиметрах.
14. В цилиндрическом сосуде уровень
жидкости достигает 192 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8
раз больше диаметра первого? Ответ выразите в сантиметрах.
15. В цилиндрическом сосуде уровень
жидкости достигает 147 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7
раз больше диаметра первого? Ответ выразите в сантиметрах.
16. В цилиндрическом сосуде уровень
жидкости достигает 50 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5
раз больше диаметра первого? Ответ выразите в сантиметрах.
17. В цилиндрическом сосуде уровень
жидкости достигает 320 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8
раз больше диаметра первого? Ответ выразите в сантиметрах.
18. В цилиндрическом сосуде уровень
жидкости достигает 125 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5
раз больше диаметра первого? Ответ выразите в сантиметрах.
19. В цилиндрическом
сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться
уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 6 раз меньше диаметра первого? Ответ выразите в сантиметрах.
20. В цилиндрическом
сосуде уровень жидкости достигает 5 см. На какой высоте будет находиться
уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
21. В цилиндрическом
сосуде уровень жидкости достигает 6 см. На какой высоте будет находиться
уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 7 раз меньше диаметра первого? Ответ выразите в сантиметрах.
22. В цилиндрическом сосуде уровень
жидкости достигает 16 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2
раза больше диаметра первого? Ответ выразите в сантиметрах.
23. В цилиндрическом сосуде уровень
жидкости достигает 112 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4
раза больше диаметра первого? Ответ выразите в сантиметрах.
24. В цилиндрическом сосуде уровень
жидкости достигает 32 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4
раза больше диаметра первого? Ответ выразите в сантиметрах.
25. В цилиндрическом сосуде уровень
жидкости достигает 63 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3
раза больше диаметра первого? Ответ выразите в сантиметрах.
26. В цилиндрическом сосуде уровень жидкости
достигает 384 см. На какой высоте будет находиться уровень жидкости, если
её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше
диаметра первого? Ответ выразите в сантиметрах.
27. В цилиндрическом сосуде уровень
жидкости достигает 12 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2
раза больше диаметра первого? Ответ выразите в сантиметрах.
28. В цилиндрическом сосуде уровень
жидкости достигает 28 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2
раза больше диаметра первого? Ответ выразите в сантиметрах.
29. В цилиндрическом сосуде уровень
жидкости достигает 72 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6
раз больше диаметра первого? Ответ выразите в сантиметрах.
30. В цилиндрическом сосуде уровень
жидкости достигает 216 см. На какой высоте будет находиться уровень жидкости,
если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз
больше диаметра первого? Ответ выразите в сантиметрах.
31. В цилиндрическом
сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться
уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
32. В цилиндрическом сосуде уровень
жидкости достигает 567 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9
раз больше диаметра первого? Ответ выразите в сантиметрах.
33. В цилиндрическом сосуде уровень
жидкости достигает 144 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6
раз больше диаметра первого? Ответ выразите в сантиметрах.
34. В цилиндрическом сосуде уровень
жидкости достигает 324 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9
раз больше диаметра первого? Ответ выразите в сантиметрах.
35. В цилиндрическом сосуде уровень
жидкости достигает 243 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9
раз больше диаметра первого? Ответ выразите в сантиметрах.
36. В цилиндрический
сосуд, в котором находится 10 дм3 воды, опустили деталь. При
этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали?
Ответ выразите в дм3.
37. В цилиндрический
сосуд, в котором находится 4 дм3 воды, опустили деталь. При
этом уровень жидкости в сосуде поднялся в 2,5 раза. Чему равен объём детали?
Ответ выразите в дм3.
38. В цилиндрический
сосуд, в котором находится 8 дм3 воды, опустили деталь. При
этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали?
Ответ выразите в дм3.
39. В
цилиндрический сосуд налили 500 куб. см воды. В воду полностью
погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза.
Найдите объём детали. Ответ выразите в куб. см.
Источник
