Объем сосуда с идеальным газом увеличили
 |
Инструкция по выполнению работы
В заданиях В1–В4 требуется указать последовательность цифр, соответствующих правильному ответу. Эту последовательность следует внести в поле ответов без пробелов и других символов. (Цифры в ответе могут повторяться.)
Желаем успеха!
Здесь приведены справочные данные, которые могут понадобиться вам при выполнении работы.
При ознакомлении с Демонстрационным вариантом следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене, приведен в кодификаторе, помещённом на сайтах www.ege.edu.ru и www.fipi.ru.
B1. Объём сосуда с идеальным газом увеличили вдвое, выпустив половину газа и поддерживая температуру в сосуде постоянной. Как изменились при этом давление газа в сосуде, его плотность и внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
B2. В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
B3. Груз, привязанный к нити, отклонили от положения равновесия и отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
 | 1) координата х |
| 2) проекция скорости vх | |
| 3) кинетическая энергия Ек | |
| 4) потенциальная энергия Еп |
ОТВЕТЫ:
A:
B4. На рисунке изображена упрощённая диаграмма энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какие из этих четырёх переходов связаны с поглощением кванта света с наименьшей энергией и излучением света наименьшей длины волны? Установите соответствие между процессами поглощения и испускания света и стрелками, указывающими энергетические переходы атома.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕСС | ЭНЕРГЕТИЧЕСКИЙ ПЕРЕХОД |
| А) поглощение кванта света с наименьшей энергией | 1) 1 |
| 2) 2 | |
| Б) излучение света наименьшей длины волны | 3) 3 |
| 4) 4 |
ОТВЕТЫ:
A:
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.5%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический. Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V-2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Ответ: 0.32
Показать решение
Полный курс
Задача 2
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Ответ: 308
Показать решение
Полный курс
Задача 3
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
${tableP_1V={m}/{M}·RT_1; P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Ответ: 0.09
Показать решение
Полный курс
Задача 4
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Ответ: 1.5
Показать решение
Полный курс
Задача 5
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
${tableP_1=n_1·K·T_1; P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Ответ: 100
Показать решение
Полный курс
Задача 6
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
${tableP_1={2}/{3}·n_1·E_{к_1}; P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Ответ: 75
Показать решение
Полный курс
Задача 7
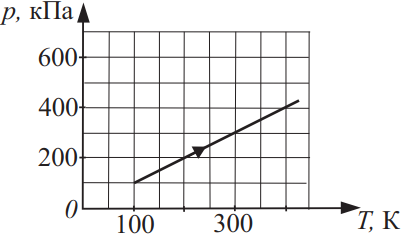
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Ответ: 83
Показать решение
Полный курс
Задача 8
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_0-?$
Решение:
${P_1}/{T_1} > {P_2}/{T_2}$ – изохорный.
$T_0={P_1}/{P_2}·T_2=3(1-200)$
$2T_0=600$
$T_0=300K$
Ответ: 300
Показать решение
Полный курс
Задача 9
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7{кг}/м^3$.
Ответ: 1.7
Показать решение
Полный курс
Задача 10
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К).
Решение
Дано:
$N_2T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$P=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клайперона $pV={m}/{M}R·T; T={pv·M}/{m·R}$
$T={0.2·10^6·8.31·0.028}/{4·10^{-3}·8.31}=140K$
Ответ: 140
Показать решение
Полный курс
Задача 11
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T_1=T_2-T_1={μ}/{3R}·(υ_2^2·r_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-r_1^2}={1}/{3200}$
Тогда $∆T_2={μ}/{3R}(υ_2^2-υ_3^2)={1}/{3200}(400^2-600^2)=62.5K$
Ответ: 62.5
Показать решение
Полный курс
Задача 12
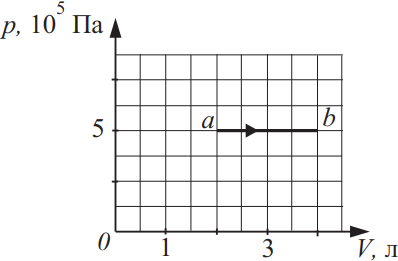
Идеальный газ в количестве 1,5 моль совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: ${tableP·V_a=vRT_a(1); P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Ответ: 160.45
Показать решение
Полный курс
Задача 13
Концентрация молекул идеального одноатомного газа равна 2 · 1024 м−3. Какое давление оказывает газ на стенки сосуда, если при этом средняя кинетическая энергия молекулы равна 1,5 · 10−20 Дж? Ответ выразите в (кПа).
Решение
Дано:
$n=2·10^{24}м^{-3}$
$E_к=1.5·10^{-20}$
$P-?$
Решение:
${tableE_к={3}/{2}KT={3}/{2}K{P}/{nK}; P=nKT;$
Выразим и получим формулу из основ МКТ: $p={E_к·2n}/{3}={1.5·10^{-20}·2·2·10^{24}}/{3}=20$кПа.
Ответ: 20
Показать решение
Полный курс
Задача 14
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Ответ: 1.56
Показать решение
Полный курс
Задача 15
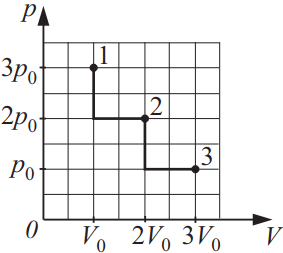
На диаграмме pV изображены процессы перевода некоторой неизменной массы идеального газа из состояния 1 в состояние 3. Начальная (T1) и конечная (T3) температуры связаны между собой соотношением T3/T1…
Решение
Дано:
$Т_1-$начальная
$Т_2$конечная
${T_3}/{T_1}-?$
Решение:
Запишем уравнение Менделеева-Клайперона для начальной и конечной точки состояния: ${table.{p_1·V_1}/{T_1}=υR; .{p_3·V_3}/{T_3}=υR;$.
$⇒{p_1·V_1}/{T_1}={p_3·V_3}/{T_3}⇒{T_3}/{T_1}={p_3·V_3}/{p_1·V_1}⇒{T_3}/{T_1}={p_0·3V_0}/{3p_0·V_0}=1$.
Ответ: 1
Показать решение
Полный курс
Задача 16
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$_{He}=_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Ответ: 327
Показать решение
Полный курс
Задача 17
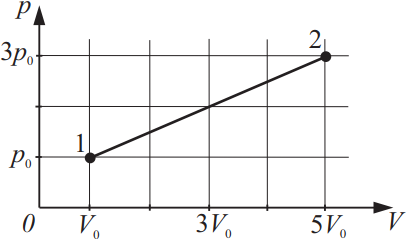
На рисунке изображено изменение состояния идеального газа. Во сколько раз температура в состоянии 2 больше, чем температура в состоянии 1?
Решение
Дано:
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
${T_2}/{T_1}-?$
Решение:
Из уравнения Менделеева-Клайперона: $pV={m}/{μ}RT$(1), следует равенство ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{p_0V_0}/{T_1}={3p_0·5V_0}/{T_2}$(2).
Из (2) имеем: $p_0V_0T_2=3p_0V_0·5T_1$
$T_2=3·5T_1⇒T_2=15T_1$ или ${T_2}/{T_1}=15$
Ответ: 15
Показать решение
Полный курс
Источник