Один и тот же сосуд поочередно заполняли при одинаковых условиях
1
Молярный объем газа – это объем, который занимает 1 моль газа
VM = V(газа) / n(газа); V(газа) = n(газа) ∙ VM; n(газа) = V(газа) / VM
н.у.: p = 101,3 кПа, Т = 0 оС = 273 К. VM (н.у.) = 22,4 л
Объединенный газовый закон: p1V1 / T1 = p2V2 / T2 = 101,3 ∙ V(н.у.) / 273
Уравнение Менделеева – Клапейрона: pV = nRT; R = 8,31 Дж/(моль∙К)
.2.1.Молярный объем газа (VM). Нормальные условия (н.у.).
Пример 17. Определите массу 26,88 л кислорода при нормальных условиях.
Решение:
Находим количество вещества: n(О2) = V(O2) / VM = 26,88 / 22,4 = 1,2 моль.
Определяем массу кислорода: m(O2) = n(О2) ∙ М(О2) = 1,2 ∙ 32 = 38,4 г.
Ответ: m(O2) = 38,4 г.
Пример 18. Масса 15 л газа при 18 оС и при давлении 122 кПа равна 30,3 г. Определите молярную массу этого газа.
Решение:
Переводим температуру в Кельвины: Т = 18 + 273 = 291 К.
Приводим объем к нормальным условиям, используя объединенный газовый закон:
V(н.у.) = (p ∙ V ∙ 273) / (T ∙ 101,3) = (122 ∙ 15 ∙ 273) / (291 ∙ 101,3) = 499590 / 29478,3 = 16,95 л.
Находим количество вещества и молярную массу газа:
n(газа) = V(н.у.) / VM = 16,95 / 22,4 = 0,757 моль; М(газа) = m(газа) / n(газа) = 30,3 / 0,757 = 40 г/моль.
Задачу можно также решить, используя уравнение Менделеева – Клапейрона:
n(газа) = pV / RT = (122 ∙ 15) / (8,31 ∙ 291) = 1830 / 2418 = 0,757 моль.
Ответ: М(газа) = 40 г/моль.
Пример 19. В сосуд емкостью 5,6 л поместили 75 г карбоната кальция. Сосуд закрыли и нагревали при 400 оС до полного разложения соли. Определите давление в сосуде при этой температуре.
Решение:
СаСО3 СаО + СО2
n(СО2) = n(СаСО3) = m(СаСО3) / М(СаСО3) = 75 / 100 = 0,75 моль.
Находим количество вещества воздуха, бывшего в сосуде:
n(воздуха) = V(сосуда) / 22,4 = 5,6 / 22,4 = 0,25 моль.
Находим общее количество вещества газов в сосуде после разложения:
n(газов) = n(воздуха) + n(СО2) = 0,75 + 0,25 = 1 моль.
Т = 400 + 273 = 673 К; p= nRT / V = (1 ∙ 8,31 ∙ 673) / 5,6 = 998,7 кПа.
Ответ: p = 998,7 кПа.
Задачи для самостоятельного решения.
Какой объем (н.у.) займет метан (СН4), масса которого равна массе 40 л азота (н.у.)
В результате прокаливания некоторого количества нитрата меди выделилось 11,2 л газов (н.у.). Определите массу исходной соли.
После прокаливания 66,6 г некоторого карбоната образовалось 48 г оксида металла (II), в котором массовая доля металла составляет 80 %, 6,72 л газа (н.у.) и некоторое количество воды. Определите формулу исходной соли.
Оксид углерода (IV), находившийся в баллоне емкостью 2,8 л под давлением 2000 кПа при температуре 25 оС, пропустили через избыток раствора гидроксида натрия. Определите массу образовавшейся соли.
1.2.2.Абсолютная () и относительная (d) плотность газа
= m / V [г/л]; m = ∙ V; M(газа) = ∙ VM; M(газа) = (н.у.) ∙ 22,4
D2 = 1 / 2 = M1 / M2; M1 = D2 M2
M(газа) = DH2∙ 2 = DN2∙ 28 = DO2∙ 32 = D(воздух) ∙ 29
Пример 20. Плотность газа при н.у. составляет 3,615 г/л. определите молярную массу газа и его плотность по водороду и по воздуху.
Решение:
Находим молярную массу газа: М(газа) = (н.у.) ∙ 22,4 = 3,615 ∙ 22,4 = 81 г/моль.
Находим плотность по водороду: DH2 = М(газа) / M(H2) = 81 / 2 = 40,5.
Находим плотность по воздуху: D(воздух) = М(газа) / М(воздуха) = 81 / 29 = 2,79.
Ответ: М(газа) = 81 г/моль; DH2 = 40,5; D(воздух) = 2,79.
Пример 21. Предложите возможные структурные формулы углеводорода, плотность которого по воздуху 1,448.
Решение:
Формула: СхНу. М(СхНу) = D(воздух) ∙ 29 = 1,448 ∙ 29 = 42 г/моль.
Углеводород с такой молярной массой не может содержать более трех атомов углерода, так как иначе его молярная масса было бы больше 42. Он также не может содержать меньше трех атомов углерода, так как иначе число атомов водорода было бы слишком велико.
у = 42 – 12 ∙ 3 = 6. Формула углеводорода С3Н6.
Такой формуле соответствуют два углеводорода – пропен (СН2=CH-CH3) и циклопропан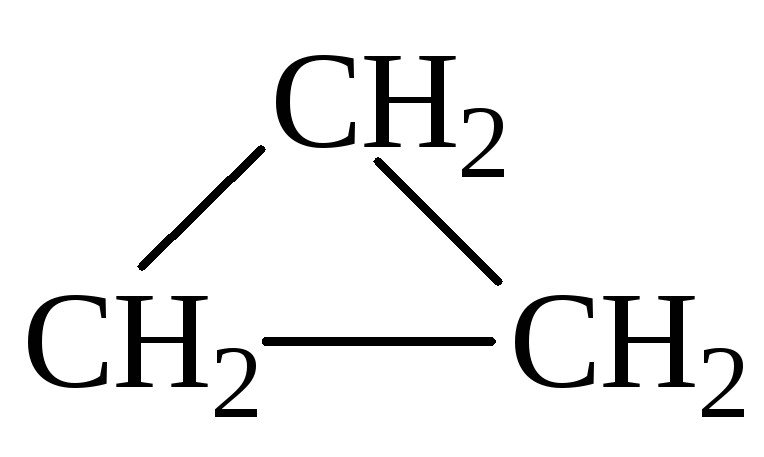
Ответ: пропен и циклопропан.
Пример 22. Один и тот же сосуд поочередно заполняли при одинаковых условиях тремя различными газами, причем масса заполненного сосуда каждый раз составляла 832, 942 и 858 г соответственно. Определите молярную массу первого газа, если известно, что плотность второго газа по третьему равна 2,45, а плотность третьего газа по водороду – 14,5.
Решение:
Находим молярные массы третьего и второго газа:
M(3) = DH2 ∙ M(H2) = 14,5 ∙ 2 = 29 г/моль;
М(2) = D3 ∙ М(3) = 2,45 ∙ 29 = 71 г/моль.
Поскольку объем газа во всех трех случаях был одинаковый, то и количества всех трех газов равны между собой. Пусть количество каждого газа равно х, а масса сосуда равна у, тогда масса третьего газа равна 29х,, а масса второго газа равна 71х.
Масса сосуда с газом во втором случае равна 71х + у, а в третьем случае 29х + у.
71х + у = 942 42х = 84 у = 942 – 71 ∙ 2 = 800 n(газа) = 2 моль;
29х + у = 858 х = 2 m(сосуда) = 800г.
m(первого газа) = 832 – 800 = 32 г; М(первого газа) = m(первого газа) / n(газа) = 32 / 2 = 16 г/моль.
Ответ: М(первого газа) = 16 г/моль.
Задачи для самостоятельного решения
Плотность газа по воздуху равна 1,586. Определите что это за газ, если известно, что он состоит из двух элементов, а массовая доля кислорода как элемента в нем составляет 69,5%.
Плотность паров фосфора при 400оС и при давлении 101,3 кПа равна 2,246 г/л. Определите молекулярную формулу фосфора в этих условиях.
Определите плотность газовой смеси по водороду, состоящей из 3 л азота и 7 л углекислого газа при нормальных условиях.
В каких объемных отношениях находятся в смеси кислород и метан (СН4), если относительная плотность этой смеси по водороду равна 10.
В каких объемных отношениях находятся в смеси азот и водород, если 10 л этой смеси при н.у. имеют массу 8 г.
В результате термического разложения 37,8 г неизвестной соли образовалось 3,36 л (н.у.) газообразного простого вещества с плотностью по водороду 14, 10,8 г оксида неметалла(I), в котором массовая доля кислорода составляет 88,89%, и оксид металла(III), в котором массовая доля металла составляет 68,42%. Определите простейшую формулу исходной соли.
1
=
; =
;
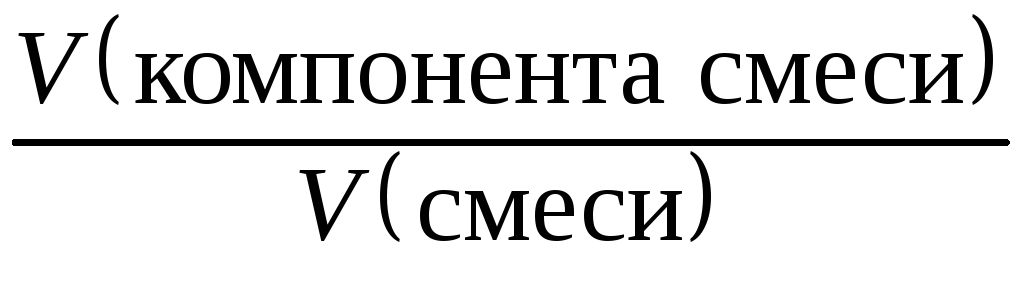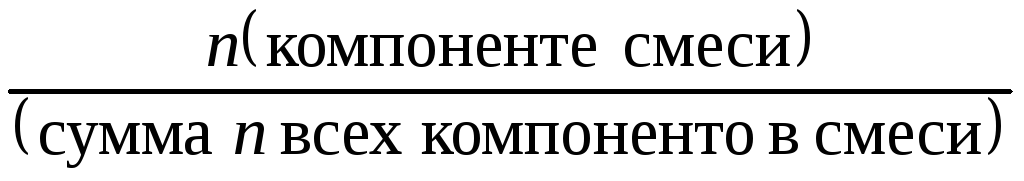% = ∙ 100; % = ∙ 100
Мср. = 1 ∙ М1 + 2 ∙ М2 + … по всем компонентам смеси. Для газов = .
Мср.(газа) = 1 ∙ М1 + 2 ∙ М2 +… по всем компонентам смеси.
Мср. =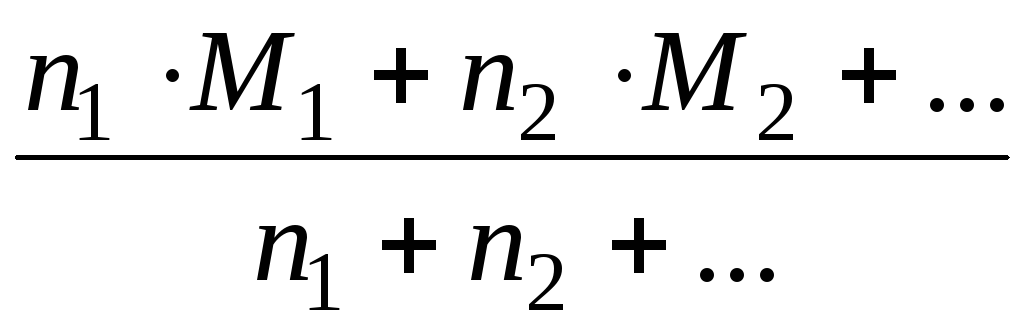
; Мср.(газа) =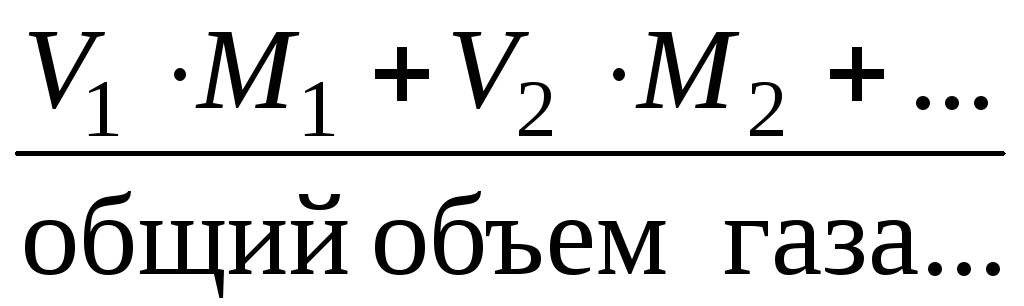 
.2.3. Объемная () и молярная () доля газа в смеси. Средняя молярная масса газовой смеси (Мср.)
Пример 23. Определите молярные и объемные доли метана и водорода в их смеси, если массовая доля метана в ней составляет 80 %.
Решение:
Пусть имеется 100 г смеси, тогда:
m(CH4) = 100 ∙ 0,8 = 80 г. m(Н2) = 100 – 80 = 20 г.
Определяем количества веществ газов:
n(СН4) = m(CH4) / М(CH4) = 80 / 16 = 5 моль;
n(Н2) = m(Н2) / М(Н2) = 20 / 2 = 10 моль. Сумма n всех компонентов смеси = 5 + 10 = 15 моль.
Определяем молярные и объемные доли газов:
(СН4) = (СН4) = n(СН4) / сумма n всех компонентов смеси = 5 / 15 = 0,333 (33,3%)
(Н2) = (Н2) = 1 – (СН4) = 1 – 0,333 = 0,667 (66,7%).
Ответ: (СН4) = (СН4) = 33,3%; (Н2) = (Н2) = 66,7%.
Пример 24. Определите среднюю молярную массу газа, полученного в результате термического разложения нитрата свинца(II).
Решение:
2Pb(NO3)2 2PbO + 4NO2 + O2
Газовая смесь состоит из NO2 и О2, причем согласно уравнению реакции из двух моль нитрата свинца образуются 4 моль оксида азота(IV) и 1 моль кислорода – всего 5 моль газов.
Рассчитываем молярные доли газов в этой смеси:
(NO2) = n(NO2) / [n(NO2) + n(O2)] = 4 / 5 = 0,8.
(O2) = n(O2) / [n(NO2) + n(O2)] = 1 / 5 = 0,2.
Определяем среднюю молярную массу газовой смеси:
Мср. = (NO2) ∙ М(NO2) + (O2) ∙ М(O2) = 0,8 ∙ 46 + 0,2 ∙ 32 = 43,2 г/моль.
Ответ: Мср. = 43,2 г/моль.
Пример 25. Какие объемы этана и водорода, измеренные при нормальных условиях, надо взять, чтобы приготовить 20 л (н.у.) газовой смеси с плотностью по воздуху 0,5.
Решение:
Определяем среднюю молярную массу газовой смеси:
Мср. = Dвоздух ∙ 29 = 0,5 ∙ 29 = 14,5 г/моль.
Рассчитываем исходные объемы газов, исходя из формулы для средней молярной массы:
14,5 = [V(С2Н6) ∙ 30 + V(Н2) ∙ 2] / 20; 30 ∙ V(С2Н6) + 2 ∙ V(Н2) = 14,5 ∙ 20 = 290.
30 ∙ V(С2Н6) + 2 ∙ V(Н2) = 290 30 ∙ V(С2Н6) + 2 ∙ V(Н2) = 290
V(С2Н6) + V(Н2) = 20 ∙2 2 ∙ V(С2Н6) + 2 ∙ V(Н2) = 40
28 ∙ V(С2Н6) = 250;
V(С2Н6) = 8,93 л; V(Н2) = 20 – V(С2Н6) = 20 – 8,93 = 11,07 л.
Ответ: V(С2Н6) = 8,93 л; V(Н2) = 11,07 л.
Пример 26. В сосуд емкостью 5,6 л, заполненный при нормальных условиях азотом, поместили 37 г смеси нитрата натрия и карбоната кальция. Сосуд закрыли и нагревали до полного разложения содержавшихся в нем солей. Определите массы веществ в твердом остатке после прокаливания и состав (в % по объему) газовой смеси, находящейся в сосуде после разложения солей, если известно, что ее плотность по кислороду равна 1,08.
Решение:
Рассчитываем количество вещества азота, находившегося в сосуде и среднюю молярную массу образовавшейся газовой смеси:
n(N2) = V(N2) / 22,4 = 5,6 / 22,4 = 0,25 моль.
Мср. = DO2 ∙ М(О2) = 1,08 ∙ 32 = 34,56 г/моль.
Пусть в исходной смеси было х моль нитрата натрия и у моль карбоната кальция.
Было: х
2NaNO3 2NaNO2 + O2
Образовалось: х 0,5х
Было: у
CaCO3 CaO + CO2
Образовалось: у у
m(NaNO3) = M(NaNO3) ∙ n(NaNO3) = 85x; m(CaCO3) = M(CaCO3) ∙ n(CaCO3) = 100y. 85x + 100y = 37.
n(газов в образовавшейся смеси) = n(N2) + n(O2) + n(CO2) = 0,25 + 0,5х + у.
Мср. = [0,25 ∙ 28 + 0,5х ∙ 32 + у ∙ 44] / 34,56 = 0,25 + 0,5х + у;
28 ∙ 0.25 + 32 ∙ 0,5x + 44 ∙ y = 34,56 ∙ (0,25 + 0,5х + у);
8,64 + 17,28х + 34,56у = 7 + 16х + 44у; 1,28х – 9,44у = – 1,64
Составляем систему уравнений и решаем ее:
85x + 100y = 37 85x + 100y = 37 727у = 145,9
1,28х – 9,44у = – 1,64 ∙ 85 / 1,28 85x – 627y = -108,9 у = 0,2
х = (37 – 20) / 85 = 0,2.
Находим объемные доли газов в смеси и массы образовавшихся твердых продуктов:
n(газов в образовавшейся смеси) = 0,25 + 0,5х + у = 0,25 + 0,1 + 0,2 = 0,55
(N2) = (N2) = 0,25 / 0,55 = 0,4545 (45,45%);
(O2) = (O2) = 0,1 / 0,55 = 0,1818 (18,18%);
(CO2) = (CO2) = 0,2 / 0,55 = 0,3636 (36,36%);
m(NaNO2) = M(NaNO2) ∙ x = 69 ∙ 0,2 = 13,8 г;
m(СаО) = M(СаО) ∙ у = 56 ∙ 0,2 = 11,2 г.
Ответ: (N2) = 45,45%; (O2) = 18,18%; (CO2) = 36,36%; m(NaNO2) = 13,8 г; m(СаО) = 11,2 г.
Задачи для самостоятельного решения
12,32 л смеси оксида азота(II) и оксида азота(IV) при н.у. имеют массу 19,86 г. Определите объемные доли газов в смеси.
К 20 л смеси метана и этилена добавили 10 л кислорода. Определите объемные доли веществ в полученной газовой смеси, если известно, что ее плотность по воздуху равна 0,8046.
Определите среднюю молярную массу газа, полученного в результате термического разложения нитрата серебра.
В результате термического разложения смеси нитратов серебра и меди образовалась газовая смесь с плотностью по воздуху 1,4655. Определите массовые доли веществ в исходной смеси солей.
Газовая смесь, образовавшаяся при прокаливании смеси карбоната кальция и нитрата меди, имеет плотность по водороду 21,75. Определите массовые доли веществ в остатке после прокаливания.
В результате термического разложения смеси нитратов калия и меди выделилось 8,4 л газа (н.у.). Определите массу исходной смеси солей, если известно, что в ней массовая доля азота как элемента составляла 14,302%.
В результате термического разложения 45 г нитрата неизвестного металла образовалось 20 г оксида металла(III), в котором массовая доля металла составляла 70%, и газовая смесь с плотностью 1,984 г/л (н.у.). Определите формулу исходной соли и запишите уравнение реакции ее разложения.
В результате сжигания 9,76 г органического вещества в избытке кислорода образовалось 10,08 г воды и 8,96 л (н.у.) смеси углекислого газа с азотом с плотностью по кислороду 1,275. Предложите структурную формулу сожженного вещества, если известно, что его молярная масса меньше 80 г/моль.
Соль органической кислоты сожгли в 9,8 л кислорода, при этом образовалось 7,29 г воды и 8,288 л смеси трех газов. После пропускания этой газовой смеси через избыток раствора щелочи ее объем уменьшился на 6,048 л, а оставшаяся азото-кислородная смесь имела плотность 1,3482 г/л. Определите формулу сожженного вещества. Все объемы измерены при нормальных условиях.
Образец аминокислоты, входящей в состав белков массой 4,68 г сожгли в избытке кислорода. После приведения продуктов сгорания к н.у. выделилось 3,96 г воды и осталось 5,376 л газовой смеси, объем которой уменьшился в 6 раз после пропускания через избыток раствора щелочи. Не поглощенная щелочью смесь газов имела плотность по водороду 15. Определите формулу сожженной аминокислоты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд – со вторым, второй – с третьим. Первоначально давление газа в сосудах было равно соответственно (р, 3р) и (р). В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
1) При первой открывании и закрывании кранов, в соответствии законам Дальтона и Бойля-Мариотта, установившееся давление во втором и третьем сосудах будет [dfrac{3p}{2}+dfrac{p}{2}=2p] 2) При втором открывании и закрывании, с учетом тех же законов, установившееся давление в первом и втором будет равно [dfrac{2p}{2}+dfrac{p}{2}=1,5p] 3) Так как объем сосуда не изменился, а температура по условию постоянна, то в соответствии закону Клайперона – Менделеева [pV=nu R T Rightarrow nu=dfrac{pV}{RT}] Знаменатель остался прежним, а числитель увеличился, значит и количество газа увеличилось.
Ответ:
Сжиженные газы с низкими температурами кипения хранят в открытых теплоизолированных резервуарах при нормальном давлении, с контактом с атмосферой. При таком хранении потери на испарение, отнесённые к единице массы сжиженного газа, уменьшаются при увеличении объёма сосуда. Объясните причины вышеизложенного, основываясь на известных физических законах и закономерностях.
1) Даже при хорошей теплоизоляции невозможно устранить полностью подвод тепла к сжиженным газам, значит, будет некоторое испарение вещества, потому что температура кипения таких газов ниже температуры атмосферы и существует теплопроводность.
2) Так как существует испарение, то в закрытых сосудах будет повышаться давление, что приведет к взрыву, поэтому газ хранят в открытых сосудах.
3) Подвод тепла к газу через стенки сосуда пропорционален площади стенок сосуда, а его масса пропорциональна объему. Объем же в свою очередь пропорционален кубу размеров сосуда. Поэтому с увеличением объема уменьшается испарение на единицу массы.
Ответ:
Чтобы вода в резервуаре быстрее закипела, источник тепла всегда помещают внизу. Желая охладить кастрюлю с горячей водой как можно быстрее, кастрюлю поставили на лёд. Является ли такой способ эффективным? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Нет, неверно.
Нагреватель ставится внизу, потому что нагретые слои воды, как более легкие, поднимаются вверх и таким образом достигается наиболее эффективное перемешивание и нагревание всей воды (по такому же принципу работает батарея в комнате). При охлаждении же дело происходит как раз наоборот: более холодные слои воды, как более тяжелые, опускаются вниз. Поэтому если поместить холодильник внизу, то перемешивания не будет, и остывание будет идти очень долго. Для более быстрого охлаждения надо поместить лед сверху.
Ответ:
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара (I) лежит выше изобары (II)? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.
1. Идеальный газ подчиняется закону Клапейрона-Менделеева: [pV=nu R T,] где (p) – давление газа, (V) – объем, (nu) – количество газа, (T) – температура газа в Кельвинах.
Выразим температуру [T=dfrac{pV}{nu R}] 2. Зафиксируем объем (V_0), при этом отношение температур равно [dfrac{T_I}{T_{II}}=dfrac{dfrac{pV_0}{nu_I R}}{dfrac{pV_0}{nu{II}R}}=dfrac{nu_{II}}{nu_{I}}>1] Значит количество газа во втором больше, чем количество газа в первом.
Ответ:
1 моль разреженного гелия участвует в циклическом процессе 1-2-3-4-1, график которого изображён на рисунке в координатах V-T, где V – объём газа, Т – абсолютная температура. Постройте график цикла в координатах p-V, где р – давление газа, V- объём газа. Опираясь на законы молекулярной физики и термодинамики, объясните построение графика. Определите, во сколько раз работа газа в процессе 2-3 больше модуля работы внешних сил в процессе 4-1.
Проанализируем процессы:
1-2: Процесс изохорный, по закону Шарля (dfrac{p}{T}=const), температура увеличилась в 3 раза, значит и давление увеличилось в 3 раза.
2-3: Процесс изобарный, по закону Гей-Люсака (dfrac{V}{T}=const) и объем и температура увеличились в 2 раза.
3-4: В процессе 3-4 газ изохорно уменьшил свою абсолютную температуру и давление в 3 раза.
4-1: Газ вернулся в первоначальное состояние Перестроим график цикла в координатах p-V (см. рисунок).
Работа газа в процессе 2-3 равна [A_{23}=pDelta V=3p_(2V_0-V_0)=3p_0V_0] Работа внешних сил в процессе 4-1 равна [|A_{41}|=pDelta V=p_0(2V_0-V_0)=p_0V_0] Значит работа газа в процессе 2-3 в 3 раза больше работы внешних сил в процессе 4-1.
Ответ:
На рисунке 1 приведена зависимость внутренней энергии (U) 2 моль идеального одноатомного газа от его давления p в процессе 1-2-3. Постройте график этого процесса на рисунке 2 в переменных (p-V). Точка, соответствующая состоянию 1, уже отмечена на этом рисунке. Построение объясните, опираясь на законы молекулярной физики.
1. Проанализируем процессы:
1-2: Внутренняя энергия прямо пропорциональна температуре газа (U=dfrac{3}{2}nu R T ), значит в процессе 1-2 температура увеличивается, давление тоже увеличивается (по графику ). По основному газовому закону (dfrac{pV}{T}=const) объем будет постоянен. График будет представлять собой вертикальную прямую
2-3: В процессе 2-3 внутренняя энергия газа постоянна, а значит и температура постоянна (по пункту 1), давление увеличивается, значит, по основному газовому закону объем будет уменьшаться. График будет представлять гиперболу.
2. Построим график
Ответ:
На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1-2 и 2-3.
1. Плотность находится по формуле: [rho=dfrac{m}{V} quad (1)] тогда уравнение Клайперона-Менделеева можно переписать в виде [pV=dfrac{m}{mu}RT Rightarrow p=dfrac{rho}{mu}RT, quad (2)] где (m) – масса газа, (V) – его объем, (T) – температура газа. 2. Процесс 1-2.
Плотность уменьшается при постоянном, в соответствии с формулой (1) объем будет увеличиваться, а температура будет увеличиваться в соответствии с формулой (2).
Процесс 2-3.
Плотность уменьшается вместе с давлением, причем давление уменьшается пропорционально плотности (p sim rho), а это означает, что температура газа постоянна, а по формуле (1) объем увеличивается.
Ответ:
Максим Олегович
????№16 из ЕГЭ 2014 по математике за 1 минуту. Стоит ли ботать №16 за 1,5 месяца до ЕГЭ?
‼️Премьера в 17:00‼️ Ставь напоминание Ссылка на видео????????
Математика: №16 из ЕГЭ 2014 по математике за 1 минуту!
Источник