Одинаковое ли давление на дно сосуда производят

Одинаковое ли давление на дно сосуда производят

Возьмем цилиндрический сосуд с горизонтальным дном и вертикальными стенками, наполненный жидкостью до высоты

(рис. 248).

Рис. 248. В сосуде с вертикальными стенками сила давления на дно равна весу всей налитой жидкости

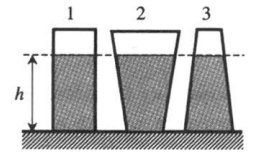
Рис. 249. Во всех изображенных сосудах сила давления на дно одинакова. В первых двух сосудах она больше веса налитой жидкости, в двух других – меньше

Гидростатическое давление в каждой точке дна сосуда будет одно и то же:

.

Если дно сосуда имеет площадь

, то сила давления жидкости на дно сосуда , т. е. равна весу жидкости, налитой в сосуд.

Рассмотрим теперь сосуды, отличающиеся по форме, но с одинаковой площадью дна (рис. 249). Если жидкость в каждом из них налита до одной и той же высоты

, то давление на дно . во всех сосудах одно и то же. Следовательно, сила давления на дно, равная

,

также одинакова во всех сосудах. Она равна весу столба жидкости с основанием, равным площади дна сосуда, и высотой, равной высоте налитой жидкости. На рис. 249 этот столб показан около каждого сосуда штриховыми линиями. Обратите внимание на то, что сила давления на дно не зависит от формы сосуда и может быть как больше, так и меньше веса налитой жидкости.

Рис. 250. Прибор Паскаля с набором сосудов. Сечения

одинаковы у всех сосудов

Рис. 251. Опыт с бочкой Паскаля

Этот вывод можно проверить на опыте при помощи прибора, предложенного Паскалем (рис. 250). На подставке можно закреплять сосуды различной формы, не имеющие дна. Вместо дна снизу к сосуду плотно прижимается подвешенная к коромыслу весов пластинка. При наличии жидкости в сосуде на пластинку действует сила давления, которая отрывает пластинку, когда сила давления начнет превосходить вес гири, стоящей на другой чашке весов.

У сосуда с вертикальными стенками (цилиндрический сосуд) дно открывается, когда вес налитой жидкости достигает веса гири. У сосудов другой формы дно открывается при той же самой высоте столба жидкости, хотя вес налитой воды может быть и больше (расширяющийся кверху сосуд), и меньше (суживающийся сосуд) веса гири.

Этот опыт приводит к мысли, что при надлежащей форме сосуда можно с помощью небольшого количества воды получить огромные силы давления на дно. Паскаль присоединил к плотно законопаченной бочке, налитой водой, длинную тонкую вертикальную трубку (рис. 251). Когда трубку заполняют водой, сила гидростатического давления на дно становится равной весу столба воды, площадь основания которого равна площади дна бочки, а высота равна высоте трубки. Соответственно увеличиваются и силы давления на стенки и верхнее днище бочки. Когда Паскаль заполнил трубку до высоты в несколько метров, для чего потребовалось лишь несколько кружек воды, возникшие силы давления разорвали бочку.

Как объяснить, что сила давления на дно сосуда может быть, в зависимости от формы сосуда, больше или меньше веса жидкости, содержащейся в сосуде? Ведь сила, действующая со стороны сосуда на жидкость, должна уравновешивать вес жидкости. Дело в том, что на жидкость в сосуде действует не только дно, но и стенки сосуда. В расширяющемся кверху сосуде силы, с которыми стенки действуют на жидкость, имеют составляющие, направленные вверх: таким образом, часть веса жидкости уравновешивается силами давления стенок и только часть должна быть уравновешена силами давления со стороны дна. Наоборот, в суживающемся кверху сосуде дно действует на жидкость вверх, а стенки – вниз; поэтому сила давления на дно оказывается больше веса жидкости. Сумма же сил, действующих на жидкость со стороны дна сосуда и его стенок, всегда равна весу жидкости. Рис. 252 наглядно показывает распределение сил, действующих со стороны стенок на жидкость в сосудах различной формы.

Рис. 252. Силы, действующие на жидкость со стороны стенок в сосудах различной формы

Рис. 253. При наливании воды в воронку цилиндр поднимается вверх.

В суживающемся кверху сосуде со стороны жидкости на стенки действует сила, направленная вверх. Если стенки такого сосуда сделать подвижными, то жидкость поднимет их. Такой опыт можно произвести на следующем приборе: поршень неподвижно закреплен, и на него надет цилиндр, переходящий в вертикальную трубку (рис. 253). Когда пространство над поршнем заполняется водой, силы давления на участках

и стенок цилиндра поднимают цилиндр вверх.

Источник

26. Закон Архимеда

Сборник задач по физике, Лукашик В.И.

606. К чашам весов подвешены два одинаковых железных шарика (рис. 183). Нарушится ли равновесие, если шарики опустить в жидкость? Ответ объясните.

Равновесие весов нарушится, так как архимедовы силы, действующие на шарики, будут различны. Перевесит чаша с шариком, погруженным в керосин, так как на нее будет действовать меньшая выталкивающая сила.

607. В сосуд погружены три железных шарика равных объемов (рис. 184). Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожной сжимаемости на любой глубине считать одинаковой.)

Выталкивающие силы, действующие на шарики, не зависят от глубины погружения и поэтому будут равны (рис. 184)

608. Свинцовая дробинка опускается с постоянной скоростью на дно сосуда, наполненного маслом. Какие силы действуют на дробинку?

На дробинку действуют сила тяжести, выталкивающая сила и сила вязкого трения. Эти силы скомпенсированы.

609. К чашам весов подвешены две гири равного веса: фарфоровая и железная. Нарушится ли равновесие весов, если гири опустить в сосуд с водой?

При одинаковом весе гирь объем железной гирьки будет меньше объема фарфоровой, так как плотность железа больше. Поэтому, если гири опустить в сосуд с водой, на фарфоровую будет действовать большая выталкивающая сила, и железная гиря перевесит.

610. В сосуде три жидкости: слегка подкрашенная вода, растворитель (четыреххлористый углерод) и керосин. Укажите на порядок расположения этих жидкостей. (Плотность растворителя 1595 кг/м3.)

Снизу вверх: четыреххлористый углерод, вода, керосин.

611. Почему горящий керосин нельзя тушить водой?

Потому что вода будет опускаться вниз и не будет закрывать доступ воздуха (необходимого для горения) к керосину.

612. На дне сосуда с водой лежат одинаковой массы шары: чугунный и железный. Одинаковое ли давление на дно сосуда производят эти шары?

Сила давления, оказываемая чугунным шаром, будет меньше, так как на него будет действовать большая выталкивающая сила, так как плотность чугуна меньше плотности железа. Если площади соприкосновения с дном одинаковы, то давление, оказываемое железным шаром, будет больше.

613. На поверхности воды плавают бруски из дерева, пробки и льда (рис. 185). Укажите, какой брусок пробковый, а какой из льда.

3 – брусок из пробки, 1 – брусок изо льда, так как плотность пробки наименьшая из заданных веществ, льда – наибольшая.

614. Березовый и пробковый шарики равного объема плавают на воде. Какой из них глубже погружен в воду? Почему?

Так как плотность березового шарика больше плотности пробкового, то он глубже будет погружен в воду.

615. Для отделения зерен ржи от ядовитых рожков спорыньи их смесь высыпают в воду. Зерна ржи и спорыньи в ней тонут. Затем в воду добавляют соль. Рожки начинают всплывать, а рожь остается на дне. Объясните это явление.

Объясняется это явление тем, что плотность рожков спорыньи меньше плотности соленой воды, а плотность ржи – больше.

616. В сосуд, содержащий воду, керосин и жидкий растворитель (четыреххлористый углерод, плотность которого равна 1595 кг/м3), опущены три шарика: парафиновый, пробковый и стеклянный. Как расположены шарики?

Пробковый шарик будет плавать на поверхности керосина, парафиновый – на границе вода – керосин, а стеклянный покоиться на дне сосуда.

617. В сосуде с водой (при комнатной температуре) плавает пробирка (рис. 186). Останется ли пробирка на такой же глубине, если воду слегка подогреть; охладить? (Увеличение объема пробирки при нагревании и охлаждении не учитывать. Охлаждение производить при температуре не ниже 4 °С.)

При нагревании воды пробирка начнет двигаться вниз, при охлаждении – вверх. Объясняется это тем, что плотность воды при нагревании уменьшается, а при охлаждении возрастает.

618. В сосуд с водой опущены три одинаковые пробирки с жидкостью (рис. 187). На какую из пробирок действует наибольшая выталкивающая сила? (Плотность воды на всей глубине считать одинаковой.) Ответ обоснуйте.

На вторую и третью пробирки действуют одинаковые по величине выталкивающие силы, равные весу вытесненной ими воды. На первую пробирку действует меньшая выталкивающая сила, так как вес вытесненной ей воды меньше, чем вес воды, вытесненной второй или третьей пробиркой.

619. На рисунке 188 изображен поплавок, который можно использовать как весы. Объясните, как действуют такие весы.

Поплавок будет погружаться в воду пропорционально нагружаемому весу. Поэтому его можно использовать как весы.

620. Пробирка, в которой находится брусок пластилина, плавает в воде (рис. 189, а). Изменится ли глубина погружения пробирки в воду, если пластилин вынуть и подклеить ко дну (рис. 189, 6)1 Если изменится, то как? Ответ объясните.

Глубина погружения пробирки не изменится, так как по-прежнему будет вытесняться количество воды, равное весу пробирки и пластилина. Если же пластилин отвалится и утонет, то глубина погружения пробирки уменьшится.

621. Стальной брусок подвешен к пружине и опущен в воду (рис. 190). С одинаковой ли силой давит вода на верхнюю и нижнюю поверхности бруска? Ответ обоснуйте.

Давление на нижнюю поверхность бруска будет больше, чем на верхнюю. Поэтому и сила давления на нижнюю поверхность бруска будет больше.

622. Подвешенный на нити стальной брусок погружен в воду (рис. 190). Назовите взаимодействующие тела и силы, действующие на брусок. Изобразите эти силы графически.

Брусок взаимодействует с Землей, пружиной и водой. Силы, действующие на брусок: сила тяжести, направленная вниз; сила Архимеда и сила упругости нити, направленные вверх. Сила тяжести равна по модулю сумме сил Архимеда и упругости нити.

623. Деревянный шар плавает на воде (рис. 191). Назовите силы, действующие на шар. Изобразите эти силы графически.

На шар действуют сила тяжести, направленная вниз, и сила Архимеда, направленная вниз. Сила тяжести равна по модулю силе Архимеда.

624. Стальной брусок, вес которого 15,6 Н, погрузили в воду (рис. 190). Определите значение и направление силы натяжения пружины.

625. Вычислите выталкивающую силу, действующую на гранитную глыбу, которая при полном погружении в воду вытесняет ее некоторую часть. Объем вытесненной воды равен 0,8 м3.

626. Железобетонная плита размером 3,5×1,5×0,2 м полностью погружена в воду. Вычислите архимедову силу, действующую на плиту.

627. Железобетонная плита размером 4×0,3×0,25 м погружена в воду на половину своего объема. Какова архимедова сила, действующая на нее?

628. Один брусок имеет размер 2x5x10 см, а соответствующий размер другого бруска в 10 раз больше (0,2×0,5×1 м). Вычислите, чему будут равны архимедовы силы, действующие на эти бруски при полном погружении их в пресную воду, в керосин.

629. Плавающий на воде деревянный брусок вытесняет воду объемом 0,72 м3, а будучи погруженным в воду целиком – 0,9 м3. Определите выталкивающие силы, действующие на брусок. Объясните, почему различны эти силы.

630. Определите показания пружинных весов при взвешивании в воде тел объемом 100 см3 из алюминия, железа, меди, свинца.

631. Определите, что покажут пружинные весы, если тела объемом 100 см3 из алюминия, железа, свинца взвешивать в керосине.

632. Чему равна архимедова сила, действующая в воде на тела объемом 125 см3 из стекла, пробки, алюминия, свинца?

633. Пробирку поместили в мензурку с водой. Уровень воды при этом повысился от деления 100 см3 до деления 120 см3. Сколько весит пробирка, плавающая в воде?

634. На сколько гранитный булыжник объемом 0,004 м3 будет легче в воде, чем в воздухе?

635. Какую силу надо приложить, чтобы поднять под водой камень массой 30 кг, объем которого 0,012 м3?

636. Брусок размером 20х 10×5 см может занимать в воде указанные на рисунке 192 положения. Докажите, что на него действует одна и та же выталкивающая сила.

Сила Архимеда равна весу жидкости, вытесненной телом, и не зависит от ориентации тела в жидкости.

637. До какого уровня поднимется вода в мензурке, если в ней будет плавать брусок; шар (рис. 193)?

638. Масса пробкового спасательного круга равна 4,8 кг. Определите подъемную силу этого круга в пресной воде.

639. Какой максимальной подъемной силой обладает плот, сделанный из 10 бревен объемом по 0,6 м3 каждое, если плотность дерева 700 кг/м3?

640. Плот состоит из 12 сухих еловых брусьев. Длина каждого бруса 4 м, ширина 30 см и толщина 25 см. Можно ли на этом плоту переправить через реку автомашину весом 10 кН?

641. Прямоугольная баржа длиной 5 м и шириной 3 м после загрузки осела на 50 см. Определите вес груза, принятого баржей.

642. Судно, погруженное в пресную воду до ватерлинии, вытесняет воду объемом 15 000 м3. Вес судна без груза равен 5 • 106 Н. Чему равен вес груза?

643. После разгрузки баржи ее осадка в реке уменьшилась на 60 см. Определите вес груза, снятого с баржи, если площадь сечения баржи на уровне воды равна 240 м2.

644. Площадь сечения теплохода на уровне воды равна 2000 м2. Сколько нужно добавить груза, чтобы теплоход погрузился в морской воде еще на 1,5 м, считая, что борта его на данном уровне вертикальны?

645. Сколько воды вытесняет плавающий деревянный брус длиной 3 м, шириной 30 см и высотой 20 см? (Плотность дерева 600 кг/м3.)

646. Площадь льдины 8 м2, толщина 25 см. Погрузится ли она целиком в пресную воду, если на нее встанет человек, вес которого равен 600 Н?

647. Какой минимальный объем должна иметь подводная часть надувной лодки массой 7 кг, чтобы удержать на воде юного рыболова, вес которого равен 380 Н?

648. Известно, что масса мраморной плиты равна 40,5 кг. Какую силу надо приложить, чтобы удержать эту плиту в воде?

649. Какую силу надо приложить, чтобы удержать под водой кусок пробкового дерева, масса которого равна 80 г?

650. Плавающее тело вытесняет керосин объемом 120 см3. Какой объем воды будет вытеснять это тело? Определите массу тела.

651. Используя данные рисунка 194, определите плотность камня.

652. Было установлено, что при полном погружении куска меди в керосин вес его уменьшается на 160 Н. Каков объем этого куска меди?

653. На коромысле весов уравновесили два одинаковых сосуда. Нарушится ли равновесие весов, если один сосуд поместить в открытую банку и заполнить ее углекислым газом (рис. 195)?

Равновесие весов нарушится, так как архимедова сила в случае углекислого газа больше, чем в воздухе. Поэтому правый сосуд перевесит.

654. Один из двух одинаковых воздушных шаров заполнили водородом, другой до такого же объема – гелием. Какой из этих шаров обладает большей подъемной силой? Почему?

Большей подъемной силой обладает шар, заполненный водородом, так как плотность водорода меньше плотности гелия.

655. Равны ли массы пятирублёвой монеты и куска пробки, уравновешенные на очень точных и чувствительных весах? Ответ объясните.

Массы пробки и монеты не равны из-за того, что на них действует различная сила Архимеда.

656. Назовите газы, в которых мог бы плавать мыльный пузырь, наполненный воздухом. (Весом пузыря пренебречь.)

Углекислый газ, озон, хлор, аргон, ксенон, криптон, находящиеся при давлении, равном атмосферному.

657. Детский шар объемом 0,003 м3 наполнен водородом. Масса шара с водородом 3,4 г. Какова подъемная сила детского шара?

658. Радиозонд объемом 10 м3 наполнен водородом. Какого веса радиоаппаратуру он может поднять в воздухе, если оболочка его весит 6 Н?

659. Масса снаряжения воздушного шара (оболочки, сетки, корзины) составляет 450 кг. Объем шара 1600 м3. Вычислите, какой подъемной силой будет обладать этот шар при наполнении его водородом, гелием, светильным газом. (Плотность светильного газа 0,4 кг/м3.)

660. Стратостат «СССР», на котором стратонавты поднялись на высоту 19 км, имел объем 24 500 м3. При подъеме в оболочке стратостата было только 3200 м3 водорода. Почему же объем оболочки сделали таким большим?

Объем оболочки стратостата был сделан с большим запасом, поскольку с высотой давление наружного воздуха падает.

Источник

Источник