Ортогональная проекция сосудов это

Проекция (лат. projectio – выбрасывание вперёд) – изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости.

Термин проекция также означает метод построения такого изображения и технические приёмы, в основе которых лежит этот метод.

Принцип

Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой О (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Соединив эти точки прямыми линиями в том же порядке, как они соединены в предмете, получим на плоскости перспективное изображение предмета или центральную проекцию.

Если центр проекции бесконечно удалён от картинной плоскости, то говорят о параллельной проекции, а если при этом проекционные лучи падают перпендикулярно к плоскости – то об ортогональной проекции.

Проекция широко применяется в инженерной графике, архитектуре, живописи и картографии.

Изучением проекций и методов проектирования занимается начертательная геометрия.

В оптике и технике

Проекция, проецирование в оптике и технике – процесс получения изображения на удалённом от оптического прибора экране методом геометрической проекции (кинопроектор, фотоувеличитель, диаскоп и т. п.) или (реже) синтезом изображения (лазерный проектор).

Предназначенный для этого прибор (если не имеет специального названия) называется проектор.

Не следует путать с осветительными приборами (прожектор), название которых происходит от того же латинского корня лат. projectio, предназначенными для освещения предметов, а не для переноса изображений. Хотя в отдельных случаях осветительные приборы могут участвовать в синтезе изображений, и потому эта грань несколько размыта.

Источники

• МЭСБЕ. Статья «Проекция»
• БСЭ. Статья «Проекция»
• Проекционный аппарат, Фотоувеличитель, Проекционное печатание, Кинопроекционный аппарат // Фотокинотехника: Энциклопедия / Главный редактор Е. А. Иофис. – М.: Советская энциклопедия, 1981.

Wiki Foundation. 2010.

Смотреть что такое “Ортогональная проекция” в других словарях:

• ортогональная проекция – Перспективная азимутальная картографическая проекция, получаемая при расположении точки зрения на бесконечно большом расстоянии от центра шара. → Рис. 233, с. 515 Syn.: ортографическая проекция … Словарь по географии

• ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ – (прямоугольная проекция) частный случай параллельной проекции, когда проектирующие лучи перпендикулярны оси проекций или плоскости проекций; используется в графических конструкторских и архитектурных работах … Большая политехническая энциклопедия

• ортогональная проекция – – [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN orthogonal projection … Справочник технического переводчика

• ортогональная проекция – stačiakampė projekcija usas T sritis fizika atitikmenys: angl. orthogonal projection; rectangular projection vok. rechteckige Projektion, f; rechtschnittige Projektion, f rus. ортогональная проекция, f; прямоугольная проекция, f pranc.… … Fizikos terminų žodynas

• Ортогональная проекция – частный случай параллельной проекции (См. Проекция), когда ось или плоскость проекций перпендикулярна (ортогональна) направлению проектирования … Большая советская энциклопедия

• ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ – см. Проекция … Большой энциклопедический политехнический словарь

• ПРОЕКЦИЯ – (от лат. projectio букв. бросание вперед), изображение пространственных фигур на плоскости (или на какой либо другой поверхности). Центральная проекция: из определенной точки О (центра проекции) через все точки данной фигуры проводятся лучи до… … Большой Энциклопедический словарь

• Проекция (геометрия) – У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия

• проекция – и; ж. [от лат. projectio бросание вперёд, вдаль] 1. Матем. Изображение пространственных фигур на плоскости. Картографические проекции. Горизонтальная, вертикальная п. П. пирамиды. Вычертить детали по трём проекциям. 2. Спец. Изображение на экране … Энциклопедический словарь

• ПРОЕКЦИЯ – (1) результат (см.) в виде (см.) на плоскости (поверхности) точки, линии, пространственного предмета и др. объектов; (2) один из способов получения в определённом масштабе изображения любого объёмного предмета (объекта) на плоскости.… … Большая политехническая энциклопедия

Источник

Ортогональная проекция (иногда называемая ортогональная проекция , раньше называлась аналеммой ) является средством представления трехмерных объектов в двух измерениях . Это форма параллельной проекции , в которой все линии проекции ортогональны плоскости проекции , в результате чего каждая плоскость сцены появляется в аффинное преобразование на поверхности просмотра. Лицевая сторона ортогональной проекции – это наклонная проекция , которая представляет собой параллельную проекцию, в которой линии проекции не ортогональны плоскости проекции.

Термин «ортогональный» иногда используется специально для изображений объектов, где главные оси или плоскости объекта также параллельны плоскости проекции, но они более известны как многовидовые проекции . Кроме того, когда главные плоскости или оси объекта в ортогональной проекции не параллельны плоскости проекции, а скорее наклонены, чтобы обнажить несколько сторон объекта, проекция называется аксонометрической проекцией . Подтипы многовидовой проекции включают планы, фасады и разрезы. Подтипы аксонометрической проекции включают изометрическую, диметрическую и триметрическую проекции.

Линза, обеспечивающая ортогональную проекцию, известна как телецентрическая линза в объектном пространстве .

Геометрия

Различные проекции и способы их создания

Простая орфографическая проекция на плоскость z = 0 можно определить следующей матрицей:

P = [1 0 0 0 1 0 0 0 0] { displaystyle P = { begin {bmatrix} 1 & 0 & 0 0 & 1 & 0 \ 0 & 0 & 0 \ end {bmatrix}}}

Для каждой точки v = (v x , v y , v z ) преобразованная точка Pv будет иметь вид

P v = [1 0 0 0 1 0 0 0 0] [vxvyvz] = [vxvy 0] { displaystyle Pv = { begin {bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 0 \ end {bmatrix}} { begin {bmatrix} v_ {x} \ v_ {y} \ v_ {z} end {bmatrix}} = { begin {bmatrix} v_ {x} \ v_ {y} \ 0 end {bmatrix}}}

Часто бывает более полезно использовать однородные координаты . Вышеупомянутое преобразование может быть представлено для однородных координат как

P = [1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1] { displaystyle P = { begin {bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 1 end {bmatrix}}}

Для каждого однородного вектора v = (v x , v y , v z , 1) преобразованный вектор Pv будет иметь вид

P v = [1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1] [vxvyvz 1] = [vxvy 0 1] { displaystyle Pv = { begin { bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 1 end {bmatrix}} { begin {bmatrix} v_ {x} \ v_ {y} \ v_ {z} \ 1 end {bmatrix}} = { begin {bmatrix} v_ {x} \ v_ {y} \ 0 \ 1 end {bmatrix}}}

В компьютерной графике одна из наиболее распространенных матриц, используемых для Ортогональная проекция может быть определена кортежем , (слева, справа, снизу, сверху, рядом, дальше), который определяет плоскости отсечения . Эти плоскости образуют коробку с минимальным углом в (левый, нижний, -ближе) и максимальным углом в (справа, вверху, -далее).

Коробка перемещается так, чтобы ее центр находился в начале координат, затем он масштабируется до единичного куба, который определяется наличием минимального угла в (−1, −1, −1) и максимального угла в (1,1,1).

Орфографическое преобразование может быть задано следующей матрицей:

P = [2 справа – слева 0 0 – справа + слева направо – слева 0 2 сверху – снизу 0 – сверху + снизу сверху – снизу 0 0 – 2 далеко – близко – далеко + ближний – близко 0 0 0 1] { displaystyle P = { begin {bmatrix} { frac {2} {right-left}} & 0 & 0 & – { frac {right + left} {right -left}} \ 0 & { frac {2} {top-}} & 0 & – { frac {top + } {top-}} \ 0 & 0 & { frac {-2} {далеко-близко} } & – { frac {far + near} {far-near}} \ 0 & 0 & 0 & 1 end {bmatrix}}}

, который может быть задан как масштабирование S, за которым следует перевод T формы

P = ST = [2 справа – слева 0 0 0 0 2 сверху – снизу 0 0 0 0 2 далеко – около 0 0 0 0 1] [1 0 0 – слева + справа 2 0 1 0 – верх + низ 2 0 0 – 1 – далеко + около 2 0 0 0 1] { displaystyle P = ST = { begin {bmatrix} { frac {2} {right-left}} & 0 & 0 & 0 0 & { frac {2} {top-}} & 0 & 0 \ 0 & 0 & { frac {2} {far-near}} & 0 \ 0 & 0 & 0 & 1 end {bmatrix}} { begin {bmatrix} 1 & 0 & 0 & – { frac {left + right} {2}} \ 0 & 1 & 0 & – { frac {top + } {2}} \ 0 & 0 & -1 & – { frac {far + near} {2}} \ 0 & 0 & 0 & 1 end {bmatrix}}}

Определяется инверсия матрицы проекции P, которая может использоваться в качестве матрицы непроекции:

P – 1 = [right – left 2 0 0 left + right 2 0 top – нижний 2 0 верхний + нижний 2 0 0 далеко – рядом – 2 – далеко + рядом 2 0 0 0 1] { displaystyle P ^ {- 1} = { begin {bmatrix} { frac {right-left} {2 }} & 0 & 0 & { frac {left + right} {2}} \ 0 & { frac {top-} {2}} & 0 & { frac {top + } {2}} \ 0 & 0 & { frac { far-near} {- 2}} & – { frac {far + near} {2}} \ 0 & 0 & 0 & 1 end {bmatrix}}}

Подтипы

Символы, используемые для определения того, будет ли многовидовая проекция является либо третьим углом (справа), либо первым углом (слева).

Классификация ортогональной проекции и некоторых трехмерных проекций

В многоракурсных проекциях создается до шести изображений объекта, причем каждая плоскость проекции параллельна к одной из координатных осей объекта. Виды располагаются относительно друг друга по одной из двух схем: проекция под первым углом или проекция под третьим углом. В каждом из них видимость видов может рассматриваться как проекция на плоскости, которые образуют шестигранную рамку вокруг объекта. Хотя можно нарисовать шесть разных сторон, обычно три вида чертежа дают достаточно информации, чтобы создать трехмерный объект. Эти виды известны как вид спереди, вид сверху и вид с торца. Другие названия этих видов включают план, отметку и разрез.

Термин аксонометрическая проекция (не путать со связанным принципом аксонометрии , как описано в теореме Польке ) используется для описания типа ортогональной проекции, где плоскость или ось изображенного объекта не параллельна плоскости проекции, и на одном изображении видны несколько сторон объекта. Далее она подразделяется на три группы: изометрические, диметрические и триметрические проекции, в зависимости от точного угла, под которым вид отклоняется от ортогонального. Типичной характеристикой аксонометрической проекции (и других изображений) является то, что одна ось пространства обычно отображается как вертикальная.

Картография

Ортографическая проекция (экваториальный аспект) восточного полушария 30 ° з.д. – 150 ° в.д.

Орфографическая проекционная карта – это картографическая проекция из картографии . Подобно стереографической проекции и гномонической проекции , ортогональная проекция – это перспективная (или азимутальная) проекция , в которой сфера проецируется на касательная плоскость или секущая плоскость . Точка перспективы для ортогональной проекции находится на бесконечном расстоянии. На нем изображено полушарие земного шара , как оно появляется из космического пространства , где горизонт представляет собой большой круг . Формы и области искажены , особенно около краев.

Орфографическая проекция известна с древних времен, и ее картографическое использование хорошо задокументировано. Гиппарх использовал проекцию во 2 веке до нашей эры, чтобы определить места восхода и захода звезд. Примерно в 14 г. до н.э. римский инженер Марк Витрувий Поллион использовал проекцию для построения солнечных часов и для вычисления положения солнца.

Витрувий, похоже, также придумал термин орфографический (от греческого orthos (= «Прямой») и graphē (= «рисунок») для проекции. Однако название аналемма , которое также означало солнечные часы, показывающие широту и долготу, было общим названием до François d’Aguilon Антверпена получил свое нынешнее название в 1613 году.

Самые ранние сохранившиеся карты на проекции представлены в виде гравюр на дереве земных глобусов 1509 года (анонимно), 1533 и 1551 годов (Иоганнес Шенер), а также 1524 и 1551 годов. (Апианский).

Примечания

Ссылки

Внешние ссылки

• Нормальный (ортогональный) Аксонометрия (на немецком языке)
• Ортографическая проекция, видео и математика

(Wayback Machine копия)

Источник

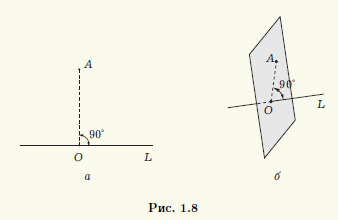
Пусть на плоскости заданы прямая L и точка A. Опустим из точки A на прямую L перпендикуляр (рис. 1.8, а). Тогда его основание (точку O) называют ортогональной проекцией точки A на прямую L. Если прямая L и точка A заданы в пространстве, то в этом случае ортогональной проекцией точки A на прямую L называют точку O пересечения прямой L с перпендикулярной ей плоскостью, проходящей через точку A (рис. 1.8, б). Если точка A лежит на прямой L, то она совпадает со своей ортогональной проекцией на L.

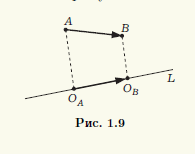
Для вектора – AB (на плоскости или в пространстве) можно построить ортогональные проекции на прямую L его начала и конца (рис. 1.9). Вектор OAOB, соединяющий эти проекции OA и OB и лежащий на прямой L, называют ортогональной проекцией вектора AB на прямую L.

Прямую, на которой задано одно из двух возможных направлений, называют осью. Выбранное направление на оси изображают с помощью стрелки на соответствующем конце оси. Ортогональную проекцию OAOB вектора AB на ось l можно полностью описать длиной вектора OAOB, приписав ей знак,

указывающий направление вектора. Если направление OAOB совпадает с заданным направлением оси, то берут знак плюс, а если направление вектора противоположно направлению оси, то берут знак минус. Длину вектора OAOB со знаком, определяющим направление этого вектора, называют ортогональной проекцией вектора AB на ось l и обозначают прlа.

Обратим внимание на то, что ортогональной проекцией вектора на ось является число, в то время как ортогональная проекция вектора на прямую – это вектор. Чтобы вектору соответствовало число как его проекция, на прямой нужно выбрать одно из двух возможных направлений.

Каждый ненулевой вектор l однозначно определяет ось: его можно рассматривать расположенным на некоторой прямой и задающим на ней направление. Ортогональную проекцию вектора на такую ось называют ортогональной проекцией этого вектора на направление вектора l.

Угол между направлениями двух ненулевых векторов называют углом между этими векторами. Угол может изменяться в пределах от 0 до π. Крайние значения 0 и π отвечают коллинеарным векторам, соответственно однонаправленным и противоположно направленным. Если хотя бы один из двух векторов является нулевым, то угол между такими векторами не определен. Удобно, однако, считать, что в этом случае угол имеет произвольное значение. Так, нулевой вектор коллинеарен любому другому, что формально соответствует углу 0 (или π). Конкретное значение, приписываемое углу между нулевым вектором и каким-либо другим, выбирают исходя из ситуации.

Теорема 1.1. Ортогональная проекция вектора а на направление ненулевого вектора l равна длине |а|, умноженной на косинус угла φ между векторами а и l, т.е.

прl = а|а| cos

где – угол между векторами а и l

◄ Пусть вектор l лежит на прямой L, а его началом является точка A. Совместим начало вектора а с точкой A, и пусть его концом будет точка B (рис. 1.10). Построим ортогональную проекцию C точки B на прямую L. Тогда вектор AC является ортогональной проекцией вектора а = AB на прямую L.

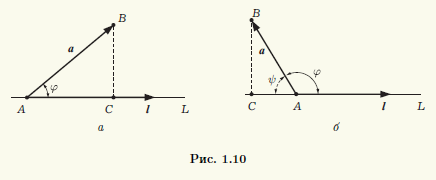
Если угол φ между векторами а и l острый (как это показано на рис. 1.10, а), то конец вектора l и точка C лежат по одну сторону от точки A. В этом случае проекция а на направление вектора l равна длине |AC| = |AB| cosφ катета AC треугольника ABC.

Если угол φ тупой (см. рис. 1.10, б), то конец вектора l и точка C лежат по разные стороны от точки A. Это значит, что векторы AC и l имеют противоположные направления, а проекция вектора а равна – |AC|. В треугольнике ABC угол ψ, прилежащий к катету AC, равен π – φ, поэтому |AC| = |AB| cos( π – φ) = – |AB| cosφ.

Если же φ = π/2 или а = 0, то точка C совпадает с точкой A и вектор AC является нулевым вектором. Однако cosπ/2 = 0, следовательно, и в этом случае утверждение теоремы справедливо. ►

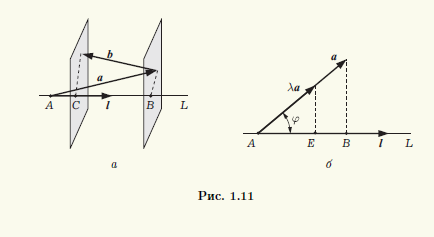
Теорема 1.2. Ортогональная проекция суммы векторов на направление ненулевого вектора равна сумме их ортогональных проекций на направление этого вектора, а при умножении вектора на число его ортогональная проекция на направление ненулевого вектора умножается на то же число:

прl(а + b) = прlа + прlb, прl(λа) – λпрlа.

◄ Доказательство следует из рис. 1.11. В случае, изображенном на рис. 1.11, а, имеем прlа = |AB|, прlb = -|BC|, прl(а + b) = |AC| = |AB| – |BC|. В случае, изображенном на рис. 1.11, б, прlа = |AB| и, если λ > 0, прl(λа) = |AE| = λ|AB|. Остальные варианты (точка C не принадлежит отрезку AB в случае а, λ ≤ 0 в случае б) рассматриваются аналогично. ►

Источник