От чего зависит плотность газа в сосуде

Введение

Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].

Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.

Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.

К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.

В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.

Математическая модель определения плотности газа

Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:

1. Уравнение Менделеева-Клапейрона:

(1),

где:

– давление газа;

– молярный объём;

R – универсальная газовая постоянная,

;

T – абсолютная температура, T=273.16 К.

2. Два измеряемых параметра:

p – давление газа, Па

t – температура газа, °С.

Известно, что молярный объём зависит от объёма газа V и количества молей газа в этом объёме:

(2)

Также известно, что

(3),

где: m – масса газа, M – молярная масса газа.

Учитывая (2) и (3) перепишем (1) в виде:

(4).

Как известно, плотность вещества

равна:

(5).

Из (4) и (5) выведем уравнение для плотности газа

:

(6)

и введём обозначение параметра

, который зависит от молярной массы газовой смеси:

(7).

Если состав газовой смеси не меняется, то параметр k является константой.

Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.

Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.

Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:

Молярные массы этих веществ воздуха будут соответственно равны:

, г/моль.

Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:

Теперь, зная значение константы

, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений

и t:

Приведение плотности газа к нормальным, стандартным условиям

Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].

Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.

Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.

Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.

Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура и абсолютное давление :

(9).

Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для :

(10).

Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура и абсолютное давление

:

(11).

В уравнениях (10) и (11) используем значения параметров воздуха , T и P из уравнения (8), полученные в рабочих условиях.

Реализация измерительного канала давления и температуры

Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.

Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).

Для этого, на аппаратном уровне, нам понадобятся компоненты:

1. Arduino (Uno, …) – используем как программатор;
2. микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
3. кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
4. тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
5. BMP180 – измерительный преобразователь температуры и давления с интерфейсом I2C;
6. преобразователь интерфейсов TTL/USB;
7. расходные материалы – провода, припой, монтажная плата, и др.

Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.

Рис. 1 – Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры

Теперь рассмотрим этапы осуществления нашей задачи.

1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.

2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.

Рис. 2 – Схема подключения микроконтроллера к программатору

3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры

Листинг 1 – Программа опроса измерительного преобразователя давления и температуры

#include <SFE_BMP180.h> SFE_BMP180 pressure; double T,P; void setup() { Serial.begin(9600); pressure.begin(); } void loop() { P = getPressure(); Serial.ln(P+0.5, 2); Serial.ln(T+0.54, 2); delay(1000); } double getPressure(){ char us; us = pressure.startTemperature(); if (us != 0){ delay(us); // ожидание замера температуры us = pressure.getTemperature(T); if (us != 0){ us = pressure.startPressure(3); if (us != 0){ delay(us); // ожидание замера давления us = pressure.getPressure(P,T); if (us != 0){ return(P); } } } } }

Программа Python для фильтрации по каналам температуры и давления, и получение результатов

Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.

Листинг 2 – Определение плотности газа по результатам измерения давления и температуры

import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import , from pykalman import KalmanFilter #вводим матрицу перехода и матрицу наблюдений transition_matrix = [[1, 1, 0, 0], [0, 1, 0, 0], [0, 0, 1, 1], [0, 0, 0, 1]] observation_matrix = [[1, 0, 0, 0], [0, 0, 1, 0]] #вводим и инициируем матрицу измерений initial_e_mean = [101000, 0, 28, 0] #параметры уравнения состояния идеального газа: #универсальная газовая постоянная R, [Дж/(моль*К)] R = 8.314459848 #молярная масса воздуха M, [г/моль] M = 29.04 #коэффициент k = M/R, [г/(Дж*К)] k = M / R #абсолютная температура, [K] K = 273.16 #стандартное (нормальное) давление, [Па] Pn = 101325 #определяем количество измерений # общее количество измерений str_m = input(“введите количество измерений: “) m = eval(str_m) # количество элементов выборки mw = 16 #настроить параметры последовательного порта ser = serial.Serial() ser.baudrate = 9600 port_num = input(“введите номер последовательного порта: “) ser.port = ‘COM’ + port_num ser #открыть последовательный порт try: ser.open() ser.is_open (“соединились с: ” + ser.portstr) except serial.SerialException: (“нет соединения с портом: ” + ser.portstr) raise SystemExit(1) #определяем списки l1 = [] # для значений 1-го параметра l2 = [] # для значений 2-го параметра t1 = [] # для моментов времени lw1 = [] # для значений выборки 1-го параметра lw2 = [] # для значений выборки 2-го параметра n = [] # для значений моментов времени nw = [] # для значений выборки моментов времени l1K = [] # для фильтрованных значений 1-го параметра l2K = [] # для фильтрованных значений 2-го параметра ro = [] # для плотности газовой среды #подготовить файлы на диске для записи filename = ‘count.txt’ in_file = open(filename,”r”) count = in_file.read() count_v = eval(count) + 1 in_file.close() in_file = open(filename,”w”) count = str(count_v) in_file.write(count) in_file.close() filename = count + ‘_’ + filename out_file = open(filename,”w”) #вывод информации для оператора на консоль (“nпараметры:n”) (“n – момент времени, с;”) (“P – давление, Па;”) (“Pf – отфильтрованное значение P, Па;”) (“T – температура, град. С;”) (“Tf – отфильтрованное значение T, град. С;”) (“ro – плотность воздуха, г/м^3;”) (“nизмеряемые значения величин параметровn”) (‘{0}{1}{2}{3}{4}{5}n’.format(‘n’.rjust(3),’P’.rjust(10),’Pf’.rjust(10), ‘T’.rjust(10),’Tf’.rjust(10),’ro’.rjust(10))) #считываение данных из последовательного порта #накопление списков #формирование текущей выборки i = 0 while i < m: n.append(i) nw.append(n[i]) if i >= mw: nw.pop(0) ser.flushInput() #flush input buffer, discarding all its contents line1 = ser.readline().decode(‘utf-8’)[:-1] line2 = ser.readline().decode(‘utf-8’)[:-1] t1.append(.()) if line1: l = eval(line1) #l = np.random.normal(l,100.0) l1.append(l) lw1.append(l1[i]) if i >= mw: lw1.pop(0) if line2: l = eval(line2) #l = np.random.normal(l,1.5) l2.append(l) lw2.append(l2[i]) if i >= mw: lw2.pop(0) #————————- initial_e_mean = [l1[i],0,l2[i],0] kf1 = KalmanFilter(transition_matrices = transition_matrix, observation_matrices = observation_matrix, initial_e_mean = initial_e_mean) if i == 0: measurements = np.array( [ [l1[i], l2[i]], [initial_e_mean[0], initial_e_mean[2]] ] ) measurements = np.array( [ [l1[i], l2[i]], [l1[i-1], l2[i-1]] ] ) kf1 = kf1.em(measurements, n_iter=2) (smoothed_e_means, smoothed_e_covariances) = kf1.smooth(measurements) l1K.append(smoothed_e_means[0, 0]) l2K.append(smoothed_e_means[0, 2]) #плотность воздуха в рабочих условиях #ro.append( k * l1K[i]/( l2K[i] + K) ) #плотность воздуха, приведенная к стандартным условиям ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/K/l1K[i]) ) #плотность воздуха, приведенная к нормальным условиям #ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/(K+20)/l1K[i]) ) (‘{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}’. format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i])) i += 1 ser.close() _tm = t1[m – 1] – t1[0] (“nпродолжительность времени измерений: {0:.3f}, c”.format(_tm)) Ts = _tm / (m – 1) (“nпериод опроса датчика: {0:.6f}, c”.format(Ts)) #запись таблицы в файл (“nтаблица находится в файле {}n”.format(filename)) for i in np.arange(0,len(n),1): out_file.write(‘{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}n’. format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i])) #закрыть файл с таблицей out_file.close() now = ..now() #получаем дату и время #выводим графики plt.figure(‘давление’) plt.plot( n, l1, “b-“, n, l1K, “r-“) plt.ylabel(r’$давление, Па$’) plt.xlabel(r’$номер измерения$’ + ‘; (период опроса датчика: {:.6f}, c)’.format(Ts)) plt.title(“BMP180n(” + now.strf(“%d-%m-%Y %H:%M”) + “)”) plt.grid(True) plt.figure(‘температура’) plt.plot( n, l2, “b-“, n, l2K, “r-“) plt.ylabel(r’$температура, degree С$’) plt.xlabel(r’$номер измерения$’ + ‘; (период опроса датчика: {:.6f}, c)’.format(Ts)) plt.title(“BMP180n(” + now.strf(“%d-%m-%Y %H:%M”) + “)”) plt.grid(True) plt.figure(‘плотность воздуха’) plt.plot( n, ro, “r-“) plt.ylabel(r’$плотность воздуха, г/м^3$’) plt.xlabel(r’$номер измерения$’ + ‘; (период опроса датчика: {:.6f}, c)’.format(Ts)) plt.title(“BMP180n(” + now.strf(“%d-%m-%Y %H:%M”) + “)”) plt.grid(True) plt.show()

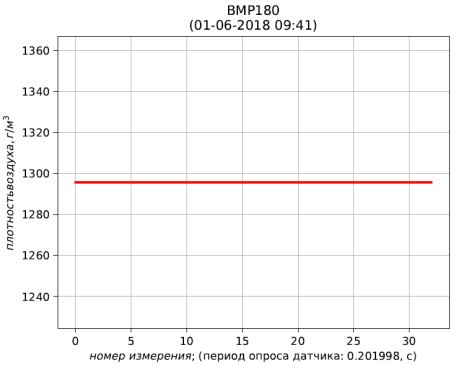
Результаты расчёта представлены листингом и рис. 4, 5, 6.

Интерфейс пользователя и таблица результатов расчёта

введите количество измерений: 33 введите номер последовательного порта: 6 соединились с: COM6 параметры: n – момент времени, с; P – давление, Па; Pf – отфильтрованное значение P, Па; T – температура, град. С; Tf – отфильтрованное значение T, град. С; ro – плотность воздуха, г/м^3; измеряемые значения величин параметров n P Pf T Tf ro 0 101141.000 101141.000 28.120 28.120 1295.574 1 101140.000 101140.099 28.190 28.183 1295.574 2 101140.000 101140.000 28.130 28.136 1295.574 3 101141.000 101140.901 28.100 28.103 1295.574 4 101140.000 101140.099 28.100 28.100 1295.574 5 101141.000 101140.901 28.110 28.109 1295.574 6 101141.000 101141.000 28.100 28.101 1295.574 7 101139.000 101139.217 28.100 28.100 1295.574 8 101138.000 101138.099 28.090 28.091 1295.574 9 101137.000 101137.099 28.100 28.099 1295.574 10 101151.000 101149.028 28.100 28.100 1295.574 11 101136.000 101138.117 28.110 28.109 1295.574 12 101143.000 101142.052 28.110 28.110 1295.574 13 101139.000 101139.500 28.100 28.101 1295.574 14 101150.000 101148.463 28.110 28.109 1295.574 15 101154.000 101153.500 28.120 28.119 1295.574 16 101151.000 101151.354 28.110 28.111 1295.574 17 101141.000 101142.391 28.130 28.127 1295.574 18 101141.000 101141.000 28.120 28.121 1295.574 19 101142.000 101141.901 28.110 28.111 1295.574 20 101141.000 101141.099 28.120 28.119 1295.574 21 101142.000 101141.901 28.110 28.111 1295.574 22 101146.000 101145.500 28.120 28.119 1295.574 23 101144.000 101144.217 28.130 28.129 1295.574 24 101142.000 101142.217 28.130 28.130 1295.574 25 101142.000 101142.000 28.140 28.139 1295.574 26 101142.000 101142.000 28.130 28.131 1295.574 27 101146.000 101145.500 28.150 28.147 1295.574 28 101142.000 101142.500 28.190 28.185 1295.574 29 101146.000 101145.500 28.230 28.225 1295.574 30 101146.000 101146.000 28.230 28.230 1295.574 31 101146.000 101146.000 28.220 28.221 1295.574 32 101150.000 101149.500 28.210 28.211 1295.574 продолжительность времени измерений: 6.464, c период опроса датчика: 0.201998, c таблица находится в файле 68_count.txt

Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления

Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры

Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)

Выводы

Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.

Ссылки на источники информации

1. ГОСТ 8.586.5-2005. URL
2. ГОСТ Р 8.740 – 2011. URL
3. Ideal gas law. URL
4. Standard conditions for temperature and pressure. URL

Источник