От нее зависит давление жидкости на дно и стенки сосуда
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2020; проверки требуют 7 правок.
Гидростатическое давление – давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w, то есть давление р на поверхность, равную единице, называется гидростатическим давлением[1].
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].
Вычисление[править | править код]
В каждой жидкости существует давление, обусловленное её собственным весом ; так как , то ; учтём, что и получим формулу .
Плотность жидкости зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением[2].
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).
История открытия[править | править код]
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 г., хотя несколько ранее оно было уже известно Стевину[источник не указан 1276 дней].
Единица измерения[править | править код]
Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.
Свойства[править | править код]
Гидростатический парадокс[править | править код]
Гидростатическое давление на тело не зависит от направления.
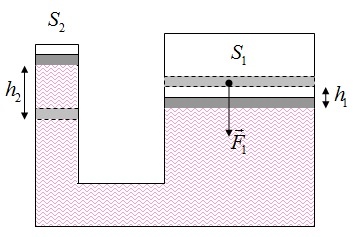
Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
Закон Паскаля[править | править код]
Чем глубже, тем выше давление. (левая часть графика)
Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести ( = несжимаемая жидкость) подчиняется закону Паскаля:
где:
– плотность [для пресной воды: ρ ≈ 1000 кг/м³] – ускорение свободного падения [для Европы: g ≈ 9,81 м/с²] – высота (здесь: жидкости) [м] – [Па]
⇒ = гидростатическое давление (p) зависит от высоты (h) жидкости.[4]
Примечания[править | править код]
Литература[править | править код]
- В. В. Лермантов. Гидростатическое давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1893. – Т. VIIIa. – С. 655-656.
Источник
Что такое давление жидкости
Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.
Теорема
Давление – физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.
На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости – ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества – например, температурой Т и плотностью (rho.)
Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:
(rho = const.)
Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:
(р = р_{0} + rhos gs h.)
(rho) здесь – плотность вещества, (р_{0}) – атмосферное давление, g – ускорение свободного падения, h – глубина погружения.
История открытия
Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.
Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.
Определение
В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.
Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.
Факторы, влияющие на показатель
На давление жидкости могут влиять:
- ее плотность;
- атмосферное давление;
- температура;
- глубина сосуда;
- площадь дна сосуда.
Давление на дно и стенку сосуда
Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.
Расчет давления жидкости на дно и стенки сосуда
Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.
В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.
Единицы измерения
В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.
Определение
Атмосфера – внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.
Формулы расчета
Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:
(р = frac{F}{S}.)
F – сила, с которой происходит воздействие на поверхности сосуда, S – площадь этой поверхности.
В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:
(р = rhos gs h.)
Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.
(m = rhos V = rhos Ss h)
Вес (Р = g s m = gs rhos Ss h.)
Вес столба, давящего на дно сосуда, равен силе, и тогда:
(р = frac{Р}{S} = gs rhos Ss frac{h}{S} = gs rhos h.)
Применение на практике
Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.
Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:
(frac{F_{2}h_{2}}{F_{1}h_{1}})
Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене – это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.
Гидростатический парадокс
Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.
Источник
«Я ИДУ НА УРОК»
Н.В.ЩЕРБАКОВА,
МОУ, гимназия № 72, г. Прокопьевск
Урок объяснения нового материала. 7-й класс
Цели урока: обнаружить наличие давления жидкости на дно и стенки сосуда, установить, от каких факторов оно зависит, и вывести формулу для его расчёта р = gh.
Образовательные задачи: дать учащимся представление о том, что жидкость давит на дно и стенки сосуда; раскрыть причину возникновения этого давления; определить, от чего зависит давление жидкости на дно сосуда; вывести формулу расчёта давления жидкости на дно сосуда р = gh.
Развивающие задачи: продолжить формирование умений проводить эксперимент, планировать свои действия, оформлять результаты; развивать интерес и логическое мышление путём решения проблем.
Воспитательные задачи: продолжить расширять кругозор учащихся; формировать бережное отношение к физическому оборудованию; воспитывать аккуратность, умение вести записи в тетрадях, наблюдать, исследовать, замечать закономерности явлений, аргументировать свои выводы.
План урока
Ход урока
1. Проблемный опыт. Учитель берёт цилиндрический сосуд, дно которого заменяет резиновая плёнка, и наливает в него воду.
Учебная проблема. Почему у сосуда прогнулось дно? (Учащиеся: вода давит на дно сосуда.)
Учитель предлагает выяснить, почему возникает это давление.
2. Работа в группах (по 5-6 человек). Предлагается объяснить, как возникает давление жидкости на дно сосуда. Учитель, переходя от группы к группе, помогает учащимся, задавая им наводящие вопросы типа: испытывает ли жидкость действие силы тяжести? если жидкость разбить на слои, будет ли верхний слой давить на нижний?
Учащиеся выдвигают различные гипотезы. Представители от каждой группы устно отчитываются о проделанной работе. Среди выдвинутых учащимися гипотез могут быть и верные, и неверные. Учитель с помощью наводящих вопросов помогает учащимся найти противоречия в неправильных гипотезах. Учитель подводит итог работы групп.
Под диктовку учителя учащиеся записывают в тетради: «На жидкость, как и на все тела на Земле, действует сила тяжести. Каждый слой (рисунок на доске) давит на нижележащий слой. Поэтому давление в точке B больше, чем давление в точке А. Жидкость действует не только на дно, но и на стенки сосуда».
3. Сообщение учителя (учебная проблема: от чего зависит давление жидкости на дно и стенки сосуда?)
4. Работа в группах. Учащиеся обсуждают поставленный вопрос и предлагают факторы, от которых может зависеть давление жидкости на дно сосуда (как правило – высота столба жидкости, её плотность, площадь дна сосуда, но могут быть и другие). Учитель останавливает внимание на тех, которые чаще предлагались, – следует проверить предположения экспериментально. 1-я и 4-я группы должны проверить, зависит ли давление жидкости от высоты её столба (слоя), а если зависит, то каков вид этой зависимости; 2-я и 5-я группы – зависит ли давление жидкости от её плотности, а если зависит, то каков вид этой зависимости; 3-я и 6-я – зависит ли давление жидкости от площади дна сосуда, а если зависит, то каков вид этой зависимости. Каждая группа получает карточку, в которой описан план действий учащихся:
1. Подумайте, как можно пронаблюдать зависимость. Составьте свой план действий.
2. Какие приборы и принадлежности необходимы для выполнения вашего задания? Возьмите их.
3. Выполните необходимые эксперименты, измерения.
4. Подтвердилась ли ваша гипотеза?
5. Сделайте выводы, подготовьте отчёт о проделанной работе.
Учащиеся самостоятельно подбирают себе оборудование из приборов, расставленных на столе учителя. 1-я и 4-я группы с помощью манометра измеряют давление жидкости на разных уровнях (выбирают манометр, сосуд с водой); 2-я и 5-я группы с помощью манометра измеряют давление жидкости на одинаковых уровнях – сначала в сосуде с водой, потом в сосуде с раствором соли (выбирают манометр, сосуд с водой и сосуд с раствором соли); 3-я и 6-я группы с помощью манометра измеряют давление жидкости на одинаковых уровнях в сосудах разной формы (выбирают манометр, сосуды разной формы т.е. с дном разной площади, с водой). После проведённых исследований представители групп выступают с отчётом.
5. Работа в группах. Вывод формул найденных зависимостей. Учитель, переходя от группы к группе, задаёт наводящие вопросы: что такое давление по определению (запишите формулу)? чему равна сила, с которой жидкость давит на дно сосуда?
В результате каждая группа должна получить:
Учитель делает заключение: «Итак, выведенная нами формула для расчёта давления жидкости на дно и стенки сосуда показывает, что давление, создаваемое слоем жидкости, зависит от плотности жидкости и высоты её слоя. При увеличении плотности жидкости и высоты её слоя давление возрастает. А сейчас вы на основе приобретённых сегодня знаний попытайтесь, пожалуйста, предсказать результат следующего опыта. У меня есть пластиковая бутылка с отверстиями на разной высоте. Как вы думаете, если я налью в неё воду, то из какого отверстия вода будет бить дальше?» Учащиеся высказывают свои предположения и объясняют их. Учитель ставит опыт. Предположения учащихся подтверждаются экспериментально.
6. Подведение итогов. Что нового вы узнали на уроке? Задание на дом – домашнее исследование: определите давление воды на дно стеклянных банок разной вместимости, ведра, ванной, кастрюли и других сосудов, которые вы найдёте у себя дома.
Наталья Викторовна Щербакова – учитель высшей квалификационной категории, почётный работник общего образования Российской Федерации, имеет сертификат аттестации учителя-экспериментатора, педагогический стаж 24 года. Использует при преподавании элементы технологии В.М.Монахова, опорные конспекты В.Ф.Шаталова, блочно-урочную систему уроков, проблемный метод обучения, игровые методы обучения в младших классах: уроки-путешествия, уроки-КВНы, «физические бои», турниры любителей физики. Большое внимание уделяет развитию опытно-исследовательских способностей учащихся старших классов, в частности, при проведении домашних ученических исследований, а также при проведении научно-практических конференций. Неоднократно её ученики становились победителями городских олимпиад по физике и занимали призовые места на городских научно-практических конференциях. В свободное время увлекается туризмом, много времени уделяет садоводству. Старшая дочь Натальи Викторовны пошла по её стопам, тоже выбрав профессию учителя.
.
.
Источник
