Относительное равновесие жидкости в сосуде

Содержание:

• Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси.

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. В состоянии равновесия в движущемся сосуде жидкость движется вместе со всем контейнером. То есть, жидкость находится в относительном состоянии покоя. Рассмотрим цилиндрический контейнер радиусом H (рис. 2.9), заполненный до определенного уровня жидкостью плотностью p и вращающийся с постоянной угловой скоростью относительно вертикальной оси.

Через некоторое время после начала вращения сосуда жидкость под действием трения вращается с той же скоростью, что и сосуд. Равновесие жидкости устанавливается для сосуда, другими словами, для неинерциальных систем координат x, y, r, которые вращаются вместе с сосудом. При написании уравнений равновесия в неинерциальных системах необходимо ввести силу подвижной инерции в число рабочих forces.

В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести. Людмила Фирмаль

• В рассматриваемом случае такая сила направлена вдоль радиуса и равна & M (центробежная сила равна n2g элементарной массы AM, которая вращается на расстоянии r от вертикали axis. In помимо центробежной силы, гравитация DM ^действует на любую частицу AM-это: за счет силы тяжести ^ = ° ;=°; ПГХ = -§; От портативной инерции п *. =<sup class=»reg»>®</sup>ГХ Риш-0)2 в> пр%= 0、 Где*и y-горизонтальные координаты произвольно выбранной точки А в жидкости. Рассмотрим 2 вопроса здесь. 39.

Форма поверхности одинакового давления. Используйте уравнение поверхности равного давления (2.10)’ Rhyh + ру ю + Rghyg-0 Когда вы назначаете ему выражения Px, Py и Pr, вы находите co2 x yx + co2 yy-diig-0. После интеграции、 гг-(* 2 + У2) §Р= С Или Х2 + У2-Г2.、 СО2-Р2 / 2 §р= с(2.23） Как видно из (2.23), поверхность равного давления в этом случае представляет собой семейство совпадающих 1-вращающихся параболоидов с вертикальной осью. Различные значения константы C соответствуют различным параболам одинакового давления.

• Свободная поверхность это также поверхность, на которой давление во всех точках равно давлению, равному внешнему давлению p0. Найти значение любой константы c параболоида свободной поверхности. Х-0; У = 0; РСВ = Р0.Если подставить эти координаты в Формулу (2.23), то: Ц0 = § 0. Уравнения свободной поверхности * С ш-Р0 = ^ (*2 +! 2. ） 2-й. Или Огнестрел-20 = СО2 Г2 / 2Д, (2.24） Частицы жидкости, находящиеся в относительном стационарном состоянии во вращающемся сосуде на расстоянии радиуса r от оси вращения, имеют линейную скорость u-(π.

Высота, на которой точка свободной поверхности выше вершины параболоида(например、 Б = РК-Р0 = СО2 Р2 /2§= С2 / 2С (2.25） 1 матч-фигура, которая будет объединена при наложении. 40. 20 ордината вершины параболоида свободной поверхности при заданной угловой скорости зависит от количества жидкости в сосуде. Если перед вращением сосуда уровень жидкости был установлен на горизонтальную и высоту H, то объем жидкости был равен 2N2H.

Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники. Людмила Фирмаль

• При вращении сосуда свободная поверхность становится параболой, форма объема жидкости изменяется, а величина при p = const{остается неизменной： | (Р0 +(r212d О2 ） О После интеграции、 Ч ■= рН + П2 К2 / 4Д Или Р0 = я-п * д * / 4#. Предполагая, что 20 = 0, мы знаем угловую скорость a, когда свободная поверхность жидкости касается дна контейнера. w = 2 Уды / я. Закон распределения давления. Используя дифференциальное уравнение жидкостных равновесий (2.5) и подставляя в него проекцию распределения плотности массовых сил, он выглядит следующим образом: гг = pY2(xc1x + ыыы) Сделай сам.

После интегрирования уравнения(2.26)、 / ? п(w2g72-ДГ)+ КБ(2.27） Если подставить координаты r = 0, r-r0 и давление p = p0 в уравнение (2.27), то получим Cp. С1! = Р0-Р (н0)= Р0 + rd0 Подставляя найденные значения C1 в(2.27), получаем 2r2 / 2d = H ‘позволяет переписать любую точку в виде (2.28). Здесь k-глубина погружения точки под свободную поверхность, то есть вертикальное расстояние от свободной параболы до точки задачи. Поэтому в жидкости, которая неподвижна в равномерно вращающемся сосуде, вертикальное давление распределяется по закону гидростатического давления.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Равновесие однородной несжимаемой жидкости относительно земли.
2. Геометрическая интерпретация основного уравнения гидростатики.
3. Силы давления покоящейся жидкости на горизонтальные и наклонные плоские площадки (стенки).
4. Силы давления покоящейся жидкости на цилиндрические стенки.

Источник

В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.

1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле

p = p0 + ρ·(g·z ± a·x),

Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:

g·z = ± a·x

или

z/x = tg α = ± a/g,

где α – угол наклона свободной поверхности жидкости к горизонту.

Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l) высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.

Если сосуд движется равномерно (а = 0), уравнение приводим к виду:

p = p0 + ρ·g·z = p0·γ

В этом случае поверхность равного давления представляет горизонтальную плоскость.

2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.

Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:

p = p0 + γ·((ω2·r2)/(2·g) – z)

Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:

z = (ω2·r2)/(2·g) = u2/(2·g),

где окружная скорость u = ω·r (r – радиус вращения точки).

Высота параболоида вращения:

h = ω2·r20/(2·g),

где r0 – радиус цилиндрического сосуда.

Сила давления жидкости на дно сосуда:

P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),

где h0 – начальная глубина жидкости в сосуде до момента его вращения.

Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).

3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.

В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.

Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).

Распределение давления по глубине жидкости определяется выражением:

p = p0 + γ·ω2·(r2 – r20)/(2·g)

где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.

Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.

Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в. Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.

Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.

Источник

05-3

Относительный покой жидкости в сосуде, движущемся с постоянным ускорением

и вращающемся вокруг вертикальной оси с постоянной угловой скоростью

Относительный покой (равновесие жидкости в движущемся сосуде)

При равновесии в движущемся сосуде жидкость движется вместе с сосудом как единое целое, т.е. находится в состоянии относительного покоя.

Сосуд, движущийся горизонтально и прямолинейно с постоянным ускорением

Рассмотрим равновесие жидкости, находящейся в сосуде, перемещающемся горизонтально с постоянным положительным ускорением .

В том случае из массовых сил действуют сила тяжести и сила инерции , направление которой противоположно направлению ускорения.

Проекция плотности распределения силы тяжести , а силы инерции .

Применим уравнение равновесия жидкости Эйлера в объединенном виде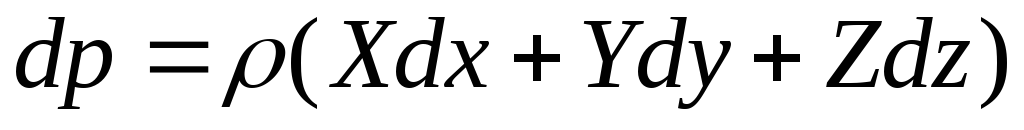

После интегрирования

При 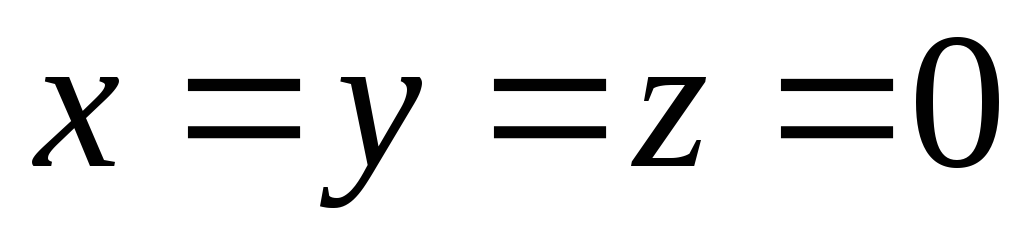имеем , окончательно .

Уравнение поверхностей равного давления из условия получим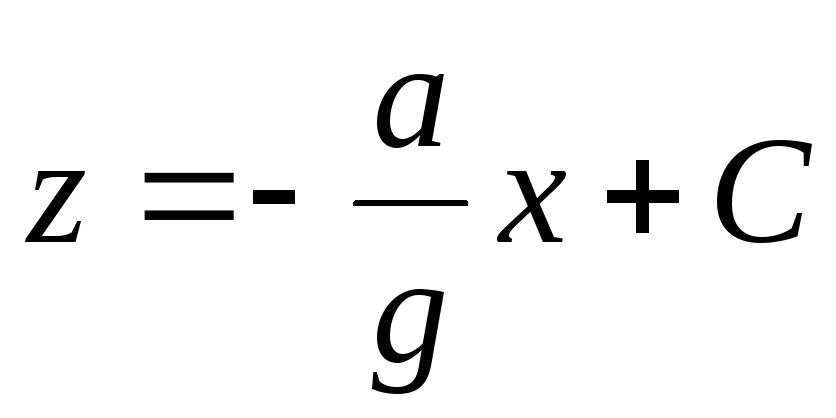. Для свободной поверхности 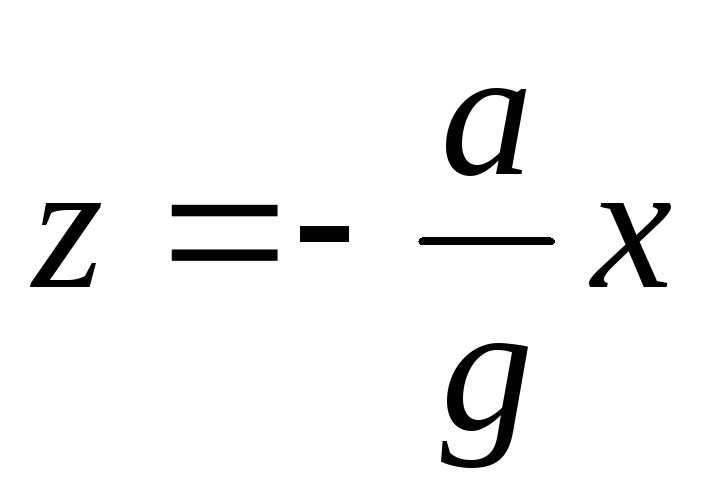. Тангенс угла наклона поверхностей равного давления (не зависит от ).

Как распределено давление по глубине ? Обозначим 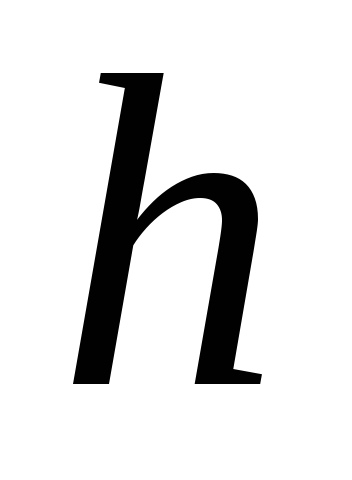– глубину точки, отсчитанную по вертикали от свободной поверхности. Тогда . Подставим в выражение для давления . Распределение давления по глубине подчиняется гидростатическому закону.

Сосуд, движущийся вертикально с постоянным ускорением

В этом случае положительные значения ускорения соответствуют ускорению, направленному вверх (по оси ), а отрицательные -когда ускорение направлено вниз.

Уравнение поверхностей равного давления .

Давление .

Цилиндрический сосуд, равномерно вращающийся относительно вертикальной оси

Проекции вектора плотности распределения массовых сил при этом:

от силы тяжести , ,

от центробежной силы инерции , , .

Применим уравнение равновесия жидкости Эйлера в объединенном виде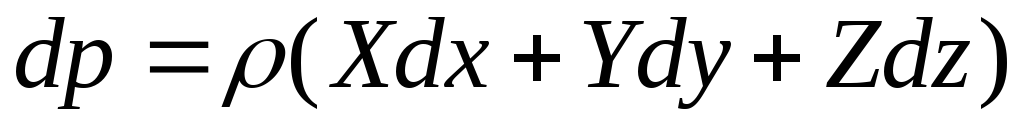

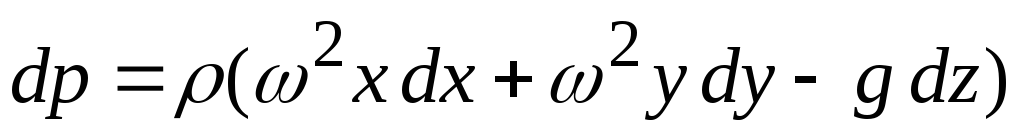
Для нахождения формы поверхностей равного давления произведем интегрирование при условии .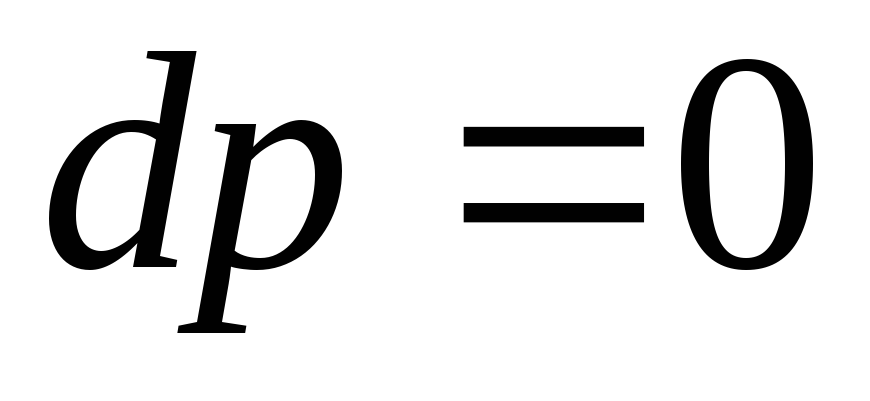

или, поскольку ,

, окончательно

Из полученной формулы ясно, что поверхности равного давления представляют собой семейство конгруэнтных параболоидов вращения с вертикальной осью. Свободная поверхность – частный случай поверхности равного давления, во всех точках которой давление равно внешнему давлению . Координаты вершины параболоида , , , . .

Уравнение свободной поверхности

Закон распределения давлений. Используем ранее полученное дифференциальное уравнение равновесия жидкости 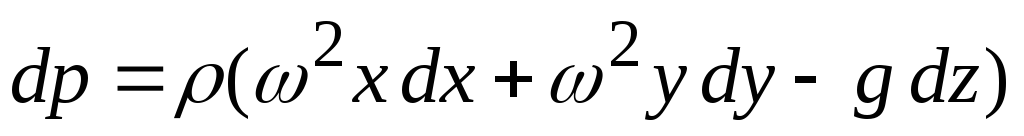. После интегрирования имеем:

. Из условий на вершине параболоида , , 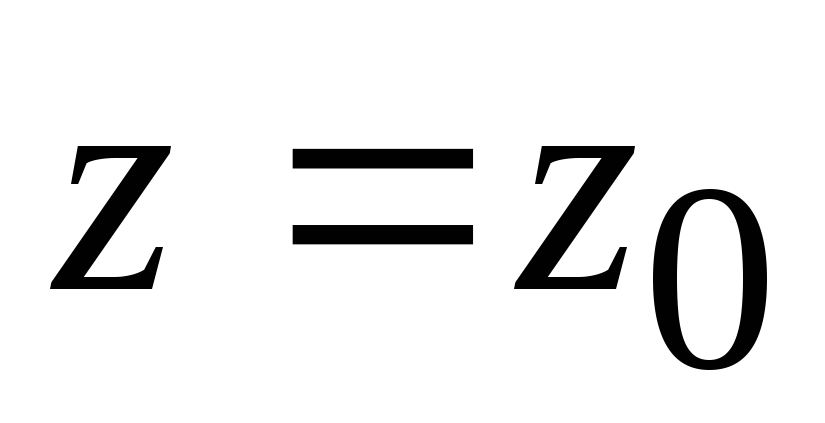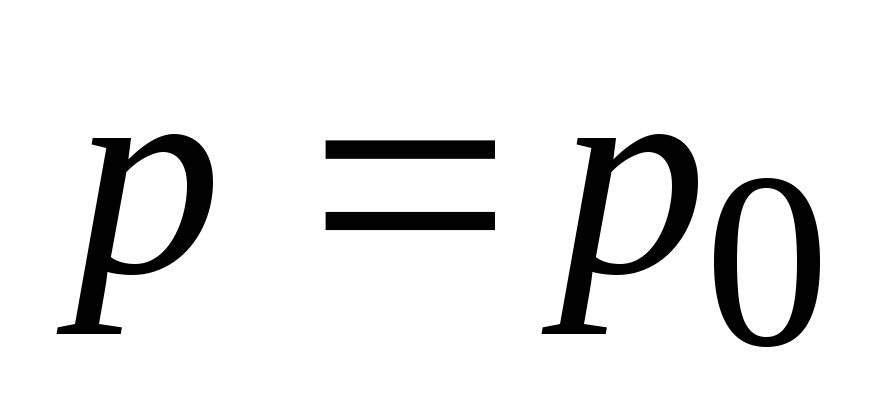найдем , после подстановки

Установим как распределяется давление по вертикали. Для этого подставим в полученное уравнение выражение из уравнения свободной поверхности .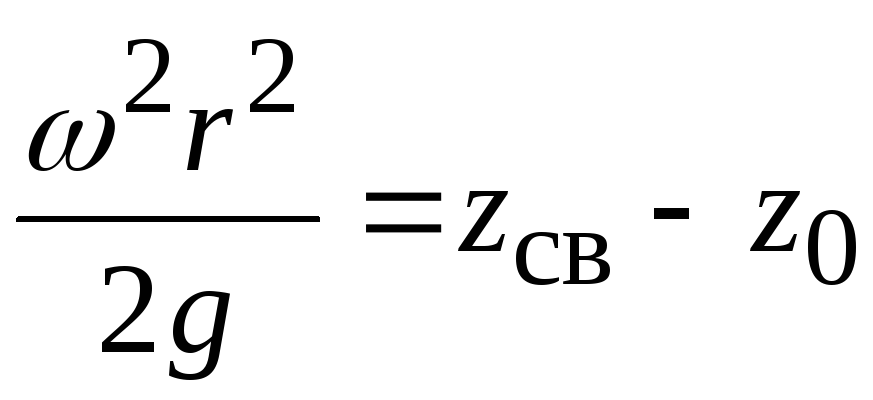

, где

– глубина погружения точки под свободной поверхностью.

Таким образом, в жидкости, покоящейся в равномерно вращающемся сосуде, давление по вертикали распределяется по гидростатическому закону.

Соседние файлы в папке Lektsii

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Источник

Гидростатика – раздел гидравлики о законах равновесия жидкости и её взаимодействии с твердыми телами и газами.

Равновесие капельных жидкостей.Под равновесием жидкости понимается отсутствие перемещения одних её частей относительно других и жидкости в целом относительно ограничивающих её стенок. При этом сам сосуд вместе с заключенной в нем жидкостью может перемещаться в любом направлении и с любым ускорением. Различают «абсолютное» и относительноеравновесие (покой) жидкости.

«Абсолютное» равновесие» – это равновесие жидкости в неподвижном относительно земли сосуде в поле только гравитационных сил. При «абсолютном» равновесии результирующая массовых сил направлена вертикально вниз.

Относительное равновесие жидкости – это равновесие её в поле силы тяжести и сил инерции. При относительном равновесии результирующая массовых сил может быть направлена в любом направлении.

Очевидно, что «абсолютное» равновесие представляет собой частный случай относительного, характеризующийся тем, что из всех массовых сип действует только сила тяжести.

В жидкости, находящейся в покое, силы трения, обусловленные вязкостью, не проявляются (не действуют касательные силы). Поэтому, реальные жидкости по своим свойствам будут очень близки к идеальным, и, следовательно, все задачи гидростатики будут решаться с большой точностью.

Гидростатическое давление.Как отмечалось ранее,на жидкость могут действовать поверхностные и массовые силы. Массовые силы в соответствии со вторым законом Ньютона про­порциональны массе жидкости или, для однородной жидкости, – ее объёму. К ним относятся сила тяжести и сила инерции переносного движения системы, действующая на жидкость при относительном ее покое (а также при ускоренном движении).

Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости на данный объем или же воздействием других тел (твердых или газообразных), соприкасающихся с данной жидкостью. Как следует из третьего закона Ньютона, с такими же силами, но в противоположном направлении, жидкость действует на соседние с нею тела.

Согласно положению теоретической механики любая система, в том числе и жидкостная, может находиться в равновесии только при условии равенства нулю равнодействующей всех приложенных к ней внешних сил, а также их результирующего момента. Состояние жидкости при этом характеризуется только внутренними (молекулярными) силами.

Рассечём жидкость воображаемой поверхностью и выделим около точки с координатами некоторую площадку величиной (рис. 2.1).

Рис. 2.1. Разложение поверхностной силы на две составляющие

В общем случае поверхностная сила , действующая в точке на площадке , направлена под некоторым углом к ней, и ее можно разложить на две силы: – нормальную сжимающую силу; и – тангенциальную силу или силу трения. Нормальная сжимающая сила может быть условно представлена в виде вектора, который направлен по внутренней нормали к выделенной площадке (т.е. внутрь объёма жидкости) и приложена к площадке в точке .

Среднее напряжение этой силы можно найти, отнеся её к площади по формуле

. (2.1)

Для определения истинного значения напряжения в точке необходимо перейти к пределу этого отношения при условии, что площадка уменьшении до нуля

. (2.2)

Нормальное напряжение силы давления, называется гидромеханическим давлением, или просто давлением, и обозначается буквой .

На внешней поверхности силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими.Таким образом, в неподвижной жидкости возможен лишь один вид напряжения – напряжение сжатия, т.е. гидростатическое давление.

Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой и выражается подобно давлению пределом отношения, а размерность его та же, что и давления,

. (2.3)

Источник