Относительный покой жидкости движение сосуда с жидкостью
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
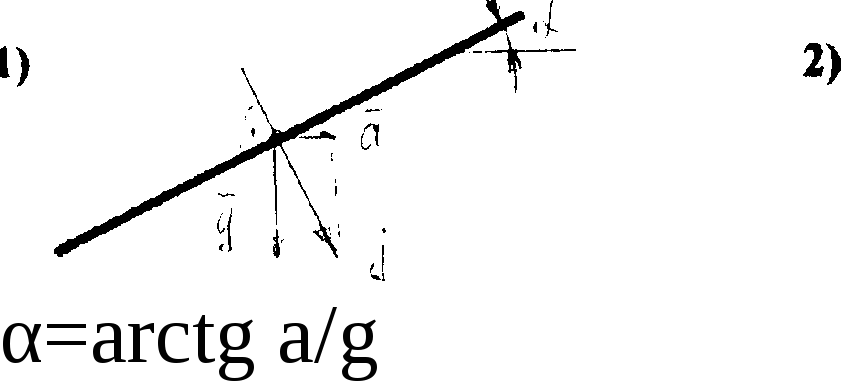
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 — высота расположения точки свободной поверхности относительно дна сосуда;
h0 — высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
3 КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
Источник
Относительным
покоем
жидкости
называется
покой жидкости относительно движущегося
сосуда, в который эта жидкость помещена.
При этом частицы жидкости нe
перемещаются относительно друг друга
и относительно сосуда, а ведут себя как
твердое тело.
Если
сосуд с жидкостью движется с постоянным
ускорением, то на жидкость кроме силы
тяжести действует постоянная по
величине сила инерции. Под действием
двух сил жидкость смещается и занимает
новое положение равновесия.
Примеры относительного
покоя жидкости: жидкость в перемещающейся
цистерне, горючее в движущемся автомобиле,
жидкость во вращающемся сосуде и т.п.
1.7.1. Прямолинейное равнопеременное движение сосуда с жидкостью
При
прямолинейном движении сосуда с
постоянным ускорением нa
жидкость действуют единичные массовые
силы: сила тяжести g
и сила инерции а.
При этом сила инерции направлена в
сторону, противоположную ускорению.
Для
определения формы и положения поверхности
жидкости следует руководствоваться
следующим свойством: равнодействующая
массовая сила всегда действует по
нормали к поверхности уровня:
и направлена перпендикулярно к свободной
поверхности жидкости.
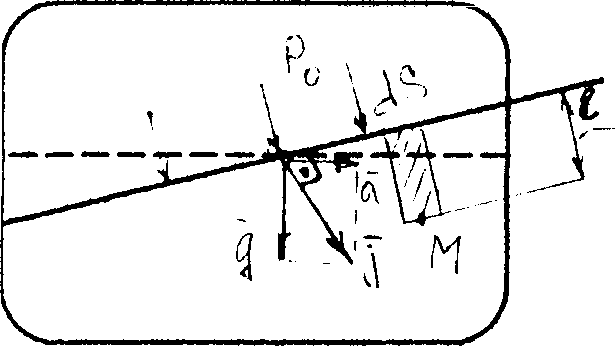Возьмем
произвольную точку М
нa
расстоянии l
от свободной поверхности уровня. Сила,
действующая нa
нее: pds
= роds
+ jρlds,
где
lds
– объем столбика жидкости.
Сократив
нa
ds,
получаем р
= ро
+ jρ1–
давление в точке М.
Давление
нa
глубине 1
равно сумме давления на свободной
поверхности жидкости и давления высоты
столбика жидкости.
Можно решить две
задачи:
1. Зная
ускорение движения сосуда, можно найти
положение поверхности жидкости.
2. Зная положение
поверхности жидкости, можно найти
ускорение движения сосуда.
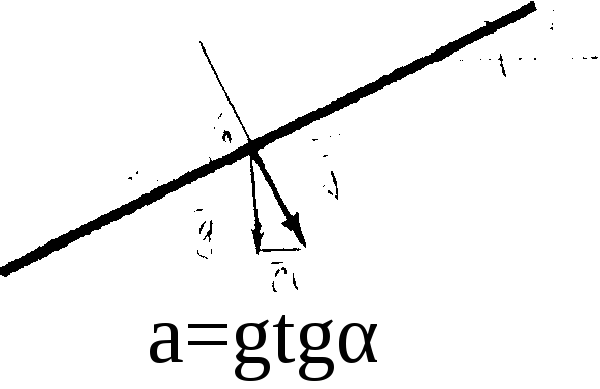
1.7.2. Равномерное вращение сосуда с жидкостью вокруг вертикальной оси
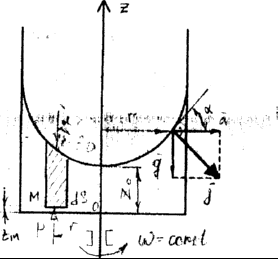
Сосуд
с жидкостью вращается с угловой скоростью
ω
= const.
Ha
жидкость действуют две единичные
массовые силы: сила тяжести g
и сила инерции а
= ω2
r.
Равнодействующая
и направлена по нормали к поверхности
жидкости.
tg
=
=
;
тогдаdz
=
dr.
Интегрируя
это выражение, получаем: z
=
+с.
Для
начальных условий r
= 0 с
= zо,
окончательно
z
=
+zo
– уравнение свободной поверхности
жидкости, параболоид вращения, вершина
которого находится на расстоянии zo
от дна сосуда.
Определим
зависимость давления в произвольной
точке жидкости как функцию от r
и z.
Условие
равновесия столбика жидкости площадью
ds
в проекции на ось Oz:
pds
– (zo
– zМ
+
)ρgds
=
,
гдеcosα
=
.
Сокращая
на ds,
получаем: р
= po
+
+ρg(zо-
zM)
– давление во вращающейся жидкости. Оно
возрастает пропорционально радиусу r
и уменьшается пропорционально высоте
zM.
1.7.3. Равномерное вращение сосуда с жидкостью вокруг горизонтальной оси
Ж
идкость
будет находиться в состоянии относительного
покоя, если сосуд вращается с очень
большой скоростью, то величина силы
инерции будет намного больше величины
силы тяжести, т. е. силой тяжести можно
пренебречь
a>>g,
где а
= ω2r;
r
– расстояние от стенки сосуда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
25.11.2019224.26 Кб0Лекции-история экон.doc
- #
- #
- #
- #
- #
- #
Источник
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 — высота расположения точки свободной поверхности относительно дна сосуда;
h0 — высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Источник
При движении сосуда в горизонтальном направлении с постоянным ускорением (рис. 4.1) на жидкость, находящуюся в нем, действует сила тяжести и сила инерции. Свободная поверхность представляет собой наклонную плоскость, уравнение которой имеет вид
где С – постоянная величина; а – ускорение сосуда.
Гидростатическое давление в любой точке жидкости
где /; – расстояние по вертикали от точки до свободной поверхности. Пьезометрическая плоскость П – П – поверхность уровня, во всех точках которой давление равно атмосферному, проходит параллельно свободной поверхности на высоте
Рис. 4.1. Схема относительного покоя жидкости при движении сосуда в горизонтальном направлении с постоянным ускорением
если давление на свободной поверхности р,> > ри (рис. 4.1), или на глубине
под свободной поверхностью жидкости, если р0а.
Сила давления на плоскую стенку в этом случае
где hc и /;?. – расстояния по вертикали от центра тяжести стенки до свободной поверхности жидкости и до пьезометрической плоскости соответственно.
Сила давления на криволинейную поверхность (рис. 4.2) может быть найдена из условия динамического равновесия объема жидкости V, заключенного между криволинейной поверхностью и плоскостью, проведенной через граничный контур поверхности (на рис. 4.2 этот объем заштрихован):
Рис. 4.2. Схема для определения силы давления на криволинейную поверхность
где Р| – сила давления на плоское сечение АВ. определяемая по формуле (4.3); F = paW – сила инерции; G = pgW– вес объема жидкости.
При вращении сосуда вокруг вертикальной оси z (рис. 4.3) на любую частицу жидкости кроме силы тяжести действует также центробежная сила инерции
которую можно разложить на составляющие
где Ат – масса частицы; со – угловая скорость; г – расстояние частицы от оси вра-
—>
щения, х и у – проекции вектора у – на координатные оси, причем х2 + у2 = г2.
Следовательно, проекции ускорения массовых сил на координатные оси в рассматриваемом случае равновесия жидкости равны
Подставив эти значения X, У и Z в дифференциальное уравнение равновесия (2.1) и выполнив интегрирование, получим
гдеря- давление на свободной поверхности, го – вершина параболоида вращении.
В произвольной точке, расположенной на глубине /; под поверхностью жидкости, давление
Поверхности уровня представляют собой параболоиды вращения. Уравнение свободной поверхности жидкости имеет вид
Пьезометрическая поверхность при р = р„ совпадает со свободной поверхностью жидкости. Если свободная поверхность отсутствует (закрытый сосуд полностью заполнен жидкостью под давлением), то пьезометрическая поверхность проходит через точку жидкости, в которой давление равно атмосферному (например, через уровень в открытом пьезометре, где р = pj.
Если R – радиус сосуда, а со – угловая скорость, то высота параболоида вращения
Объем параболоида вращения
Примеры расчетов
Пример 4.1 В цилиндрическую форму (рис. 4.3) с внутренним диаметром D = 1120 мм и высотой / = 1000 мм, вращающуюся при п = 500 об/мин, залит цементный раствор (литой) р = 1600 кг/м3 для изготовления трубы центробежным способом. При толщине стенки цементной трубы 5| = 60 мм определить толщину стенки трубы 52 у верхней торцовой стенки формы [7].
Рис. 4.3. Схема к примеру 4.1
Таким образом, толщина стенки трубы в верхней ее части меньше на 7 мм. В случае необходимости уменьшения разницы между 5| и 5: необходимо повысить угловую скорость вращения формы, т.е. число оборотов в минуту п.
Пример 4.2. Определить длину пути разгона L автомобиля-самосвала от скорости Vo = 0 до и = 40 км/ч и максимальное ускорение а, при котором цементный раствор (р = 2200 кг/м3) не выплеснется из кузова, длина которого I = 2,6 м, ширина 6=1,8 м и высота h = 0,8 м (рис. 4.4). Раствор заполняет кузов на У4 его высоты. С какой силой при этом ускорении цементный раствор действует на задний борт кузова? Движение автомобиля – прямолинейное, равноускоренное [13].
Рис. 4.4. Схема к примеру 4.2
Решение. В данном случае на жидкость действуют две силы: сила тяжести G, направленная вниз, и сила инерции F = та, направленная влево. Подставим в дифференциальное уравнение поверхности уровня значения X = – a, Y =0,
Z = -g:
После интегрирования получаем
где — = tg(p – тангенс угла наклона свободной поверхности жидкости к гори- 8
зонту, значение которого в условиях данной задачи не может превзойти величину
Следовательно, максимальное ускорение автомобиля
Длину пути разгона автомобиля находим из уравнений равноускоренного движения:
Сила давления раствора на задний борт
Задачи
Задача 4.1. Открытый цилиндрический резервуар заполнен водой до высоты Я = 2 м (рис. 4.5). Диаметр резервуара D = 1,2 м, температура жидкости 20 °С. Определить: 1) объем жидкости, сливающейся из резервуара при его вращении с частотой п = 2,1 с’1 вокруг его вертикальной оси; 2) силу давления на дно резервуара и горизонтальную силу, разрывающую резервуар по сечению 1-1 при его вращении [27].
Рис. 4.5. Схема к задаче 4.1
Задача 4.2. Цилиндрический сосуд диаметром D = 30 см и высотой Н = 42 см полностью заполнен водой, температура которой 20 °С (рис. 4.6). Диаметр отверстия сверху равен d = 24 см. Определить: 1) с какой предельной частотой можно вращать сосуд около его вертикальной оси, чтобы в сосуде осталось 75 % первоначального объема воды; 2) силу давления на дно сосуда и горизонтальную силу, разрывающую сосуд по сечению 1-1 при его вращении с определенной частотой [27].
Рис. 4.6. Схема к задаче 4.2
Задача 4.3. В сосуд (рис. 4.7) высотой Н = 0,3 м залита вода до уровня /; = 0,2 м. Определить, до какой угловой скорости со можно раскрутить сосуд, с тем чтобы жидкость не выплеснулась из него, если его диаметр D = 100 мм [5].
Рис. 4.7. Схема к задаче 4.3
Задача 4.4. Цилиндрическая цистерна наполнена бензином, температура которого I =20 °С (рис. 4.8). Диаметр цистерны D = 1,74 м, длина L = 3,26 м. Глубина бензина в горловине h = 20 см, ее диаметр d = 30 см. Определить силы давления на плоские торцевые стенки А и В цистерны в двух случаях: 1) когда цистерна не движется; 2) при движении цистерны горизонтально с положительным ускорением а = 4,37 м/с” [27].
Рис. 4.8. Схема к задаче 4.4
Задача 4.5. В кузов автомобиля-самосвала (рис.4.9) до уровня /г, = 0,4 м налит цементный раствор. Определить наименьший допустимый путь торможения самосвала от скорости о = 36 км/ч до остановки исходя из условия, что раствор не выплеснулся из кузова. Для упрощения принять, что кузов самосвала имеет форму прямоугольной коробки размерами / = 2,5 м; И = 0,8 м; ширина кузова h = 1,8 м, а движение автомобиля при торможении равнозамедленное [26].
Рис. 4.9. Схема к задаче 4.5
Задача 4.6. Определить минимальную частоту вращения /г, которую нужно сообщить сосуду, изображенному на схеме, вокруг его вертикальной оси для полного его опорожнения (рис 4.10). Размеры: D = 200 мм; d= 100 мм; Н= 50 мм [26].
Рис. 4.10. Схема к задаче 4.6
Источник