Относительный покой жидкости в движущихся сосудах
Относительным
покоем
жидкости
называется
покой жидкости относительно движущегося
сосуда, в который эта жидкость помещена.
При этом частицы жидкости нe
перемещаются относительно друг друга
и относительно сосуда, а ведут себя как
твердое тело.
Если
сосуд с жидкостью движется с постоянным
ускорением, то на жидкость кроме силы
тяжести действует постоянная по
величине сила инерции. Под действием
двух сил жидкость смещается и занимает
новое положение равновесия.
Примеры относительного
покоя жидкости: жидкость в перемещающейся
цистерне, горючее в движущемся автомобиле,
жидкость во вращающемся сосуде и т.п.
1.7.1. Прямолинейное равнопеременное движение сосуда с жидкостью
При
прямолинейном движении сосуда с
постоянным ускорением нa
жидкость действуют единичные массовые
силы: сила тяжести g
и сила инерции а.
При этом сила инерции направлена в
сторону, противоположную ускорению.
Для
определения формы и положения поверхности
жидкости следует руководствоваться
следующим свойством: равнодействующая
массовая сила всегда действует по
нормали к поверхности уровня:
![]() и направлена перпендикулярно к свободной
и направлена перпендикулярно к свободной
поверхности жидкости.
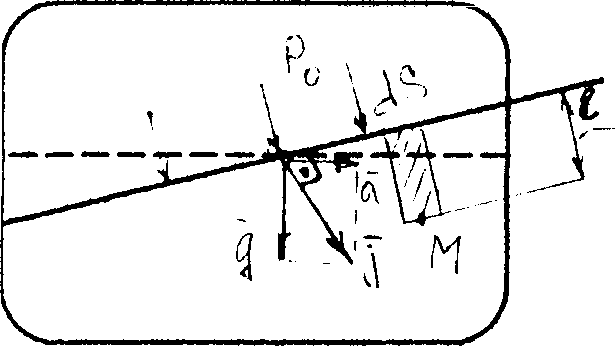 Возьмем
Возьмем
произвольную точку М
нa
расстоянии l
от свободной поверхности уровня. Сила,
действующая нa
нее: pds
= роds
+ jρlds,
где
lds
– объем столбика жидкости.
Сократив
нa
ds,
получаем р
= ро
+ jρ1–
давление в точке М.
Давление
нa
глубине 1
равно сумме давления на свободной
поверхности жидкости и давления высоты
столбика жидкости.
Можно решить две
задачи:
1. Зная
ускорение движения сосуда, можно найти
положение поверхности жидкости.
2. Зная положение
поверхности жидкости, можно найти
ускорение движения сосуда.
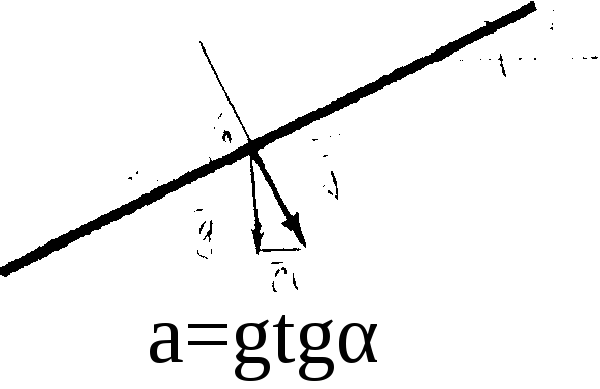
1.7.2. Равномерное вращение сосуда с жидкостью вокруг вертикальной оси
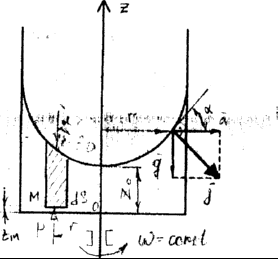
Сосуд
с жидкостью вращается с угловой скоростью
ω
= const.
Ha
жидкость действуют две единичные
массовые силы: сила тяжести g
и сила инерции а
= ω2
r.
Равнодействующая
![]() и направлена по нормали к поверхности
и направлена по нормали к поверхности
жидкости.
tg
=
![]()
=![]() ;
;
тогдаdz
=
![]() dr.
dr.
Интегрируя
это выражение, получаем: z
=
![]() +с.
+с.
Для
начальных условий r
= 0 с
= zо,
окончательно
z
=
![]() +zo
+zo
– уравнение свободной поверхности
жидкости, параболоид вращения, вершина
которого находится на расстоянии zo
от дна сосуда.
Определим
зависимость давления в произвольной
точке жидкости как функцию от r
и z.
Условие
равновесия столбика жидкости площадью
ds
в проекции на ось Oz:
pds
– (zo
– zМ
+![]() )ρgds
)ρgds
=
![]() ,
,
гдеcosα
=![]() .
.
Сокращая
на ds,
получаем: р
= po
+
![]() +ρg(zо-
+ρg(zо-
zM)
– давление во вращающейся жидкости. Оно
возрастает пропорционально радиусу r
и уменьшается пропорционально высоте
zM.
1.7.3. Равномерное вращение сосуда с жидкостью вокруг горизонтальной оси
Жидкость
будет находиться в состоянии относительного
покоя, если сосуд вращается с очень
большой скоростью, то величина силы
инерции будет намного больше величины
силы тяжести, т. е. силой тяжести можно
пренебречь
a>>g,
где а
= ω2r;
r
– расстояние от стенки сосуда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать
различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
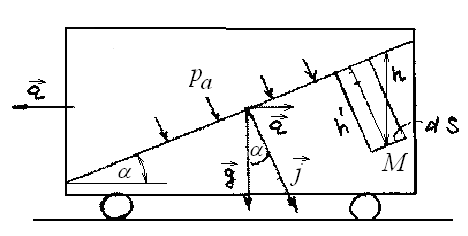
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l)
высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r — радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в.
Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
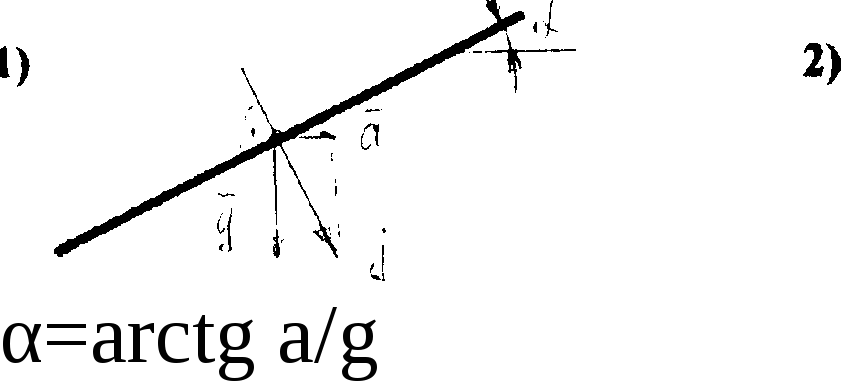
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 — высота расположения точки свободной поверхности относительно дна сосуда;
h0 — высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
3 КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
Источник
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 — высота расположения точки свободной поверхности относительно дна сосуда;
h0 — высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Источник
Гидростатикой
называется раздел гидромеханики, в
котором изучаются законы равновесия
жидкостей и их практические приложения.
Свойства гидростатического давления
Как
отмечалось ранее, жидкость в общем
случае может находиться под действием
двух сил – силы давления и массовых
сил, определяемых характером переносного
движения. В неподвижной жидкости возможен
лишь один вид напряжения – напряжение
сжатия. Механические различия между
идеальной и вязкой жидкостью начинают
проявляться только при их течении.
Действующее
на внешнюю поверхность жидкости давление
обладает следующими свойствами:
1) давление
всегда направлено по внутренней нормали
к выделенной поверхности (это следует
из определения давления);
2) в
любой точке внутри жидкости давление
по всем направлениям одинаково. Другими
словами, величина давления в точке не
зависит от ориентации площадки, на
которую действует давление;
3) для
жидкости, находящейся в состоянии
равновесия, справедлив закон
Паскаля:
всякое изменение давления в какой-либо
точке жидкости передается
без изменения во все остальные точки
жидкости. На этом свойстве основано
действие гидравлических машин
(гидропрессы, силовые цилиндры,
гидродомкраты).
Основное уравнение гидростатики
1. Абсолютный
покой жидкости.
Рассмотрим равновесие жидкости в
состоянии абсолютного
покоя, т.е.
когда на жидкость действует только сила
тяжести. Давление на свободную поверхность
жидкости равно атмосферному давлению
![]() .
.
Определим
давление
![]() в произвольно
в произвольно
выбранной точке М,
расположенной
на глубине
![]()
(рис. 1.3).
Для этогорассмотрим
равновесие жидкого тела, ограниченного
снизу площадкой
![]() .
.
Давление на основание выделенного
объема будет внешним по отношению к
жидкому телу и будет направлено
вертикально вверх. Запишем уравнение
равновесия в проекции на вертикальную
ось тела:
![]() ,
,
т.е.
![]() .
.
(1.16)
Получили
основное
уравнение гидростатики.
Д

Рис. 1.3.
К выводу основного уравнения
гидростатики для абсолютного
покоя
авление во всех точках свободной
поверхности одинаково и равно
![]() ,следовательно,
,следовательно,
давление во всех точках жидкости на
глубине hтакже
одинаково согласно основному уравнению
гидростатики. Поверхность, давление на
которой постоянно, называется поверхностью
уровня.
В данном случае поверхности уровня –
горизонтальные плоскости. Выберем
горизонтальную отсчетную плоскость,
проходящую на расстоянии
![]()
от свободной поверхности, тогда уравнение
(1.16) приобретает вид
![]()
или
![]() . (1.17)
. (1.17)
Все
члены уравнения (1.17) имеют линейную
размерность и носят название:
![]()
– геометрическая
высота,
![]()
– пьезометрическая
высота.
Величина
![]()
называется гидростатическим
напором
и согласно (1.17) при абсолютном покое
жидкости постоянна.
2. Относительный
покой жидкости.
Состояние равновесия жидкости при
наличии переносного движения называется
относительным
покоем
жидкости. Относительный покой сводится
к двум возможным видам равновесия
жидкости.
Равновесие
жидкости при равномерно ускоренном
прямолинейном
движении сосуда
Примером
может служить равновесие жидкости в
цистерне, движущейся с некоторым
ускорением
![]()
(рис. 1.4, а).
В
этом случае на жидкость будут действовать
сила тяжести и сила инерции равномерно
укоренного движения цистерны:
![]() ,
,
где
![]()
– равнодействующая единичная массовая
сила,
![]()
– единичная массовая сила переносного
движения.

а б
Рис. 1.4.
К выводу основного уравнения гидростатики
для относительного покоя:
а – равномерно
ускоренное прямолинейное движение
сосуда; б – равномерное
вращение
сосуда
При
движении цистерны начальное положение
свободной поверхности жидкости изменится.
Так как равнодействующий вектор массовых
сил должен быть направлен по внутренней
нормали к свободной поверхности жидкости,
то новое положение свободной поверхности
жидкости будет перпендикулярно вектору
![]() .
.
Наклон свободной поверхности жидкости
к горизонтальной плоскости определяется
соотношением ускорений
![]() :
:
![]() .
.
Найдем
условия равновесия жидкого объема,
имеющего в основании малую площадку
![]()
в точке М,
расположенной
внутри жидкости на глубине
![]() под
под
уровнем свободной поверхности:
![]() ,
,
или
![]() .
.
Здесь
![]()
(h–
погружение точки М
под
уровень свободной поверхности жидкости,
измеряемое по вертикали), так как
![]() ,
,
![]() .
.
Приходим к уравнению равновесия жидкости
![]() ,
,
совпадающему по
виду с записью основного закона
гидростатики (1.16).
Таким
образом, давление в любой точке жидкости
будет зависеть только от положения этой
точки относительно уровня свободной
поверхности жидкости. Поверхности
равного давления будут параллельны
свободной поверхности жидкости и иметь
такой же уклон
![]() .
.
Равновесие
жидкости в равномерно вращающемся
сосуде
Свободная
поверхность жидкости, залитой в
цилиндрический сосуд и находящейся под
действием сил тяжести, примет форму
горизонтальной плоскости на некотором
уровне
![]() относительно
относительно
дна сосуда. После того как мы приведем
сосуд во вращение вокруг его вертикальной
оси с некоторой постоянной угловой
скоростью
![]() const,
const,
форма
свободной поверхности жидкости изменится:
в центре сосуда уровень понизится, а по
краям сосуда повысится, вследствие
действия силы инерции, создающей
ускорение переносного движения
![]() ,
,
направленное в сторону стенок сосуда
(рис. 1.4, б).
Выберем
любую точку жидкости на глубине под
свободной поверхностью
![]() (в
(в
частности, точка находится на дне
сосуда), тогда давление в ней будет
![]() .
.
Этот
вывод можно распространить и на более
сложные случаи вращения сосуда. Наклоняя
ось его вращения под углом к горизонту,
результат получим тот же, что подтверждает
универсальность основного уравнения
гидростатики.
Пример 1.3. Найти
форму поверхности жидкости во вращающемся
сосуде (рис. 1.4, б).
Решение.
В каждой точке поверхности вектор
углового ускорения
![]()
будет направлен под некоторым углом
![]() по
по
отношению к касательной плоскости,
проходящей через данную точку
свободной поверхности:
![]() ,
,
или после
интегрирования
![]() ,
,
где
![]()
– координата самой низкой точки,
расположенной в центре на оси вращения.
Итак, получили,
что свободная поверхность жидкости,
находящейся в равномерно вращающемся
вокруг его вертикальной оси сосуде,
будет иметь вид параболоида вращения.
Пример
1.4. Конструкция подводного аппарата
выдерживает избыточное давление до
10 МПа. Определить максимальную рабочую
глубину погружения аппарата.
Решение.
Из основного уравнения гидростатики
имеем
![]() ,
,
т.
е.
![]() 10106/(9989.81)
10106/(9989.81)
= 1021 м.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
