Относительный покой жидкости в сосуде
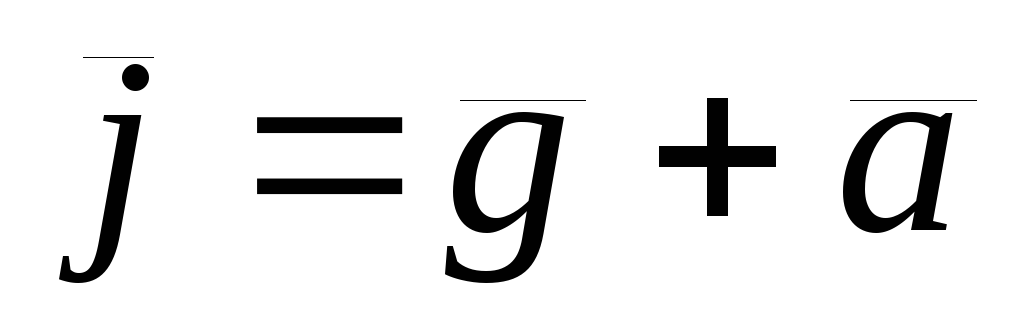
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила – сила тяжести, то при относительном покое появляется новая – сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 – высота расположения точки свободной поверхности относительно дна сосуда;
h0 – высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай – вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.

3 КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
Источник
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила – сила тяжести, то при относительном покое появляется новая – сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Из геометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
,
где z0 – высота расположения точки свободной поверхности относительно дна сосуда;
h0 – высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай – вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Источник
Относительным покоем жидкости называется покой жидкости относительно движущегося сосуда, в который эта жидкость помещена. При этом частицы жидкости нe перемещаются относительно друг друга и относительно сосуда, а ведут себя как твердое тело.
Если сосуд с жидкостью движется с постоянным ускорением, то на жидкость кроме силы тяжести действует постоянная по величине сила инерции. Под действием двух сил жидкость смещается и занимает новое положение равновесия.
Примеры относительного покоя жидкости: жидкость в перемещающейся цистерне, горючее в движущемся автомобиле, жидкость во вращающемся сосуде и т.п.
1.7.1. Прямолинейное равнопеременное движение сосуда с жидкостью
При прямолинейном движении сосуда с постоянным ускорением нa жидкость действуют единичные массовые силы: сила тяжести g и сила инерции а. При этом сила инерции направлена в сторону, противоположную ускорению.
Для определения формы и положения поверхности жидкости следует руководствоваться следующим свойством: равнодействующая массовая сила всегда действует по нормали к поверхности уровня: 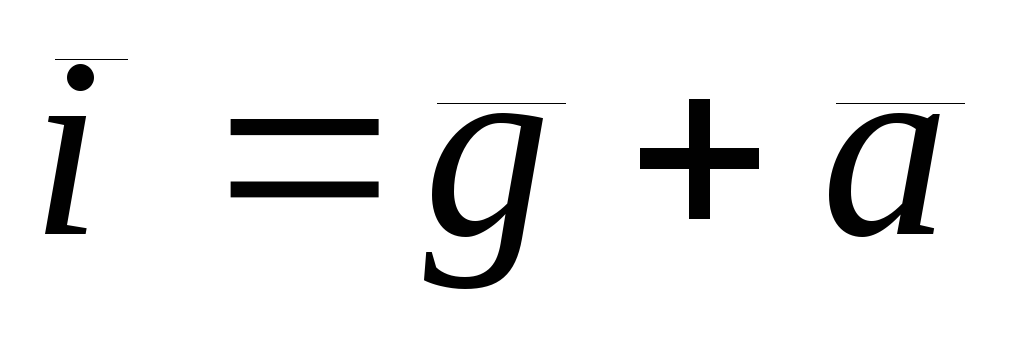 и направлена перпендикулярно к свободной поверхности жидкости.
и направлена перпендикулярно к свободной поверхности жидкости.
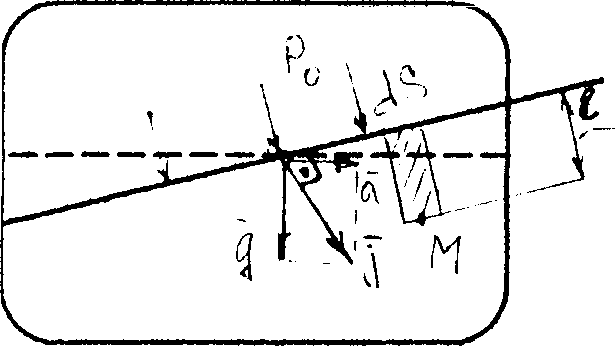 Возьмем произвольную точку М нa расстоянии l от свободной поверхности уровня. Сила, действующая нa нее: pds = роds + jρlds,
Возьмем произвольную точку М нa расстоянии l от свободной поверхности уровня. Сила, действующая нa нее: pds = роds + jρlds,
где lds – объем столбика жидкости.
Сократив нa ds, получаем р = ро + jρ1- давление в точке М.
Давление нa глубине 1 равно сумме давления на свободной поверхности жидкости и давления высоты столбика жидкости.
Можно решить две задачи:
1. Зная ускорение движения сосуда, можно найти положение поверхности жидкости.
2. Зная положение поверхности жидкости, можно найти ускорение движения сосуда.
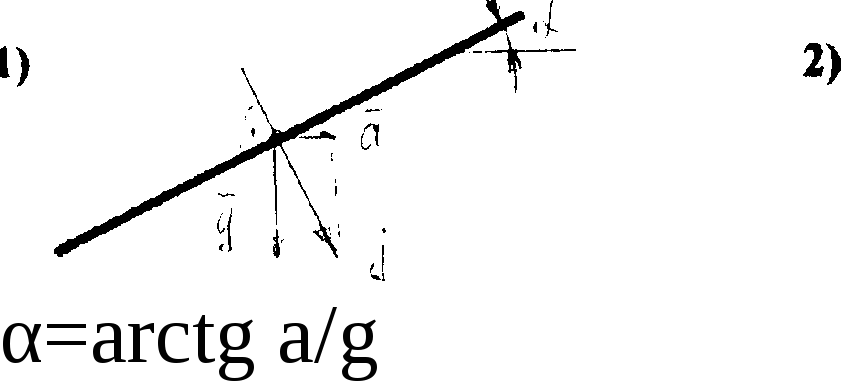
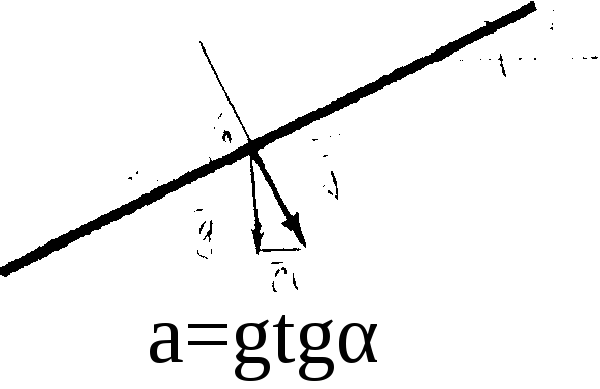
1.7.2. Равномерное вращение сосуда с жидкостью вокруг вертикальной оси
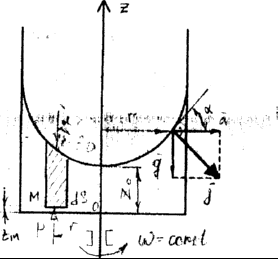
Сосуд с жидкостью вращается с угловой скоростью ω = const.
Ha жидкость действуют две единичные массовые силы: сила тяжести g и сила инерции а = ω2 r.
Равнодействующая 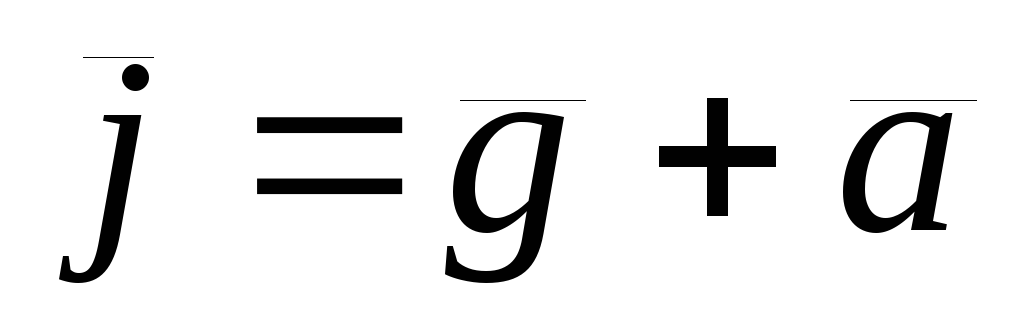 и направлена по нормали к поверхности жидкости.
и направлена по нормали к поверхности жидкости.
tg = 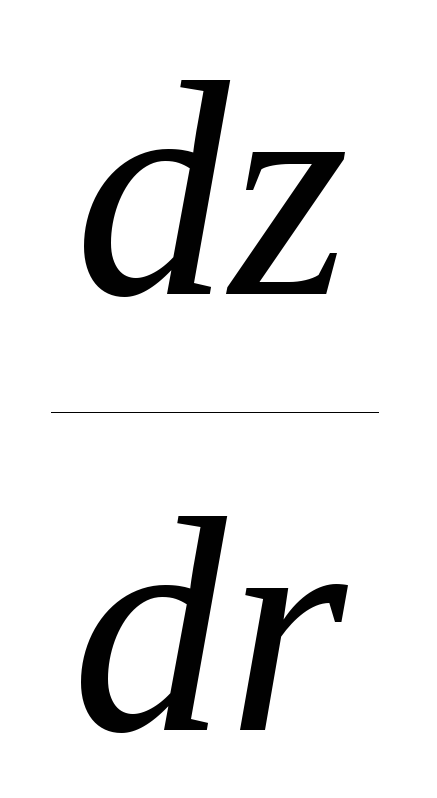 =
=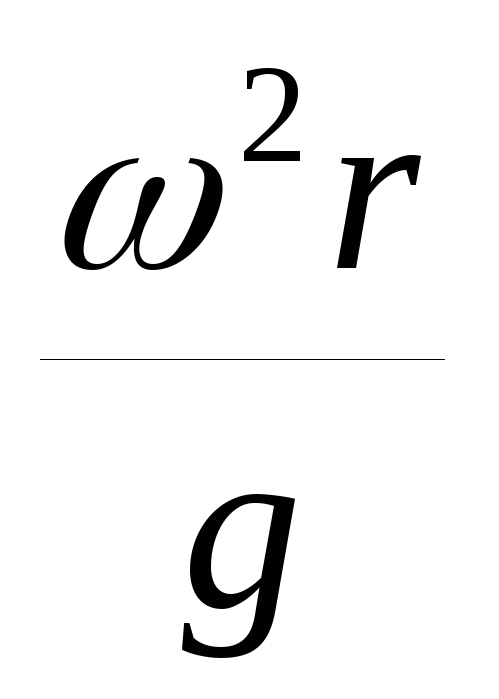 ; тогдаdz =
; тогдаdz = 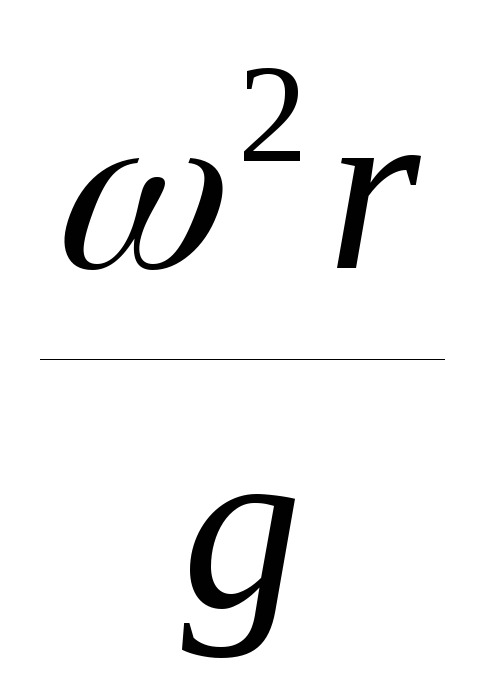 dr.
dr.
Интегрируя это выражение, получаем: z = 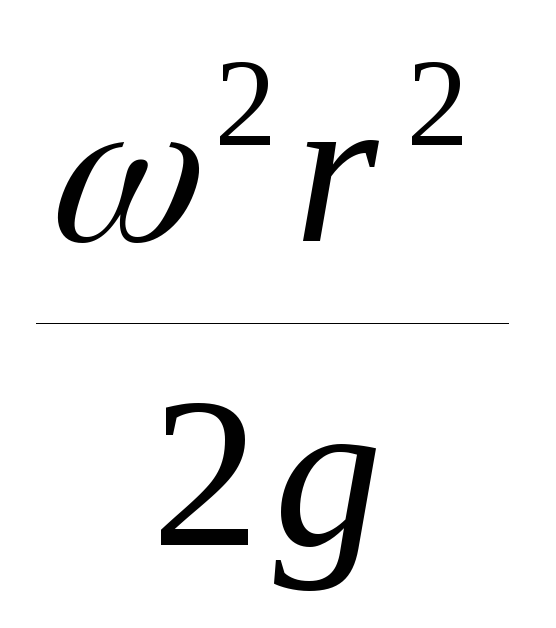 +с.
+с.
Для начальных условий r = 0 с = zо, окончательно
z = 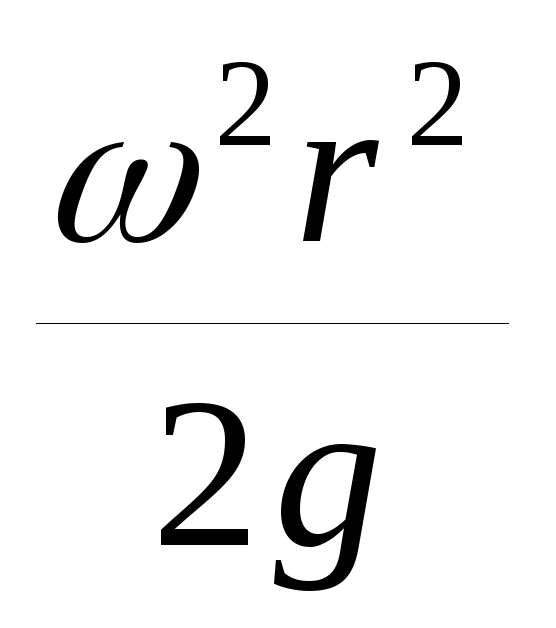 +zo – уравнение свободной поверхности жидкости, параболоид вращения, вершина которого находится на расстоянии zo от дна сосуда.
+zo – уравнение свободной поверхности жидкости, параболоид вращения, вершина которого находится на расстоянии zo от дна сосуда.
Определим зависимость давления в произвольной точке жидкости как функцию от r и z.
Условие равновесия столбика жидкости площадью ds в проекции на ось Oz:
pds – (zo – zМ +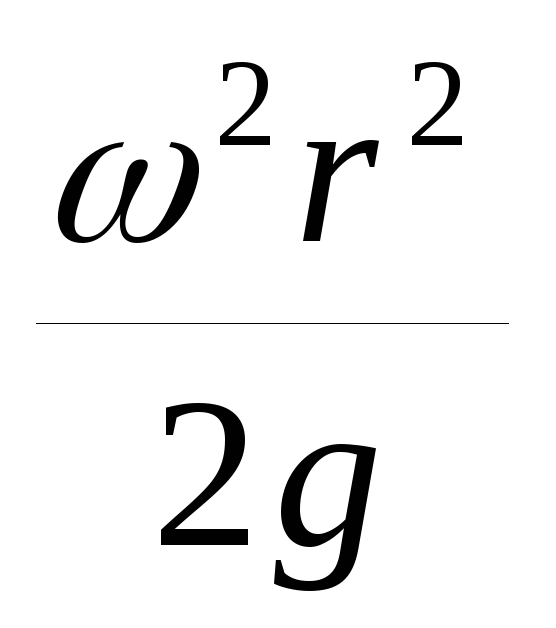 )ρgds =
)ρgds = 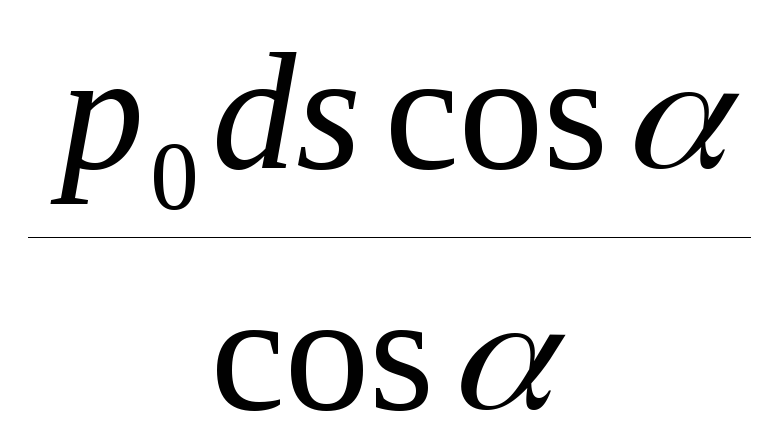 , гдеcosα =
, гдеcosα = .
.
Сокращая на ds, получаем: р = po + 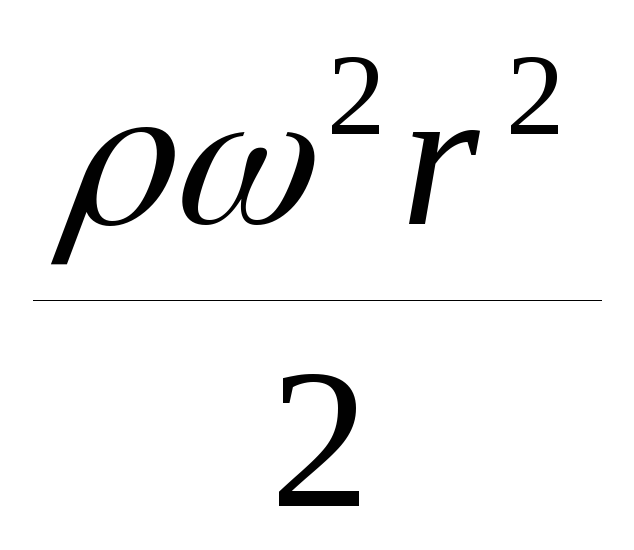 +ρg(zо- zM) – давление во вращающейся жидкости. Оно возрастает пропорционально радиусу r и уменьшается пропорционально высоте zM.
+ρg(zо- zM) – давление во вращающейся жидкости. Оно возрастает пропорционально радиусу r и уменьшается пропорционально высоте zM.
1.7.3. Равномерное вращение сосуда с жидкостью вокруг горизонтальной оси
Жидкость будет находиться в состоянии относительного покоя, если сосуд вращается с очень большой скоростью, то величина силы инерции будет намного больше величины силы тяжести, т. е. силой тяжести можно пренебречь
a>>g, где а = ω2r; r – расстояние от стенки сосуда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6). 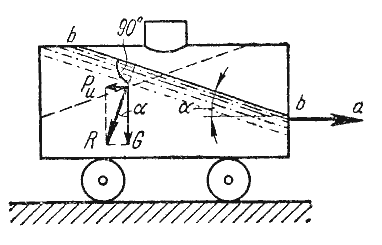
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu= mω2r, где r – расстояние частицы от оси вращения, а ω – угловая скорость вращения сосуда.
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
Рис. 2.7. Вращение сосуда с жидкостью
С другой стороны: 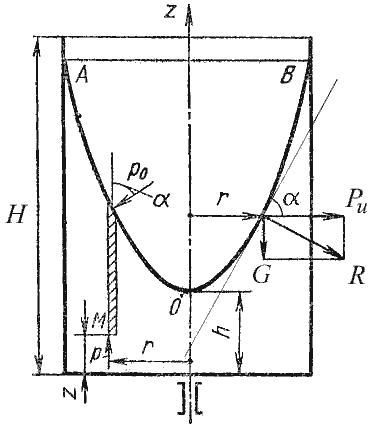
где z – координата рассматриваемой точки. Таким образом, получаем:
откуда
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z= h = C, поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Понятие относительного покоя. В предшествующем изложении гидростатики предполагалось, что жидкость находится в покое относительно некоторой условно неподвижной системы отсчета (в так называемом абсолютном покое). Неподвижными относительно этой системы предполагаются также сосуды, в которых заключена жидкость. При таком предположении и получено основное уравнение гидростатики.
Перейдем к рассмотрению так называемого относительного покоя жидкости. Под этим определением подразумевается, что частицы жидкости, заключенной в некотором сосуде, не имеют перемещений друг относительно друга и вся масса жидкости покоится относительно стенок сосуда, следовательно, относительно жестко связанных с сосудом координатных осей, в то же время сосуд перемещается произвольным образом относительно неподвижной системы отсчета.
Из основ механики известно, что законы, описывающие абсолютный или относительный покой (а также абсолютное или относительное движение), не различаются между собой, если подвижная система отсчета перемещается относительно неподвижной инерциальным образом, т.е. прямолинейно и равномерно. Рассмотрим два примера относительного покоя жидкости.
Относительный покой однородной жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси. Подвижные координатные оси расположим так, что ось Oz направлена вертикально вверх (рис. 2.17). Сосуд, благодаря трению, вовлекает в движение наполняющую его жидкость и по истечении небольшого промежутка времени, после начала вращения, жидкость также начинает приходить во вращение с той же угловой скоростью, что и сам сосуд. Таким образом, в дальнейшем жидкость покоится относительно сосуда, что позволяет применить уравнения гидростатики, но в координатах, жестко связанных с сосудом, т.е. вращающихся в пространстве.
Приложенными к частицам жидкости массовыми силами являются по-прежнему силы тяжести, параллельные оси z; силами инерции Fи в переносном движении в данном случае являются центробежные силы, перпендикулярные к оси z, имеющие ускорение (ω2r), где r = √(x2 + у2) есть расстояние данной частицы жидкости от оси вращения. Проекциями ускорения равнодействующей этих сил на оси координат будут X=│Fи/m│x= ω2x ; Y=│Fи/m│y= ω2y ; Z=│Fи/m│z= ω2z ;
Подставляя эти выражения в (2.8), найдем дифференциальное уравнение поверхностей уровня
ω2(xdx + ydy) – gdz =0. (2.21)
Интегрируя это уравнение, получим ω2/2(x2 + y2) – gz =const или ω2r2/2 – gz = const (2.22)
Из (2.22) следует, что поверхности уровня (в том числе и свободная поверхность) являются параболоидами вращения (см. рис. 1.17) вокруг оси z.
Напомним, что распределению давления в несжимаемой жидкости соответствует зависимость (2.4).
 dp =p(Xdx+Ydy + Zdz),
dp =p(Xdx+Ydy + Zdz),
а в данном случае dp = р ,
отсюда (после интегрирования) можно получить
р = р ω2r2/2 – pgz+c. (2.23)
Поместим начало подвижных координат в точку «О» пересечения оси z со свободной поверхностью. Тогда постоянная интегрирования определится из граничного условия р = р0 при r = 0 и Z= 0. Подставив эти значения в (2.23), получим const = р0, следовательно р = р0 +р* ω2r2/2 – pgz. (2.24)
Последнее уравнение выражает закон распределения давления в жидкости.
Из уравнения (2.24) видно, что давление в некоторой горизонтальной плоскости z=const по мере увеличения радиуса увеличивается по сравнению с гидростатическим, вычисленным для неподвижного сосуда, на величину p *ω2r2/2 , т.е. тем сильнее, чем больше число оборотов сосуда. Этим пользуются в технике в случаях, когда надо увеличить на некоторый период времени давление внутри массы жидкости (увеличение давления, зависящее от значения центробежной силы, лежит также в основе работы центробежных насосов).
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Источник
