Относительный покой жидкости во вращающемся сосуде

Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.

Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.

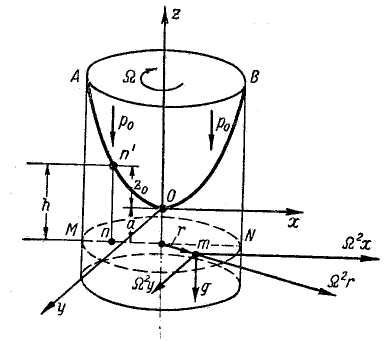
Относительный покой жидкости во вращающемся сосуде

Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz

АОВ — свободная поверхность жидкости

Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).

В эти уравнения входит объемная сила , действующая на единицу массы жидкости. В данном случае сила будет слагаться из двух сил: силы тяжести и центробежной силы.

С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет

I’= , (2-62)

где υ – скорость движения массы δM по окружности радиуса r.

Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,

I = = Ω2r. (2-63)

Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат

Ix = Ω2rcos(r,x) = Ω2x

Iy = Ω2rcos(r,y) = Ω2y

Iz = 0 (2-64)

Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем

= 0 +Ω2x = Ω2x;

= 0 + Ω2y = Ω2y;

= – (2-65)

Подставляя (2-65) в (2-17), найдем

dpA = ρ(Ω2xdx + Ω2ydy – , (2-66)

что после интегрирования дает

dpA = ρ( + – ) + C = (x2 + y2) – ρ C. (2-67)

Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p0. Как видно,

C = p0 (2-68)

причем (2-67) перепишется в виде:

pA = p0 + (x2 +y2) – γz (2-69)

Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.

Действительно, уравнение поверхности, во всех точках которой давление pA = pi= const, запишется в виде

(x2 +y2) – γz = pi – p0. (2-70)

Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).

Свободная поверхность жидкости, характеризуемая постоянным давлением pi = p0, представляет собой также параболоид вращения; уравнение ее будет:

(x2 +y2) – γz = 0. (2-71)

Если учесть, что x2 + y2 = r2, то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:

z0 = r2 (2-72)

где z0- ордината кривой АОВ.

Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):

pA = p0 + (x2 +y2) +γa = p0 + ρ r2+ γa = p0 + γ( r2+ a). (2-73)

Учитывая (2-72), получаем

pA = p0 + γ(a + z0) = p0 + γh (2-74)

где h = a +z0 показано на рис. 2-14.

Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.

Источник

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.

Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.

Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.

Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил

(2.12)

определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения

tga = а/g.

Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость

p = p0 + l ρ j. (2.13)

Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.

Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики.

Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω2 r. Равнодействующая этих двух сил

определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением

где z0 — высота расположения точки свободной поверхности относительно дна сосуда;

h0 — высота жидкости на оси вращения.

Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:

. (2.14)

На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:

. (2.15)

Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Источник

Содержание:

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси.

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси

Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. В состоянии равновесия в движущемся сосуде жидкость движется вместе со всем контейнером. То есть, жидкость находится в относительном состоянии покоя. Рассмотрим цилиндрический контейнер радиусом H (рис. 2.9), заполненный до определенного уровня жидкостью плотностью p и вращающийся с постоянной угловой скоростью относительно вертикальной оси.

Через некоторое время после начала вращения сосуда жидкость под действием трения вращается с той же скоростью, что и сосуд. Равновесие жидкости устанавливается для сосуда, другими словами, для неинерциальных систем координат x, y, r, которые вращаются вместе с сосудом. При написании уравнений равновесия в неинерциальных системах необходимо ввести силу подвижной инерции в число рабочих forces.

В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести.
Людмила Фирмаль

В рассматриваемом случае такая сила направлена вдоль радиуса и равна & M (центробежная сила равна n2g элементарной массы AM, которая вращается на расстоянии r от вертикали axis. In помимо центробежной силы, гравитация DM ^действует на любую частицу AM-это: за счет силы тяжести ^ = ° ;=°; ПГХ = —§; От портативной инерции п *. =<sup class=»reg»>®</sup>ГХ Риш-0)2 в> пр%= 0、 Где*и y-горизонтальные координаты произвольно выбранной точки А в жидкости. Рассмотрим 2 вопроса здесь. 39.

Форма поверхности одинакового давления. Используйте уравнение поверхности равного давления (2.10)’ Rhyh + ру ю + Rghyg-0 Когда вы назначаете ему выражения Px, Py и Pr, вы находите co2 x yx + co2 yy-diig-0. После интеграции、 гг-(* 2 + У2) §Р= С Или Х2 + У2-Г2.、 СО2-Р2 / 2 §р= с(2.23） Как видно из (2.23), поверхность равного давления в этом случае представляет собой семейство совпадающих 1-вращающихся параболоидов с вертикальной осью. Различные значения константы C соответствуют различным параболам одинакового давления.

Свободная поверхность это также поверхность, на которой давление во всех точках равно давлению, равному внешнему давлению p0. Найти значение любой константы c параболоида свободной поверхности. Х-0; У = 0; РСВ = Р0.Если подставить эти координаты в Формулу (2.23), то: Ц0 = § 0. Уравнения свободной поверхности * С ш-Р0 = ^ (*2 +! 2. ） 2-й. Или Огнестрел-20 = СО2 Г2 / 2Д, (2.24） Частицы жидкости, находящиеся в относительном стационарном состоянии во вращающемся сосуде на расстоянии радиуса r от оси вращения, имеют линейную скорость u-(π.

Высота, на которой точка свободной поверхности выше вершины параболоида(например、 Б = РК-Р0 = СО2 Р2 /2§= С2 / 2С (2.25） 1 матч-фигура, которая будет объединена при наложении. 40. 20 ордината вершины параболоида свободной поверхности при заданной угловой скорости зависит от количества жидкости в сосуде. Если перед вращением сосуда уровень жидкости был установлен на горизонтальную и высоту H, то объем жидкости был равен 2N2H.

Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
Людмила Фирмаль

При вращении сосуда свободная поверхность становится параболой, форма объема жидкости изменяется, а величина при p = const{остается неизменной： | (Р0 +(r212d О2 ） О После интеграции、 Ч ■= рН + П2 К2 / 4Д Или Р0 = я-п * д * / 4#. Предполагая, что 20 = 0, мы знаем угловую скорость a, когда свободная поверхность жидкости касается дна контейнера. w = 2 Уды / я. Закон распределения давления. Используя дифференциальное уравнение жидкостных равновесий (2.5) и подставляя в него проекцию распределения плотности массовых сил, он выглядит следующим образом: гг = pY2(xc1x + ыыы) Сделай сам.

После интегрирования уравнения(2.26)、 / ? п(w2g72-ДГ)+ КБ(2.27） Если подставить координаты r = 0, r-r0 и давление p = p0 в уравнение (2.27), то получим Cp. С1! = Р0-Р (н0)= Р0 + rd0 Подставляя найденные значения C1 в(2.27), получаем 2r2 / 2d = H ’позволяет переписать любую точку в виде (2.28). Здесь k-глубина погружения точки под свободную поверхность, то есть вертикальное расстояние от свободной параболы до точки задачи. Поэтому в жидкости, которая неподвижна в равномерно вращающемся сосуде, вертикальное давление распределяется по закону гидростатического давления.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

Равновесие однородной несжимаемой жидкости относительно земли.
Геометрическая интерпретация основного уравнения гидростатики.
Силы давления покоящейся жидкости на горизонтальные и наклонные плоские площадки (стенки).
Силы давления покоящейся жидкости на цилиндрические стенки.

Источник

Цель работы

Исследование зависимости формы свободной поверхности жидкости от угловой скорости вращения цилиндрического сосуда относительно его вертикальной оси симметрии.

При выполнении работы необходимо:

• экспериментально определить z0 on и горизонтальные координаты точек кривой свободной поверхности жидкости, вращающейся вместе с сосудом с угловой скоростью
• теоретически определить z0Teop при значении взятом из опытов;
• сопоставить опытные и теоретические значения величин z0;
• сопоставить глубину параболоида вращения при двух различных угловых скоростях со
• построить теоретические и опытные кривые свободной поверхности равномерно вращающейся жидкости при двух различных угловых скоростях со
• определить частоту вращения сосуда со по известным из опыта координатам свободной поверхности z0on.

Описание опытной установки

Исследования проводятся на установке ГД-2, позволяющей экспериментально определить форму свободной поверхности жидкости во вращающемся сосуде (рис. 4.3). Установка состоит из корпуса (1), цилиндрического сосуда (2) радиусом г = 0,08 м, заполненного на 0,6 своей высоты маслом и приводимого во вращение через червячный редуктор электродвигателем, измерительной иглы (3), рукояти (4), шкал (5) и (6), размещенных на направляющей (7) рукояти (8), панели (9) с расположенными на ней тумблером и лампочкой (11), индикатора (12) для регистрации частоты вращения сосуда с жидкостью, регулятора частоты вращения (13).

Методика и порядок проведения испытаний

Поворотом тумблера (10) (рис. 4.3), расположенного на панели (9), включается электродвигатель и приводится во вращение сосуд (2) с жидкостью.

Вращением регулятора (13) устанавливается заданная частота вращения сосуда, величину установленной частоты вращения определяют по стрелочному счетчику оборотов (12).

Через 2-3 мин, т.е. после того как жидкость в сосуде придет в состояние относительного покоя (по отношению к стенкам вращающего сосуда), начинают производить измерения координат свободной поверхности жидкости. Для этого вращением рукояти (4) мерную иглу (3) устанавливают так, чтобы ось иглы совпадала с осью сосуда (отметка “0” на горизонтальной шкале). Затем вращением рукояти (3) измерительную иглу опускают до соприкосновения её острия со свободной поверхностью жидкости и производят отсчет по нониусу иглы. После этого иглу поднимают вверх и перемещают в горизонтальном направлении (влево или вправо от оси сосуда) на 1 см и снова опускают до соприкосновения её острия со свободной поверхностью, берут отсчет по нониусу с точностью до 0,1 мм.

Рис. 4.3. Схема опытной установки ГД-2:

1 – корпус; 2 – цилиндрический сосуд; 5 – измерительная игла;
4,8 – рукояти, 5,6 – шкалы; 7 – направляющая, 9 – панель; 10 – тумблер; 11 – лампочка; 12 – индикатор; 13 – регулятор; 14 – штанга

Аналогичные измерения проводят для ряда других точек, расположенных вдоль радиуса сосуда (7…8 точек).

Регулятором (13) изменяют частоту вращения сосуда с жидкостью и повторяют все измерения.

По окончании измерений необходимо выключить тумблер (10). Данные измерений заносят в табл. 4.1.

Таблица 4.1

Измерение координат свободной поверхности

№

ТОЧКИ

Отсчет по горизонтальной шкале, см

Отсчёт по вертикальной шкале, см

iii =

ГЬ =

п, =

ГЬ =

Обработки результатов измерений

С помощью экспериментально полученных данных вычисляют zoon при различных частотах вращения сосуда П и п2 относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности как разность отсчетов по вертикальной шкале, соответствующих данной точке свободной поверхности и положению иглы в центре сосуда.

По формуле (4.4) вычисляют теоретические значения z0Teop поверхности относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности, при этом берется гтеор = гоп.

Расхождение в процентах между величинами z0on и z(trcop подсчитывают по формуле

Результаты вычислений заносят в табл. 4.2.

Таблица 4.2

Определение отметок свободной поверхности

№ точки	Расстояние от точки до оси вращения г, м	Угловая скорость вращения сосуда to, рад/с	Отметки свободной поверхности, м				Расхождение между zoom и ^Отсор» /о
			Пэ =		Пэ =
			ZO on	ZO тсор	Z ом	Z() тсор
	П1 = Пэ =	и с И с					Пэ = П2 =

На графике в масштабе 1:2 строят теоретические и экспериментальные кривые свободной поверхности жидкости z0on= f(r) и z() теор = f(r), используя карандаши различного цвета.

По формуле (4.4) и величине z0on третьей серии измерений вычисляют угловую скорость вращения сосуда со, а затем из зависимости

вычисляют частоту вращения п сосуда с жидкостью.

1. Какие силы действуют на жидкость при абсолютном покое?
2. Какие силы действуют на жидкость в случае её относительного покоя?
3. Какую форму принимает свободная поверхность жидкости в случае абсолютного и относительного покоя жидкости?
4. Как определить глубину параболоида вращения?
5. От чего зависит глубина параболоида вращения?
6. Каково уравнение поверхности равного давления в случае абсолютного и относительного покоя жидкости?
7. Запишите уравнение равновесия жидкости для абсолютного и относительного покоя (уравнение Эйлера) и объясните смысл входящих в него величин.
8. Запишите уравнение свободной поверхности жидкости для случая равномерного вращения цилиндрического сосуда вокруг собственной вертикальной оси?
9. Как определить угловую скорость вращения сосуда?

Источник