Периферическое сопротивление сосудов по пуазейлю
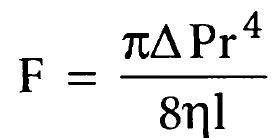
Закон Пуазейля. Диаметр артериол и их сопротивлениеПричину такого значительного возрастания объемного кровотока при увеличении диаметра сосуда можно объяснить с помощью схемы, представленной на рисунке. На схеме показано поперечное сечение крупного и мелкого кровеносных сосудов. Концентрические слои внутри сосудов указывают на то, что скорость движения каждого слоя отличается от скорости соседних слоев, т.к. происходит ламинарное течение крови (см. ранее в данной главе). Дело в том, что слой крови, прилежащий к стенке сосуда, едва движется благодаря взаимодействию крови и эндотелия сосудистой стенки. Следующий слой крови скользит относительно пристеночного слоя и поэтому движется быстрее. Третий, четвертый, пятый и шестой слои также текут с нарастающей скоростью. Таким образом, пристеночный слой крови движется чрезвычайно медленно, в то время как по продольной оси сосуда кровь движется с наибольшей скоростью. В мелких сосудах практически вся кровь оказывается вблизи сосудистой стенки, поэтому быстротекущего центрального потока крови просто не существует. Сложив скорости всех концентрических слоев текущей крови, умноженные на площади поперечного сечения каждого слоя, можно вывести формулу, известную как закон Пуазейля:
где F — скорость кровотока, АР — разница давления на концах сосуда, r — радиус сосуда, 1 — длина сосуда и n — вязкость крови. Обратите внимание, что в этом уравнении скорость кровотока прямо пропорциональна четвертой степени радиуса сосуда. Это еще раз показывает, что среди всех факторов, определяющих скорость кровотока, диаметр кровеносного сосуда, равный двум радиусам, имеет первостепенное значение. Влияние диаметра артериол на их сопротивление (закон четвертой степени). В большом круге кровообращения почти 2/3 общего периферического сопротивления приходится на мелкие артериолы. Внутренний диаметр артериол имеет величину от 4 до 25 мкм. Однако мощная мышечная стенка артериол позволяет существенно менять внутренний диаметр, часто более чем в 4 раза. Исходя из закона четвертой степени, который определяет зависимость объемного кровотока от диаметра сосудов, четырехкратное увеличение диаметра приводит к возрастанию объемного кровотока, по меньшей мере, в 256 раз. Таким образом, незначительные изменения диаметра артериол в ответ на нервные сигналы или действие местных гуморальных факторов может привести или к почти полному прекращению кровотока в тканях, или — в других экстремальных ситуациях — резко увеличить кровоток. И действительно, в отдельных сосудистых областях регистрируется увеличение местного кровотока в 100 раз при переходе артериол из состояния максимального сужения к состоянию их максимального расширения. Сопротивление сосудов, соединенных между собой последовательно и параллельно. Кровь, которая поступает в большой круг кровообращения из сердца, движется из области с высоким давлением (аорта) в область с низким давлением крови (полые вены). Кровь течет через обширную сосудистую сеть, в которой многочисленные сосуды соединены между собой последовательно и параллельно. Артерии, артериолы, капилляры, венулы и вены в целом являются системой последовательно соединенных сосудов. Общее сопротивление такой системы представляет собой сумму сопротивлений каждого отдельного сосуда:
Следовательно, общее периферическое сопротивление равно сумме сопротивлений артерий, артериол, капилляров, венул и вен. На примере, приведенном на рисунке, общее сосудистое сопротивление равно сумме сопротивлений R1 и R2. Благодаря разветвлению сосудов формируются параллельные сосудистые сети, снабжающие кровью многочисленные органы и ткани организма. Формирование параллельных сосудистых сетей позволяет каждому органу и даже участку органа в большой степени регулировать собственный местный кровоток независимо от других органов и тканей. Очевидно, что при одном и том же градиенте давления гораздо больший объем крови будет протекать через систему параллельных сосудов, чем через любой отдельно взятый сосуд. Таким образом, общее сопротивление системы параллельных сосудов оказывается гораздо меньше, чем сопротивление любого отдельного сосуда. Кровоток через каждый из параллельных сосудов на рисунке зависит от градиента давления и сопротивления данного сосуда, а не сопротивления всей системы. Однако увеличение сопротивления одного из сосудов параллельной системы приведет к увеличению сопротивления всей системы. Кажется парадоксальным, что дополнительное увеличение количества сосудов в параллельной системе приводит к уменьшению общего сосудистого сопротивления. Дело в том, что множество параллельных сосудов облегчает протекание крови через сосудистую сеть, т.к. каждый параллельный сосуд обеспечивает дополнительный путь кровотоку, увеличивая так называемую проводимость системы для крови. Итак, общая проводимость системы параллельных сосудов (Собщая) представляет собой сумму проводимостей каждого отдельного сосуда: Собщее = С1+С2+С3+С4…. Например, сосуды головного мозга, почек, мышц, желудочно-кишечного тракта, кожи, сердца представляют собой отдельные, параллельно соединенные системы, каждая из которых вносит свой вклад в общую проводимость большого круга кровообращения. Объемный кровоток каждого органа является частью общего кровотока (сердечного выброса) и зависит от сопротивления кровотоку (или проводимости) органа так же, как и от градиента давления. Следовательно, ампутация конечности или хирургическое удаление почки приводит к удалению одной из параллельных сосудистых систем большого круга кровообращения и уменьшает общую сосудистую проводимость и объемный кровоток (т.е. сердечный выброс), в то время как общее периферическое сопротивление увеличивается. – Вернуться в оглавление раздела “Физиология человека.” Оглавление темы “Сосудистая система”: |
Источник
Сопротивляемость сосудов. Проводимость сосудов
Сопротивление представляет собой препятствие кровотоку, которое возникает в кровеносных сосудах. Сопротивление не может быть измерено никаким прямым методом. Оно может быть рассчитано с использованием данных о величине кровотока и разницы давления на обоих концах кровеносного сосуда. Если разница давления равна 1 мм рт. ст., а объемный кровоток равен 1 мл/сек, сопротивление составляет 1 единицу периферического сопротивления (ЕПС).
Сопротивление, выраженное в единицах системы СГС. Иногда для выражения единиц периферического сопротивления используют единицы системы СГС (сантиметры, граммы, секунды). В этом случае единицей сопротивления будет дина сек/см5.
Общее периферическое сосудистое сопротивление и общее легочное сосудистое сопротивление. Объемная скорость кровотока в системе кровообращения соответствует сердечному выбросу, т.е. тому объему крови, которое сердце перекачивает за единицу времени. У взрослого человека это составляет примерно 100 мл/сек. Разница давления между системными артериями и системными венами равна примерно 100 мм рт. ст. Следовательно, сопротивление всего системного (большого) круга кровообращения или, иными словами, общее периферическое сопротивление соответствует 100/100 или 1 ЕПС.
В условиях, когда все кровеносные сосуды организма резко сужены, общее периферическое сопротивление может возрасти до 4 ЕПС. И наоборот, если все сосуды окажутся расширенными, сопротивление может упасть до 0,2 ЕПС.
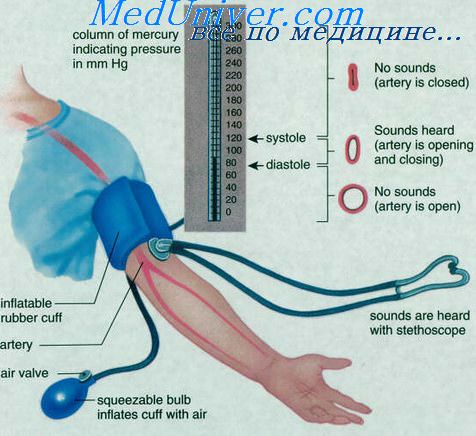
В сосудистой системе легких артериальное давление в среднем равно 16 мм рт. ст., а среднее давление в левом предсердии — 2 мм рт. ст. Следовательно, общее легочное сосудистое сопротивление составит 0,14 ЕПС (примерно 1/7 общего периферического сопротивления) при обычном сердечном выбросе, равном 100 мл/сек.
Проводимость сосудистой системы для крови и ее взаимосвязь с сопротивлением. Проводимость определяется объемом крови, протекающим по сосудам, за счет данной разницы давления. Проводимость выражается в миллилитрах за секунду на миллиметр ртутного столба, но может быть выражена также в литрах за секунду на миллиметр ртутного столба или в каких-либо других единицах объемного кровотока и давления.
Очевидно, что проводимость — это величина, обратная сопротивлению: проводимость=1/сопротивление.
Незначительные изменения диаметра сосудов могут привести к существенным изменениям их проводимоаи. В условиях ламинарного течения крови незначительные изменения диаметра сосудов могут резко изменить величину объемного кровотока (или проводимость кровеносных сосудов). На рисунке показаны три сосуда, диаметры которых соотносятся как 1, 2 и 4, а разница давления между концами каждого сосуда одинакова — 100 мм рт. ст. Скорость объемного кровотока в сосудах равна 1, 16 и 256 мл/мин, соответственно.
Обратите внимание, что при увеличении диаметра сосуда только в 4 раза объемный кровоток увеличился в нем в 256 раз. Таким образом, проводимость сосуда увеличивается пропорционально четвертой степени диаметра в соответствии с формулой: Проводимость ~ Диаметр.
– Также рекомендуем “Закон Пуазейля. Диаметр артериол и их сопротивление”
Оглавление темы “Сосудистая система”:
1. Электрокардиограмма при фибрилляции желудочков. Электрошоковая дефибрилляция желудочков
2. Ручной массаж сердца в помощь дефибрилляции. Фибрилляция предсердий
3. Трепетание предсердий. Остановка сердца
4. Функциональные участки системы кровообращения. Объемы крови в различных отделах сосудистой системы
5. Давление крови в различных участках сосудистой системы. Теоретические основы кровообращения
6. Регуляция объема кровотока и периферического сопротивления. Объемный кровоток
7. Ультразвуковой флоуметр. Ламинарное течение крови в сосудах
8. Турбулентное течение крови. Давление крови
9. Сопротивляемость сосудов. Проводимость сосудов
10. Закон Пуазейля. Диаметр артериол и их сопротивление
Источник
Зако́н Пуазёйля (иногда закон Га́гена — Пуазёйля или в иной транскрипции — закон Ха́гена — Пуазёйля) — физический закон гидродинамики для так называемого течения Пуазёйля, то есть установившегося течения вязкой, в частном случае несжимаемой, жидкости в тонкой цилиндрической трубе. Связывает расход жидкости через сечение трубы с перепадом давления на концах её при заданных вязкости жидкости и геометрических размерах трубки.
Закон установлен эмпирически в 1839 году Г. Хагеном, а в 1840—1841 годах — независимо от него Ж. Л. Пуазёйлем. Теоретически объяснён Дж. Г. Стоксом в 1845 году.
Формулировка закона[править | править код]
При установившемся ламинарном течении вязкой несжимаемой жидкости сквозь длинную (то есть при длине трубы многократно превышающей её диаметр) прямую цилиндрическую трубу (капилляр) круглого сечения объёмный расход жидкости прямо пропорционален перепаду давления на единицу длины трубы и четвёртой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.
где
Формула справедлива, во-первых, если течение жидкости ламинарное, и, во-вторых, ламинарное течение установившееся, профиль скоростей в котором описывается течением Пуазёйля, когда можно пренебречь влиянием концов трубы.
Явление, описываемое формулой, иногда используется для экспериментального определения вязкости жидкостей. Другим способом определения вязкости жидкости является метод, использующий закон Стокса.
Закон Пуазёйля для течения сжимаемой жидкости в трубе[править | править код]
Для сжимаемой жидкости в трубе (газа), объёмный расход и линейная скорость не постоянны вдоль трубы, при больших давлениях скорость и объемный расход меньше при неизменном расходе газа, приведённого к нормальным условиям. Поскольку газ при течении расширяется, то в общем случае температура газа изменяется вдоль трубы, то есть процесс неизотермический.
Это означает, что скорость потока зависит не только от давления в данном сечении трубы, но и от температуры газа.
Для идеального газа в изотермическом случае, когда температура газа за счёт теплообмена со стенкой трубы успевает выравняться с температурой стенки и когда разность давлений между концами трубы мала относительно среднего давления вдоль трубы, объёмный расход на выходе из трубы определяется выражением:
где — входное давление, Па;
— выходное давление, Па;
— длина трубы, м;
— динамическая вязкость, Па·с;
— радиус, м;
— объёмный расход газа при выходном давлении, м3/с.
Это уравнение можно рассматривать как закон Пуазёйля с дополнительным коэффициентом для усреднения давления вдоль трубы:
Вариации и обобщение[править | править код]
Имеется обобщение формулы закона Пуазёйля для длинной трубы эллиптического сечения. Из формулы для трубы эллиптического сечения следует формула закона Пуазейля для течения жидкости между двумя параллельными плоскостями (в предельном случае, когда большая полуось эллипса стремится к бесконечности). В справочной литературе приведены формулы для профиля скоростей потока жидкости и для расхода жидкости через единицу площади[1][2].
Примечания[править | править код]
Литература[править | править код]
- Вишневецкий С. М. Пуазёйля Закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
- Sutera S.P., Skalak R. The history of Poiseuille’s law // Annual review of fluid mechanics. — 1993. — Т. 25. — С. 1–19.
- Эберт Г. Краткий справочник по физике: справочное издание / под ред. К. П. Яковлева. — пер. со 2-го нем. изд. Н. М. Шикуниной. — М. : Физматгиз, 1963. — 552 с.
- Яворский Б. М., Детлаф А. А. Справочник по физике. — Наука, 1978. — 944 с.
Ссылки[править | править код]
- Оригинальные публикации Хагена и Пуазёйля
Источник
Оглавление темы “Функции систем кровообращения и лимфообращения. Система кровообращения. Системная гемодинамика. Сердечный выброс.”:
1. Функции систем кровообращения и лимфообращения. Система кровообращения. Центральное венозное давление.
2. Классификация системы кровообращения. Функциональные классификации системы кровообращения ( Фолкова, Ткаченко).
3. Характеристика движения крови по сосудам. Гидродинамические характеристики сосудистого русла. Линейная скорость кровотока. Что такое сердечный выброс?
4. Давление кровотока. Скорость кровотока. Схема сердечно-сосудистой системы ( ССС ).
5. Системная гемодинамика. Параметры гемодинамики. Системное артериальное давление. Систолическое, диастолическое давление. Среднее давление. Пульсовое давление.
6. Общее периферическое сопротивление сосудов ( ОПСС ). Уравнение Франка.
7. Сердечный выброс. Минутный объем кровообращения. Сердечный индекс. Систолический объем крови. Резервный объем крови.
8. Частота сердечных сокращений ( пульс ). Работа сердца.
9. Сократимость. Сократимость сердца. Сократимость миокарда. Автоматизм миокарда. Проводимость миокарда.
10. Мембранная природа автоматии сердца. Водитель ритма. Пейсмекер. Проводимость миокарда. Истинный водитель ритма. Латентный водитель ритма.
Общее периферическое сопротивление сосудов ( ОПСС ). Уравнение Франка.
Под этим термином понимают общее сопротивление всей сосудистой системы выбрасываемому сердцем потоку крови. Это соотношение описывается уравнением:
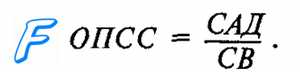
Как следует из этого уравнения, для расчета ОПСС необходимо определить величину системного артериального давления и сердечного выброса.
Прямых бескровных методов измерения общего периферического сопротивления не разработано, и его величина определяется из уравнения Пуазейля для гидродинамики:
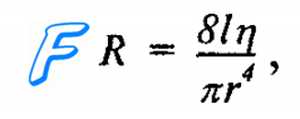
где R — гидравлическое сопротивление, l — длина сосуда, v — вязкость крови, r — радиус сосудов.
Поскольку при исследовании сосудистой системы животного или человека радиус сосудов, их длина и вязкость крови остаются обычно неизвестными, Франк, используя формальную аналогию между гидравлической и электрической цепями, привел уравнение Пуазейля к следующему виду:
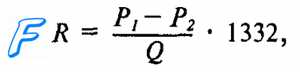
где Р1—Р2 — разность давлений в начале и в конце участка сосудистой системы, Q — величина кровотока через этот участок, 1332— коэффициент перевода единиц сопротивления в систему CGS.
Уравнение Франка широко используется на практике для определения сопротивления сосудов, хотя оно не всегда отражает истинные физиологические взаимоотношения между объемным кровотоком, АД и сопротивлением сосудов кровотоку у теплокровных. Эти три параметра системы действительно связаны приведенным соотношением, но у разных объектов, в разных гемодинамических ситуациях и в разное время их изменения могут быть в разной мере взаимозависимыми. Так, в конкретных случаях уровень САД может определяться преимущественно величиной ОПСС или в основном СВ.
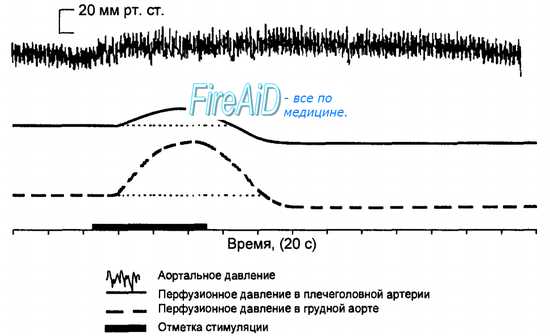
Рис. 9.3. Более выраженная величина повышения сопротивления сосудов бассейна грудной аорты по сравнению с его изменениями в бассейне плечеголовной артерии при прессорном рефлексе.
В обычных физиологических условиях ОПСС составляет от 1200 до 1700 дин • с ¦ см , при гипертонической болезни эта величина может возрастать в два раза против нормы и быть равной 2200—3000 дин • с • см-5.
Величина ОПСС состоит из сумм (не арифметических) сопротивлений регионарных сосудистых отделов. При этом в зависимости от большей или меньшей выраженности изменений регионарного сопротивления сосудов в них соответственно будет поступать меньший или больший объем крови, выбрасываемый сердцем. На рис. 9.3 показан пример более выраженной степени повышения сопротивления сосудов бассейна нисходящей грудной аорты по сравнению с его изменениями в плечеголовной артерии. Поэтому прирост кровотока в плечеголовной артерии будет больше, чем в грудной аорте. На этом механизме базируется эффект «централизации» кровообращения у теплокровных, обеспечивающий в тяжелых или угрожающих организму условиях (шок, кровопотеря и др.) перераспределение крови, прежде всего, к головному мозгу и миокарду.
– Также рекомендуем “Сердечный выброс. Минутный объем кровообращения. Сердечный индекс. Систолический объем крови. Резервный объем крови.”
Источник

