Первый сосуд содержит 30 кг а второй 20 кг

4 февраля 2014

Итак, сегодня мы пошагово разберем довольно сложную задачу на смеси и сплавы, которая в итоге сведется к системе из двух уравнений. После просмотра этого видео вы будете щелкать эти задачи как орешки — потому что на самом деле они не такие уж и сложные.:)

Сегодня мы продолжаем рассматривать текстовые задачи из ЕГЭ по математике и на очереди у нас задача про смеси и сплавы. Обычно я решаю такие задачи про смеси и сплавы с помощью таблиц, подобно примерам на движение и производительность труда. Однако недавно с учениками мы опробовали новый, более наглядный способ решения, который оказался быстрее, чем способ решения с помощью таблиц, но самое главное — он оказался таким же правильным и понятным, как и классические приемы. Давайте попробуем.

Задача:

Имеются два сосуда. Первый содержит 30 кг, а второй — 20кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится смесь, содержащая 70% кислоты. Сколько килограммов чистой кислоты содержится в первом сосуде?

Давайте переведем это условие на язык математики. У нас есть сосуд, который содержит 30 кг кислоты. Концентрацию ее мы не знаем, поэтому давайте обозначим ее за xx. В этом случае в нашем сосуде чистого вещества будет 30x100frac{30x}{100}:

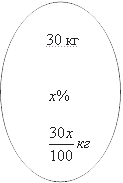
Теперь переходим ко второму сосуду. В нем имеется 20 кг раствора этого же вещества, но его концентрация опять же неизвестна, поэтому обозначим ее за yy%. В этом случае масса чистого вещества в сосуде равна 20y100frac{20y}{100}:

А теперь согласно условию мы смешиваем эти растворы и получаем новый со следующими параметрами. Разумеется, масса новой смеси будет равна сумме масс исходных смесей, т. е. 20+30=5020+30=50. При этом mm чистой кислоты при смешивании также складываются. А это значит что ее масса в новом веществе равна:

30100+20y100

frac{30}{100}+frac{20y}{100}

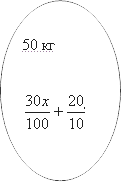
Но с другой стороны, эта же смесь может быть описана следующими цифрами. Ееmm все также составляет 50 кг, а вот концентрация — 68%. Это прямо указано в условии задачи. Следовательно, масса кислоты может быть найдена следующим образом:

50⋅68100

50cdot frac{68}{100}

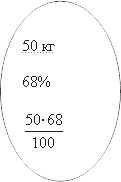
А поскольку в обеих кружках описан один и тот же раствор, мы можем первое выражение приравнять ко второму. Мы получим следующее уравнение:

30×100+20y100=50⋅68100

frac{30x}{100}+frac{20y}{100}=frac{50cdot text{68}}{text{100}}

3x−2y=5⋅68

3x-2y=5cdot 68

3x+2y=340

3x+2y=340

Итак, мы получили первое уравнение задачи на смеси и сплавы. Возвращаемся к условию задачи про смеси и сплавы и читаем дальше: если же смешать равные массы этих растворов, то получится вещество, содержащее 70% кислоты.

Давайте чертить новые кружки. У нас есть два раствора, но теперь их масса не 30 и 20 кг, а равная, скажем, по 10 кг. Разумеется, при решении других задач про смеси и сплавы мы вправе взять любое число, не только 10. Ответ при этом не изменится.

Итак, первая смесь. Ее mm 10 кг, а концентрация xx%. Это означает, что чистой кислоты в ней 10100frac{10}{100}:

Для второго примера, концентрация которого составляет yy%, mm составит 10 кг, а чистой кислоты 10y100frac{10y}{100}:

Теперь мы смешиваем их и получаем новый. При этом их массы тоже складываются:

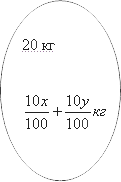
С другой стороны этот же раствор можно описать следующими цифрами: у нас есть 20 кг, а его концентрация по условию должна быть равна 70%. Следовательно, масса чистого вещества может быть найдена следующим образом:

20⋅70

20cdot 70

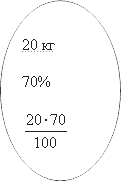
Поскольку данные в двух последних кружках равны, то мы можем записать следующее уравнение:

10×100+10y100=20 ⋅ 70100

frac{10x}{100}+frac{10y}{100}=frac{text{20 }!!cdot!!text{ 70}}{text{100}}

x+y=140

x+y=140

Итак, мы получили второе уравнение, которое вместе с первым образует систему:

{3x + 2y = 340x+y=140}

left{ left. begin{align}& text{3x }+text{ 2y }=text{ 340} \& text{x}+text{y}=text{140} \end{align} right} right.

Сейчас мы и будем ее решать. Давайте сначала выпишем эту систему.

Второе уравнение в нашей системе симметрично относительно переменных xx и yy, т. е. мы можем одинаковыми усилиями выразить и x и y. Так какую же переменную выражать? Для того, чтобы понять, какая из них оптимальная, давайте вернемся обратно к задаче и прочитаем вопрос: сколько килограммов чистого вещества содержится в первом сосуде? Именно первый сосуд. Концентрация, как мы помним, равна xx%. Следовательно, при решении этой системы уравнений задачи на смеси и сплавы нас, в первую очередь, интересует х. А это значит, что именно через xx мы должны выразить все, что у нас есть, в данном случае у. Этот прием используется во всех более-менее сложных задачах на смеси и сплавы.

При решении системы уравнений мы стараемся выразить не ту переменную, которая первой попадется нам на глаза, а ту, от которой нужно избавиться, чтобы получить одно уравнение с одной переменной, решение которой даст нам непосредственно ответ к задаче. Такой переменной у нас является xx, потому что зная xx, мы сразу найдем массу чистого вещества в первом сосуде, что от нас и требуется. А это значит, что через xx мы выражаем все остальное, в данном случае у. Давайте подставим:

{3x+2y=340x+y=140}

left{ left. begin{align}& text{3}x+text{2}y=text{340} \& x+y=text{140} \end{align} right} right.

{3x+2(140−x)=340y=140−x}

left. left{ begin{align}& 3x+2(140-x)=340 \& y=140-x \end{align} right. right}

3x+2(140−x)=340

3x+2(140-x)=340

3x+280−2x=340

3x+280-2x=340

x=60

x=60

Итак, мы нашли концентрацию чистого вещества в первом растворе. Она составляет 60%. Давайте подставим это число в выражение чистой mm, т. е.

30⋅60100=3⋅6=18

30cdot frac{60}{100}=3cdot 6=18

Вот и все, мы получили ответ — 18 кг. Именно столько чистого вещества содержится в первом сосуде.

Ключевые моменты

Давайте еще раз быстренько пробежимся по всем ключевым этапам решения этой задачи на смеси и сплавы. В первую очередь необходимо понять, что это за выражения стоять внизу кружочков, которые означают наши растворы. На самом деле все очень просто. Если есть некий раствор массой MM, в котором известно, что xx% этого раствора составляет кислота, то ее MM будет выражаться по формуле:

M⋅x100

Mcdot frac{x}{100}

Эту формулу легко запомнить, если понять, что M100frac{M}{100} — это 1% от MM исходного вещества.

Записывая таким образом массы чистой кислоты для каждого из веществ, а также для вещества, которое получается для смешивания, мы легко составим уравнение. Для этого нужно понимать, что при смешивании mm не меняется. Именно поэтому мы складываем $M$ кислоты в исходных веществах и приравниваем их к массе чистой кислоты в исходном веществе.

А дальше все просто. У нас получается да линейных уравнения, которые легко объединяются в систему, а затем решаются. Единственный момент, который возникает при решении таких систем состоит в том, что нужно выбрать самое простое уравнение и выразить их него не ту переменную, которую мы ищем для ответа на вопрос задачи, а как раз таки все остальное. Другими словами мы берем искомую переменную и через нее выражаем все остальные переменные, которые имеются в задаче.

В нашем случае такая переменная всего одна. Мы выражаем у через xx. А дальше мы получаем одно единственное уравнение относительно той самой переменной, которую мы ищем. Следовательно, всю систему вообще можно отбросить. Такое уравнение обычно легко решается.

Самое главное здесь — не забыть, что же конкретно мы ищем. А ищем мы вовсе не концентрацию исходной кислоты в процентах, а именно массу этой кислоты. Т. е. полученное выражение xx нужно еще подставить в выражение для чистой массы. Сделав это, посчитав полученную дробь, мы получим ответ. В нашем случае он составил 18 кг.

Интересные факты

В дополнение к видео хотел бы добавить, что по моим наблюдениям все ученики делятся на два типа:

1. Те, кто хорошо решает задачи на движение, но «зависает» на смесях и сплавах;
2. А также те, для кого смеси и сплавы — не проблема, а вот задачи на движение даются им с трудом.

Если вы относитесь ко второму типу учеников, не переживайте: таких людей около 40%, т.е. очень много. На самом деле задачи на движение и на смеси и сплавы имеют примерно одинаковый уровень педагогической сложности, однако при этом требуют разных навыков для быстрого решения. У кого-то эти навыки есть, а у кого-то — нет. Но если немного потренироваться, то оба типа задач окажутся вполне решаемыми.

Вот и все решение. Если немного потренироваться, то задачи на смеси и сплавы окажутся не такими уж и сложными.

Смотрите также:

1. Смеси и сплавы в задаче B14: неизвестна масса
2. Простая задача B14 на смеси и сплавы
3. Умножение и деление дробей
4. Задачи B12, сводящиеся к линейным уравнениям
5. C2: расстояние между двумя прямыми
6. Нестандартная задача B2: студенты, гонорары и налоги