Плавание тел плавание сосудов

Закон Архимеда

Местоположение предмета в пространстве объясняется действующими на него силами. Нарушение баланса приложенных усилий выводит объект из равновесного состояния и даёт старт движению. В газообразной среде и жидкости вертикальный ход тела зависит от пары сил — выталкивающей и тяжести. Закон, описывающий взаимодействие двух основных составляющих, открыл Архимед за три столетия до Рождества Христова.
Физик, математик, инженер
Архимед родился в 287 году до н. э. на Сицилии в греческой колонии Сиракузы. В детстве за воспитание мальчика взялся отец — астроном и математик Фидий. Всестороннее образование юноша получил в Александрии, где занимался изучением трудов Демокрита и Евдокса, общался с Эратосфеном и Кононом. Жизнь в научной столице древнего мира сформировала Архимеда как талантливого исследователя и экспериментатора.
Учёные, повлиявшие на образование Архимеда:
- греческий филолог и географ Эратосфен — вычислил размеры Земли;
- математик и астроном Конон, составлявший прогнозы погоды и календари с указанием времени восхода и заката Солнца;
- в трудах мыслителя Демокрита разработана теория неделимой частицы — атома, которая легла в основу материалистической философии;
- малоазиатский философ Евдокс, которого считают родоначальником интегральных вычислений и теоретической астрономии.
После обучения в Египте Архимед вернулся в Сиракузы, где жил до трагической гибели в 212 году до н. э. За три года до этого римляне начали осаду сицилийского города, который помогал Карфагенскому государству. Инженерный талант греческого математика помогал горожанам сдерживать нападавшие легионы. Осаждённые греки использовали катапульты разного калибра и подъёмные краны, которые при помощи крюков переворачивали вражеские галеры. Кривые зеркала, фокусирующие лучи в одну точку, сжигали неприятельский флот.
Существует несколько вариантов легенды о гибели Архимеда. Но описания совпадают в одном — мыслителя, занятого в этот момент научными изысканиями, убил римский солдат, после того как Сиракузы сдались на милость победителя.
Архимед написал тринадцать трактатов. В книгах учёного определены основные положения гидростатики и теоретической механики. Рассчитывая площади поверхности фигур и объёмы тел, математик заложил основы интегрального и дифференциального вычисления величин. Инженерные разработки великого изобретателя находят применение и в современных конструкциях.
Тело, погружённое в жидкость
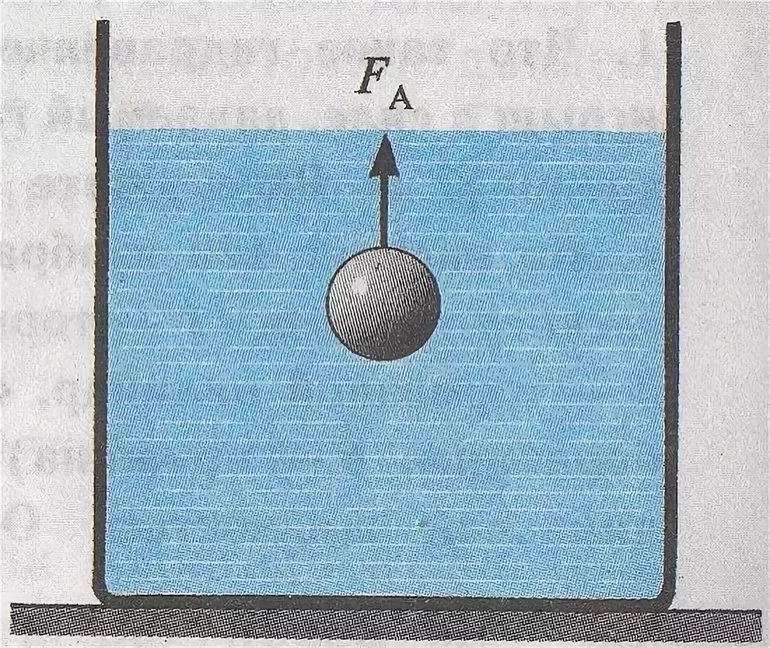
В истории науки известны примеры, когда практические запросы общества приводят к научным открытиям. Подобным образом был открыт основной закон статики. Вычисляя объём царской короны, Архимед погружал символ государственной власти в сосуд с водой. При этом учёный обратил внимание, что предмет, опущенный в жидкость, становится легче. Последующие размышления приводят великого грека к открытию гидростатического закона, названным его именем.
Закон Архимеда гласит, что на тело, погружённое в газовую среду или жидкость, действует сила, равная весу того объёма газа или жидкости, который вытеснило это тело. На языке математики постулат выражается уравнением:
F = gρV.
Смысловое определение математических символов, использованных в формуле:
- F — выталкивающая или архимедова сила;
- g — коэффициент ускорения свободного падения, равный 9,8 м/с²;
- ρ — плотность среды, в которую помещено тело;
- V — объём вытесненной жидкости или газа.
Архимедова сила противоположна силе тяжести и всегда направлена от центра Земли строго по вертикали вверх. В невесомости, где g = 0, закон Архимеда не работает. Взаимодействие двух сил — тяжести Ft и выталкивающей Fa — определяет поведение объекта в пространстве. Наглядным примером проявления силы Архимеда является подъём пузырька воздуха к поверхности воды.
На тело, плавающее на границе сред с разными плотностями, действует суммарная сила:
Fa = (ρ₁V₁ + ρ₂V₂ + ρ₃V₃ +…),
где ρ₁, ρ₂, ρ₃ – плотности различных сред, а V₁, V₂, V₃ – объёмы частей предмета.
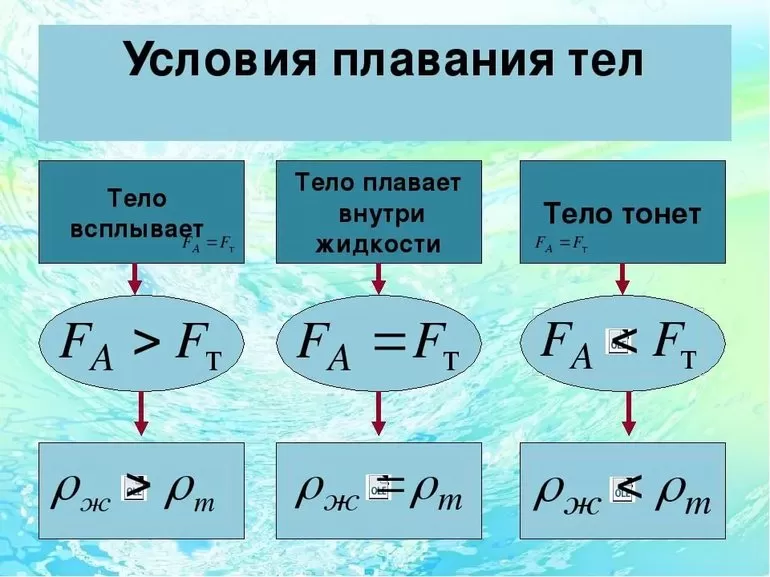
Разбирают три варианта развития событий:
- Если Ft ˂ Fa, то тело начинает всплывать.
- При условии Ft = Fa, объект пребывает в состоянии покоя.
- Если Ft ˃ Fa, то происходит погружение предмета.
Аналогичным образом развивается ситуация, если значения сил заменить величинами плотностей тела и жидкости или газа. То есть, вместо силы тяжести Ft использовать плотность предмета, а взамен выталкивающей силы Fa рассматривать плотность среды, в которую помещён объект.
Корабли не тонут, дирижабли летают
Плавучестью корабля называется способность судна оставаться в равновесном состоянии, не всплывая и не погружаясь на глубину. По закону Архимеда условия плавания тел возникают при равенстве силы тяжести выталкивающей силе. Запас плавучести определяется процентным отношением объёма водонепроницаемой полости выше ватерлинии к объёму всего корабля. Надводные суда рассчитываются с резервом плавучести не менее 50%.
Формула расчёта запаса плавучести:
W = v / V * 100%,
где W — запас плавучести, v — объём отсеков над ватерлинией, V — объём всего корабля.
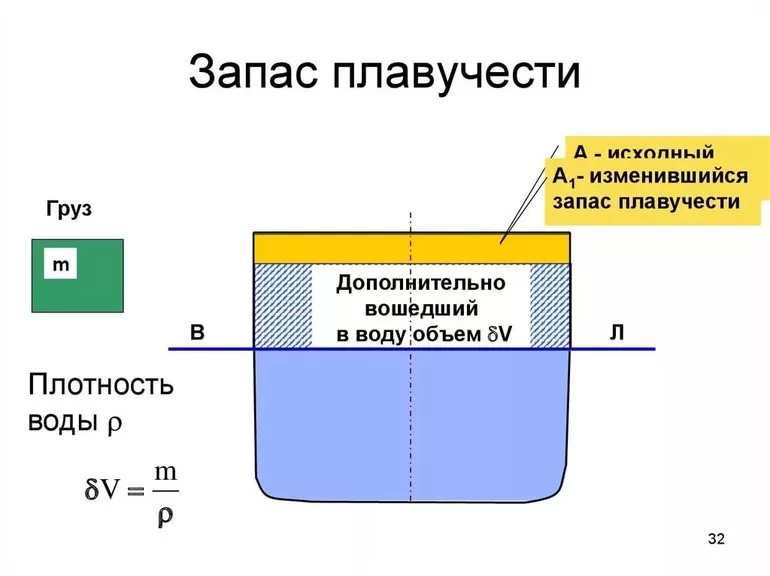
Водоизмещение является основной характеристикой водного транспорта и равно количеству воды, вытесненной подводной частью плавательного средства. Ватерлиния, являясь горизонтальным сечением, обозначается на корпусе и визуально показывает уровень нормального водоизмещения. Вычитание веса судна из водоизмещения представит грузоподъёмность транспортного средства.
В физическом смысле запас плавучести обозначает возможность находиться на поверхности водоёма. Различают нейтральную и отрицательную плавучесть. В первом случае W = 0% и судно погружено в воду до уровня палубы. Малейшее внешнее воздействие приводит к затоплению. Во втором случае корабль не способен держаться на плаву.
Предмет, находящийся в воздухе, также испытывает влияние архимедовой силы. Если подъёмная сила превышает силу тяжести, то тело начинает удаляться от поверхности земли. На этом постулате основан принцип воздухоплавания. В формуле закона Архимеда используется плотность воздуха.
Чтобы летательный аппарат поднялся, оболочку аэростата или дирижабля наполняют газом легче воздуха. Для этого подходят водород и гелий, чьи плотности меньше смеси атмосферных газов. Из-за взрывоопасности водорода чаще применяется гелий.
Идеальным вариантом считается использование в оболочке воздушного шара подогретого воздуха. Горелка устанавливается под отверстием в нижней части сферы. Периодическое включение нагревательного элемента изменяет температуру и плотность воздуха внутри шара, что позволяет регулировать скорость подъёма или спуска.
Решение примеров

Задача 1. Необходимо вычислить выталкивающую силу воды, действующую на сплошное тело цилиндрической формы объёмом 2 м³. Табличное значение плотности воды равно 1 тыс. кг/м³.
Решение. Прежде всего, определяется масса вытесненной воды:
m = ρ * V = 1000 * 2 = 2 тыс. кг.
Вес вытесненной воды, то есть архимедова сила, равны:
P = Fa = g * m = 9,8 * 2000 = 19600 Н.
Задача 2. Требуется определить количество золота в короне, изготовленной из сплава серебра и золота. Вес изделия в воздухе — 2,54 кг. Взвешивание в воде показало результат 2,34 кг.
Решение. На предмет, погружённый в воду, действует архимедова сила:
Fa = gρV = P₁ – P₂,
где P₁ – вес короны в воздухе, P₂ – вес драгоценности в воде, ρ — плотность воды.
Общий объём предмета складывается из объёмов золота и серебра:
V = m₁/ρ₁ + m₂/ρ₂,
где m₁ и ρ₁ – соответственно масса и плотность золота, а m₂ и ρ₂ – масса и плотность серебра.
Поскольку масса является частным от деления веса на коэффициент g, то общий объём короны можно представить формулой:
V = m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁),
где выражение (P₁/g — m₁) = m₂.

Значение объёма V подставляется в уравнение закона Архимеда:
Fa = g * ρ * (m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁)) = P₁ – P₂.
Путём математических преобразований определяется m₁:
m₁ = (P₁* (1 — ρ/ρ₂) — P₂)/(g * ρ * (1/ρ₁ – 1/ρ₂)).
Подставив числовые значения коэффициентов и веса короны, получаем ответ: m₁ = 985 г
О существовании трактатов Архимеда европейцам стало известно в XII веке. В это время с арабского языка переводятся труды мусульманских учёных, досконально изучивших работы древнегреческого математика. В XVI столетии методы великого исследователя природы использовал Галилей. Открытия, сделанные Архимедом, послужили фундаментом для развития средневековой механики.
Источник
Ïëàâàíèå òåë — ñîñòîÿíèå ðàâíîâåñèÿ òâåðäîãî òåëà, ÷àñòè÷íî èëè ïîëíîñòüþ ïîãðóæåííîãî â æèäêîñòü (èëè ãàç).
Îñíîâíàÿ çàäà÷à òåîðèè ïëàâàíèÿ òåë — îïðåäåëåíèå ðàâíîâåñèÿ òåëà, ïîãðóæåííîãî â æèäêîñòü, âûÿñíåíèå óñëîâèé óñòîé÷èâîñòè ðàâíîâåñèÿ. Íà ïðîñòåéøèå óñëîâèÿ ïëàâàíèÿ òåë óêàçûâàåò çàêîí Àðõèìåäà. Ðàññìîòðèì ýòè óñëîâèÿ.
Êàê èçâåñòíî, íà âñå òåëà, ïîãðóæåííûå â æèäêîñòü, äåéñòâóåò ñèëà Àðõèìåäà FA (âûòàëêèâàþùàÿ ñèëà), íàïðàâëåííàÿ âåðòèêàëüíî ââåðõ, îäíàêî âñïëûâàþò äàëåêî íå âñå. ×òîáû ïîíÿòü, ïî÷åìó îäíè òåëà âñïëûâàþò, à äðóãèå òîíóò, íåîáõîäèìî ó÷åñòü åùå îäíó ñèëó, äåéñòâóþùóþ íà âñå òåëà, — ñèëó òÿæåñòè Fò êîòîðàÿ íàïðàâëåíà âåðòèêàëüíî âíèç, ò. å. ïðîòèâîïîëîæíî FA. Åñëè òåëî îñòàâèòü âíóòðè æèäêîñòè â ñîñòîÿíèè ïîêîÿ, òî îíî íà÷íåò äâèãàòüñÿ â ñòîðîíó, â êîòîðóþ íàïðàâëåíà áîëüøàÿ èç ñèë. Ïðè ýòîì âîçìîæíû ñëåäóþùèå ñëó÷àè:
- åñëè àðõèìåäîâà ñèëà ìåíüøå ñèëû òÿæåñòè (FA< Fò), òî òåëî îïóñòèòñÿ íà äíî, ò. å. óòîíåò (ðèñ. à);
- åñëè àðõèìåäîâà ñèëà áîëüøå ñèëû òÿæåñòè (FA> Fò), òî òåëî âñïëûâåò (ðèñ. á);

3) åñëè àðõèìåäîâà ñèëà ðàâíà ñèëå òÿæåñòè (FA = Fò), òî òåëî îñòàíåòñÿ â ïîêîå. Ïîñëåäíåå óñëîâèå ÿâëÿåòñÿ óñëîâèåì ðàâíîâåñèÿ òåëà â æèäêîñòè:
FA = Fò.
Ðàâåíñòâî FA = Fò âûðàæàåò óñëîâèå ïëàâàíèÿ òåë: äëÿ òîãî, ÷òîáû òåëî ïëàâàëî, íåîáõîäèìî, ÷òîáû äåéñòâóþùàÿ íà íåãî ñèëà òÿæåñòè óðàâíîâåøèâàëàñü àðõèìåäîâîé (âûòàëêèâàþùåé) ñèëîé.
Óñëîâèþ ïëàâàíèÿ òåë ìîæíî ïðèäàòü äðóãóþ ôîðìó. Ïðåäñòàâèì àðõèìåäîâó ñèëó â âèäå:
FA = ρæ Væ g,
ãäå ρæ — ïëîòíîñòü æèäêîñòè, Vm — îáúåì æèäêîñòè, âûòåñíåííûé òåëîì, g — óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ. Ñèëó òÿæåñòè, äåéñòâóþùóþ íà òåëî, òîæå ìîæíî âûðàçèòü ÷åðåç îáúåì V è ïëîòíîñòü òåëà ρ:
Fò = mg = ρVg,
äå ò — ìàññà òåëà. Ïîäñòàâèì âûðàæåíèÿ FA = ρæ Væ g è Fò = mg = ρVg â ðàâåíñòâî FA = Fò:
ρVg = ρæ Væ g.
Ðàçäåëèâ îáå ÷àñòè ýòîãî ðàâåíñòâà íà g, ïîëó÷èì óñëîâèå ïëàâàíèå òåë â íîâîé ôîðìå:
ρV = ρæ Væ.
Èç ïîëó÷åííîãî ñîîòíîøåíèÿ ìîæíî âûâåñòè äâà âàæíûõ ñëåäñòâèÿ.
1. Äëÿ òîãî ÷òîáû òåëî ïëàâàëî, áóäó÷è ïîëíîñòüþ ïîãðóæåííûì â æèäêîñòü, íåîáõîäèìî, ÷òîáû ïëîòíîñòü òåëà áûëà ðàâíà ïëîòíîñòè æèäêîñòè.
2. Äëÿ òîãî ÷òîáû òåëî ïëàâàëî, ÷àñòè÷íî âûñòóïàÿ íàä ïîâåðõíîñòüþ æèäêîñòè, íåîáõîäèìî, ÷òîáû ïëîòíîñòü òåëà áûëà ìåíüøå ïëîòíîñòè æèäêîñòè.
Ïðè ρ > ρæ ïëàâàíèå òåë íåâîçìîæíî, òàê êàê â ýòîì ñëó÷àå ñèëà òÿæåñòè ïðåâûøàåò àðõèìåäîâó ñèëó, è òåëî òîíåò.

×òî áóäåò ïðîèñõîäèòü ñ òåëîì, ó êîòîðîãî ρ < ρæ, åñëè åãî ïîëíîñòüþ ïîãðóçèòü â æèäêîñòü?  ýòîì ñëó÷àå àðõèìåäîâà ñèëà áóäåò ïðåîáëàäàòü íàä ñèëîé òÿæåñòè, è ïîòîìó òåëî íà÷íåò ïîäíèìàòüñÿ ââåðõ. Ïîêà òåëî áóäåò äâèãàòüñÿ, îñòàâàÿñü ïîëíîñòüþ ïîãðóæåííûì â æèäêîñòü, àðõèìåäîâà ñèëà áóäåò îñòàâàòüñÿ íåèçìåííîé. Íî êàê òîëüêî òåëî äîñòèãíåò ïîâåðõíîñòè æèäêîñòè è ïîÿâèòñÿ íàä íåé, ýòà ñèëà (ïî ìåðå óìåíüøåíèÿ îáúåìà ÷àñòè òåëà, ïîãðóæåííîãî â æèäêîñòü) áóäåò ñòàíîâèòüñÿ âñå ìåíüøå è ìåíüøå. Âñïëûòèå ïðåêðàòèòñÿ òîãäà, êîãäà àðõèìåäîâà (âûòàëêèâàþùàÿ) ñèëà ñòàíåò ðàâíîé ñèëå òÿæåñòè. Ïðè ýòîì ÷åì ìåíüøåé ïëîòíîñòüþ (ïî ñðàâíåíèþ ñ ïëîòíîñòüþ æèäêîñòè) îáëàäàåò òåëî, òåì ìåíüøàÿ åãî ÷àñòü îñòàíåòñÿ âíóòðè æèäêîñòè.
Ïëàâàíèå ñóäîâ .
Ìàññà ñîâðåìåííûõ ñóäîâ äîñòèãàåò íåñêîëüêèõ äåñÿòêîâ òûñÿ÷ òîíí. Ïî÷åìó æå îíè íå òîíóò? Äåëî â òîì, ÷òî, íåñìîòðÿ íà îãðîìíóþ ìàññó, èõ ñðåäíÿÿ ïëîòíîñòü ïî-ïðåæíåìó ìåíüøå ïëîòíîñòè âîäû (áëàãîäàðÿ òîìó, ÷òî â êîðàáëÿõ ìíîãî ïóñòûõ ïîìåùåíèé). Ïðè ýòîì ñèëà òÿæåñòè, äåéñòâóþùàÿ íà ñóäíî, óðàâíîâåøèâàåòñÿ àðõèìåäîâîé (âûòàëêèâàþùåé) ñèëîé, è ñóäíî ïëàâàåò.
Ãëóáèíà, íà êîòîðóþ ïëàâàþùåå ñóäíî ïîãðóæàåòñÿ â âîäó, íàçûâàåòñÿ îñàäêîé ñóäíà. Ïðè ïîëíîé çàãðóçêå ñóäíà îíî íå äîëæíî ïîãðóæàòüñÿ â âîäó íèæå òàê íàçûâàåìîé ãðóçîâîé âàòåð-ëèíèè.
Âåñ âîäû, âûòåñíÿåìûé ñóäíîì ïðè ïîãðóæåíèè äî âàòåðëèíèè, ðàâíûé ñèëå òÿæåñòè, äåéñòâóþùåé íà ñóäíî ñ ãðóçîì, íàçûâàåòñÿ âîäîèçìåùåíèåì ñóäíà.
Åñëè èç âîäîèçìåùåíèÿ âû÷åñòü âåñ ñàìîãî ñóäíà, ïîëó÷èì ãðóçîïîäúåìíîñòü ñóäíà. Ãðóçîïîäúåìíîñòü ïîêàçûâàåò âåñ ãðóçà, ïåðåâîçèìîãî ñóäíîì.
Âîçäóõîïëàâàíèå .
Íà âñå òåëà â âîçäóõå (êàê è â æèäêîñòè) äåéñòâóåò âûòàëêèâàþùàÿ (àðõèìåäîâà) ñèëà. Äëÿ òåë, íàõîäÿùèõñÿ â âîçäóõå, îíà ðàâíà:
FA = ρâîçä V g,
ãäå ρâîçä — ïëîòíîñòü âîçäóõà.
Åñëè ýòà ñèëà îêàæåòñÿ áîëüøå ñèëû òÿæåñòè, äåéñòâóþùåé íà òåëî, òî òåëî âçëåòèò. Íà ýòîì îñíîâàíî âîçäóõîïëàâàíèå.
Ëåòàòåëüíûå àïïàðàòû, ïðèìåíÿåìûå â âîçäóõîïëàâàíèè, íàçûâàþò àýðîñòàòàìè (îò ãðå÷. aer — âîçäóõ, status — ñòîÿùèé). Íåóïðàâëÿåìûå àýðîñòàòû ñâîáîäíîãî ïîëåòà ñ îáîëî÷êîé, èìåþùåé ôîðìó øàðà, íàçûâàþò âîçäóøíûìè øàðàìè. Äëÿ èññëåäîâàíèÿ âåðõíèõ ñëîåâ àòìîñôåðû (ñòðàòîñôåðû) åùå íå òàê äàâíî ïðèìåíÿëèñü îãðîìíûå âîçäóøíûå øàðû — ñòðàòîñòàòû. Óïðàâëÿåìûå àýðîñòàòû (èìåþùèå äâèãàòåëü è âîçäóøíûå âèíòû) íàçûâàþò äèðèæàáëÿìè.
Âîçäóøíûé øàð íå òîëüêî ñàì ïîäíèìàåòñÿ ââåðõ, íî ìîæåò ïîäíÿòü è íåêîòîðûé ãðóç: êàáèíó, ëþäåé, ïðèáîðû. Äëÿ òîãî, ÷òîáû îïðåäåëèòü, êàêîé ãðóç ñïîñîáåí ïîäíÿòü âîçäóøíûé òàð, ñëåäóåò çíàòü åãî ïîäúåìíóþ ñèëó. Ïîäúåìíàÿ ñèëà âîçäóøíîãî øàðà ðàâíà ðàçíîñòè ìåæäó àðõèìåäîâîé ñèëîé è äåéñòâóþùåé íà øàð ñèëîé òÿæåñòè:
F = FA – Fò.
×åì ìåíüøå ïëîòíîñòü ãàçà, íàïîëíÿþùåãî âîçäóøíûé øàð äàííîãî îáúåìà, òåì ìåíüøå äåéñòâóþùàÿ íà íåãî ñèëà òÿæåñòè è òåì áîëüøå âîçíèêàþùàÿ ïîäúåìíàÿ ñèëà. Âîçäóøíûå øàðû ìîæíî íàïîëíÿòü ãåëèåì, âîäîðîäîì èëè íàãðåòûì âîçäóõîì. Õîòÿ ó âîäîðîäà ìåíüøå ïëîòíîñòü, ÷åì ó ãåëèÿ, âñå æå ÷àùå â öåëÿõ áåçîïàñíîñòè ïðèìåíÿþò ãåëèé (âîäîðîä — ãîðþ÷èé ãàç).
Ãîðàçäî ïðîùå îñóùåñòâèòü ïîäúåì è ñïóñê øàðà, íàïîëíåííîãî ãîðÿ÷èì âîçäóõîì. Äëÿ ýòîãî ïîä îòâåðñòèåì, íàõîäÿùèìñÿ â íèæíåé ÷àñòè øàðà, ðàñïîëàãàþò ãîðåëêó. Îíà ïîçâîëÿåò ðåãóëèðîâàòü òåìïåðàòóðó âîçäóõà, à çíà÷èò, è åãî ïëîòíîñòü è ïîäúåìíóþ ñèëó.
Ìîæíî ïîäîáðàòü òàêóþ òåìïåðàòóðó øàðà, ïðè êîòîðîé âåñ øàðà è êàáèíû áóäåò ðàâåí âûòàëêèâàþùåé ñèëå. Òîãäà øàð ïîâèñíåò â âîçäóõå, è ñ íåãî áóäåò ëåãêî ïðîâîäèòü íàáëþäåíèÿ.
Источник
Закон Архимеда
На тело, находящееся в жидкости или газе действует выталкивающая сила, которую называют силой Архимеда. Эта сила появляется в результате того, что давление в жидкости (газе) растет с увеличением глубины. Получается, что сила давления на тело в жидкости (газе) сверху вниз меньше, чем сила давления, направленная снизу вверх.
Сила Архимеда ($F_A$), действующая на тело, погруженное в жидкость или газ равна весу жидкости (газа) в объеме тела, находящегося в ней:
[F_A=rho Vg left(1right),]
где $rho $ – плотность жидкости (газа); $V$ – объем тела, находящийся в веществе; $g$ – ускорение свободного падения.
Сила Архимеда возникает только тогда, когда на жидкость (газ) действует сила тяжести. Так, в невесомости нет гидростатического давления и нет силы Архимеда.
И так, если тело погружено в жидкость, при этом оно находится в состоянии механического равновесия, то со стороны окружающей жидкости на тело действует выталкивающая сила гидростатического давления. Эта выталкивающая сила направлена вверх. Она проходит через центр масс жидкости, вытесненной телом (обозначим эту точку буквой А). Точку А называют центром плавучести тела. Положением точки плавучести определяют равновесие и устойчивость плавающего тела.
Плавание тел
Закон Архимеда объясняет вопросы, связанные с плаванием тел. Если тело находится в жидкости и оно предоставлено самому себе. Если вес тела больше, чем вес жидкости, которую оно вытесняет, то тело тонет. Если вес тела равен весу вытесненной им жидкости, то тело находится в равновесии внутри этой жидкости. Если вес тела меньше, чем вес вытесненной им жидкости, то тело всплывает, двигаясь к поверхности жидкости. Достигнув поверхности, тело плавает так, что его часть выступает над поверхностью жидкости. Плавающие тела, имеющие разные плотности имеют под поверхностью жидкости разные доли своего объема.
Если тело, погруженное в жидкость, имеет постоянную плотность ($rho $) во всех своих точках (тело однородно), то для определения состояния тела в жидкости можно сравнивать плотность вещества тела и плотность жидкости (${rho }_g$):
- $rho >{rho }_g$, тело тонет;
- $rho
- $rho ={rho }_g$ тело плавает (находится в равновесии) в жидкости.
Если тела являются неоднородными, то сравнивают среднюю плотность тела и плотность жидкости.
Равновесие тел в жидкости
При помощи закона Архимеда решают вопрос о равновесии тел, находящихся в жидкости. Для равновесия необходимо, чтобы вес тела равнялся весу вытесненной им жидкости, при этом центр плавучести А находился на одной вертикали с центром масс самого тела. При определении устойчивости равновесия выделяют два случая.
- Плавающее тело целиком погружено в жидкость. В этом случае при всяких поворотах и смещениях центр масс тела и центр плавучести сохраняют свое положение по отношению к телу. Равновесие будет устойчивым, если центр масс тела находится ниже центра плавучести.
- Плавающее тело погружено в жидкость частично. Его часть выступает над свободной поверхностью жидкости. При смещении тела из положения равновесия в этом случае изменяется форма вытесняемого телом объема жидкости. Положение центра плавучести относительно тела изменяется. В этом случае вводится понятие метацентра плавающего тела. Это точка, которая получается при пересечении вертикальной оси симметрии тела и линии действия выталкивающей силы. Если метацентр ниже центра масс тела, то положение равновесия не устойчиво.
Примеры задач с решением
Пример 1
Задание. Объясните, что происходит с пузырьком газа, оказавшимся в толще воды.
Решение. Пузырек газа всплывает в толще воды, так как сила выталкивания $F_A=rho Vg $, действующая на него, равна весу воды объема пузырька. При этом такой объем воды весит значительно больше, чем весит газ в пузырьке. Двигаясь наверх пузырек, испытывает все меньшее давление ($p$), так как давление столба жидкости зависит от его высоты ($h$):
[p=rho gh left(1.1right).]
Так как внешнее давление на пузырек уменьшается, от он расширяется, уравновешивая внутреннее давление газа с внешним давлением на его стенки со стороны воды. При увеличении объема пузырька увеличивается, действующая на него сила Архимеда. Скорость движения пузырька к поверхности воды увеличивается.
Пример 2
Задание. Каково отношение плотности материала шарика ($rho $) к плотности жидкости (${rho }_g$), если шарик всплывает в этой жидкости с постоянной скоростью? Отношение веса (P) шарика к силе сопротивления ($F_s$) движению шарика в жидкости равно $frac{P}{F_s}=frac{1}{2}$.
Решение. Рассмотрим силы, действующие на шарик (рис.1), запишем второй закон Ньютона для них, учитывая, что движение равномерное, то есть $a=0.$
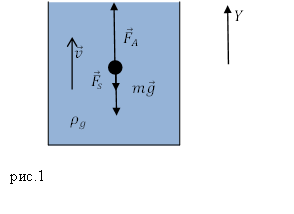
[moverline{g}+{overline{F}}_s+{overline{F}}_A=0left(2.1right).]
Запишем проекцию уравнения (2.1) на ось Y:
[-mg-F_s+F_A=0 left(2.2right).]
Массу шарика выразим как:
[m=rho V left(2.3right),]
где $V$ – объем шарика.
Сила Архимеда, заставляющая шарик всплывать равна:
[F_A={rho }_gVg left(2.4right).]
Вес тела равен:
[P=mg left(2.5right).]
Выразим силу сопротивления из уравнения (2.2), получим:
[F_s=F_A-mgleft(2.6right).]
Разделим правую и левую части (2.6) на вес тела, имеем:
[frac{F_s}{P}=frac{F_A-mg}{mg}=frac{F_A}{mg}-1 left(2.7right).]
Используем выражения (2.3)и (2.4)преобразуем формулу (2.7) к виду:
[frac{F_s}{P}=frac{{rho }_gVg}{rho Vg}-1= frac{{rho }_g}{rho }-1left(2.8right).]
Из (2.8) получим искомое отношение:
[frac{F_s}{P}+1= frac{{rho }_g}{rho }to frac{rho }{{rho }_g}=frac{1}{frac{F_s}{P}+1}=frac{1}{2+1}=frac{1}{3}.]
Ответ. $frac{rho }{{rho }_g}=frac{1}{3}$ плотность шарика в три раза меньше, чем плотность жидкости.
Читать дальше: фаза колебаний.
Источник
